Вероятности и/или одды (шансы за и против) - два способа выражения для степени правдоподобия случайного события

Вероятность можно определить как меру правдоподобия случайного события A, выражаемую в долях от единицы:

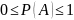
Другой способ выражать степень правдоподобия события A - посредством оддов, соотнося вероятность события A с вероятностью противоположного события 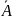(не A).

«Одды» (шансы за и против)

«Одды» или шансы за и против события A определяются как отношение вероятности этого события к вероятности противоположного события :

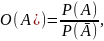
где 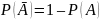. Одды или шансы за и против события A не определены, когда , ибо деление на ноль – запрещенная операция.

Понятие оддов (шансов за и против) нам знакомо из курсов по генетике. Знаменитое менделевское отношение A- : aa = 3 : 1 суть одды в пользу доминантного фенотипа против рецессивного. В терминах вероятностей это будут:

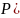и .

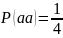Независимые события

Одним из фундаментальнейших понятий в теории вероятностей является понятие независимости случайных событий.

По определению два случайных события A и B являются независимыми, когда вероятность их совмещения (AB), т.е. их одновременного осуществления равна произведению вероятностей каждого из этих событий по отдельности:

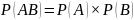
Отношение оддов

Одной из мер зависимости между двумя случайными событиями может служить величина, называемая отношением оддов.

Отношение оддов OR (Odds Ratio) для двух случайных событий A и B есть отношение шансов за и против события A к шансам за и против события B:

Напомним, что 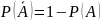и .

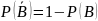Условные вероятности

Фактически все показатели точности, прогностичности и согласованности клинико-лабораторного диагностического теста являются условными вероятностями и функциями от них.

По определению, условная вероятность события A при условии, что (уже) произошло событие B, есть результат деления вероятности совмещения обоих этих событий P(AB) на вероятность происшедшего события B:

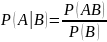
В формулах для обозначения условных вероятностей используется символ “|” - вертикальная черта. Читается и произносится как: «при условии, что» (или просто «при»).

Выражение читается как: «вероятность случайного события A при условии, что произошло событие B» (или «при условии, что утверждение B верно»).

«Заблуждение обвинителя»

Принципиально важно осознавать, что условные вероятности необращаемы. А именно: вероятность события A при условии, что осуществилось событие B, не есть вероятность события B при условии, что произошло событие A:

Например, чувствительность клинико-лабораторного диагностического теста, т.е. вероятность получить положительный результат у субъекта с данной болезнью не равна предсказательной (апостериорной) вероятности наличия болезни у субъекта с положительным результатом теста:

При проверке статистических гипотез важно помнить, что вероятность получить наблюдаемые данные D при условии, что верна нулевая гипотеза H₀, не есть апостериорная вероятность гипотезы H₀ после получения экспериментальных данных:

В судебной генетике подобные заблуждения называют «заблуждением обвинителя (прокурора)». Вероятность наблюдать у заподозренного субъекта ДНК-профиль (генотип) G, идентичный генотипу ДНК-улики при условии, что заподозренный невиновен (I – innocent), не есть вероятность того, что заподозренный невиновен, если у него обнаружен данный генотип:

Связь между подобными условными вероятностями устанавливает теорема Бейза.