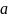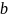- •А.В. Тишков, н.Н. Хромов-Борисов, а.В. Комашня, ф.Ю. Марченкова, е.М. Семенова, н.И. Эюбова, е.А. Делакова, а.В. Быхова
- •Пояснительная записка
- •Введение
- •Статистический анализ – единственный путь оценки и сравнения клинико-лабораторных диагностических тестов
- •Основные типы клинико-лабораторных тестов1
- •Клинико-лабораторные диагностические исследования2
- •«Золотой стандарт» или Эталон сравнения
- •Необходимые сведения из теории вероятностей и математической статистики3
- •Вероятности и/или одды (шансы за и против) - два способа выражения для степени правдоподобия случайного события
- •«Одды» (шансы за и против)
- •Независимые события
- •Отношение оддов
- •Условные вероятности
- •«Заблуждение обвинителя»
- •Формула Бейза: вероятность причин, гипотез, или обратные или предсказательные вероятности
- •Формула Бейза в терминах оддов и правдоподобий
- •Популяция и выборка Определение понятия «популяция»
- •Важнейшее требование к популяции и к выборке - однородность4
- •Всё познается в сравнении
- •Требования к проведению проверки качества клинико-лабораторного диагностического теста
- •Эталонный клинико-лабораторный диагностический тест
- •Диагностическая таблица перекрестной классификации 2×2
- •Типы показателей качества диагностических тестов
- •Показатели предсказательной способности пклдт, т.Е. Способности его положительных или отрицательных результатов предсказывать наличие или отсутствие диагностируемой болезни
- •Отношения правдоподобий
- •Представление отношений правдоподобий в терминах оддов (шансов за и против)
- •Показатели согласованности
- •Отношение оддов
- •Коэффициент каппа Коуэна
- •Наблюдаемые численности исходов
- •Статистическое оценивание
- •Два основных типа статистических оценок
- •Основная логика статистического оценивания: точечные оценки
- •Основная логика статистического оценивания: интервальные оценки
- •Доверительные интервалы
- •Точность и надежность статистических оценок
- •Надежность доверительных интервалов (ди)
- •Точечные статистические оценки вероятностей наблюдать положительные или отрицательные результаты пклдт у субъектов с болезнью или без нее
- •Идеальный и бесполезный тесты в терминах Se и Sp
- •Возможные словесные интерпретации для градаций Se и Sp
- •Статистическая интерпретация ди для Se и Sp
- •Статистическая значимость Se и Sp
- •Точечные статистические оценки предсказательных вероятностей наличия или отсутствия болезни у субъектов с положительными или отрицательными результатами пклдт
- •Идеальный и бесполезный тесты в терминах ppv и npv
- •Точечные статистические оценки для отношений правдоподобий
- •Идеальный и бесполезный тесты в терминах lr
- •Статистическая интерпретация ди для lr
- •Статистическая значимость lr
- •Показатели согласованности Отношение оддов
- •Статистическая интерпретация ди для or
- •Статистическая значимость or
- •Словесная интерпретация градаций для or5
- •Коэффициенты каппа Коуэна
- •Статистическая интерпретация ди для κC
- •Статистическая значимость κC
- •Словесная интерпретация градаций коэффициента каппа Коуэна
- •Исследования типа «случаи – контроли»
- •Наблюдаемые численности исходов при формировании выборок по схеме «случаи-контроли»
- •Оценки предсказательных ценностей положительных и отрицательных результатов теста в схеме «случаи» и «контроли» Согласно теореме Бейза:
- •Точечные статистические иоценки предсказательных вероятностей наличия или отсутствия болезни у субъектов с положительными или отрицательными результатами пклдт в схеме «случаи» и «контроли»
- •Приложение
- •Дополнительные показатели точности и информативности клинико-лабораторных диагностических тестов Дополнительные показатели точности
- •Дополнительные показатели информативности
- •Литература
- •Построение доверительных интервалов для основных показателей согласованности, точности и информативности клинико-лабораторного диагностического теста
- •Доверительные интервалы для показателей точности и информативности при формировании общепопуляционной выборки
- •Доверительные интервалы для ppv и npv при формировании выборок по схеме «случаи-контроли»
- •Доверительные границы для разности долей
- •Частотнический подход
- •Бейзовский подход
- •Доверительный интервал для коэффициента каппа Коуэна
- •Доверительный интервал для отношения оддов
Наблюдаемые численности исходов
Проверяемый клинико-лабораторный диагностический тест (ПКЛДТ) |
Эталон сравнения |
Всего |
||
Результат: |
||||
[+] |
[-] |
|||
Результат: |
[+] |
|
|
|
[-] |
|
|
|
|
Всего |
|
|
|
|
Статистическими оценками разрешающей и предсказательной способностей ПКЛДТ являются соответствующие наблюдаемые частоты.
Статистическое оценивание
Одной из основных задач статистики является статистическое оценивание числовых характеристик (параметров) обследуемой популяции.
Цель – по возможности точно и надежно определить (вычислить) значение той или иной числовой характеристики (параметра).
Материалом для этого служат имеющиеся статистические данные.
При оценивании параметров на основе варьирующих данных нельзя ограничиваться одним числом.
Обязательно нужны еще оценки их варьирования.
Два основных типа статистических оценок
Точечное оценивание – оценка одним числом.
Интервальное оценивание – оценка интервалом.
Для интервального оценивания в статистике используются Доверительные Интервалы.
Доверительный интервал — это такой интервал, который содержит (накрывает) оцениваемый параметр с заданной вероятностью.
Такая вероятность называется Доверительной Вероятностью или Уровнем Доверия.
Уровень Доверия выбирается исследователем.
Основная логика статистического оценивания: точечные оценки
В биомедицинских исследованиях обычно вероятности P (или иные параметры) нам неизвестны.
Мы их оцениваем по наблюдаемым численностям.
Например, разумной и интуитивно понятной точечной оценкой для распространенности болезни по данным общепопуляционного (одномоментного поперечно-срезового) исследования может служить наблюдаемая частота
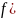
т.е.
доля числа больных
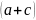 ,
выявленных золотым стандартом, от общего
числа n
обследованных.
,
выявленных золотым стандартом, от общего
числа n
обследованных.
Основная логика статистического оценивания: интервальные оценки
Легко представить, что если мы многократно повторим извлечение выборок из данной популяции, то наблюдаемые частоты неизбежно будут варьировать.
Поэтому задача математиков – вывести математический закон (вероятностное распределение), которому подчиняется варьирование этой частоты.
Если
такой закон найден, то тогда можно
получить доверительные интервалы (ДИ)
для оценки распространенности болезни
с заданной доверительной вероятностью
 .
.
Доверительные интервалы
Доверительный Интервал (ДИ) есть такой интервал, который с заданной (доверительной) вероятностью накрывает искомое оцениваемое значение параметра.
Синонимы: Интервал Доверия или Интервал Накрытия.
Принципиально важно понимать, что ДИ является случайным.
Это означает, что от опыта к опыту его границы будут колебаться, варьировать.
Точность и надежность статистических оценок
Чем ýже ДИ, тем оценка точнее.
Чем больше доверительная вероятность , тем оценка надежнее.
Однако ДИ с доверительной вероятностью 100% - бессмыслен.
Например, 100%-й ДИ для доли будет содержать все значения в границах от 0 до 1: [0, 1].