14. Анализ устойчивости нелинейных систем методом гармонической линеаризации.

На рис.10.2 приведена схема нелинейной системы, для анализа которой можно воспользоваться методом гармонической линеаризации

Рис.10.2 Структурная схема нелинейной системы

В этой схеме входной сигнал x(t) = Asint - гармонический, а после нелинейного элемента НЭ включен фильтр нижних частот (ФНЧ) с передаточной функцией W_л(p).

При гармоническом входном сигнале x(t) = Asint = Asin, где =t сигнал y на выходе НЭ будет периодическим, но не гармоническим, так как зависимость y=f(x) нелинейная. Периодические сигналы можно представить рядом Фурье

y = f(x) = q(A)Asin + q₁(A)Acos + y_вч ,

где q(A) и q₁(A) - коэффициенты ряда Фурье для первых гармоник синуса и косинуса, которые определяются по формулам:

, (10.1) , (10.2)

где y - сигнал на выходе НЭ при изменении фазы  входного сигнала x от - до ,

y_вч - высокочастотные составляющие (высшие гармоники) в сигнале y.

Так как на выходе НЭ включен фильтр нижних частот, который не пропускает на выход высшие гармоники сигнала y, тогда на его выходе будут присутствовать только первые гармоники в сигнале y, т. е.

y_вых = q(A)Asin + q₁(A)Acos.

Так как , откуда , здесь - символ дифференцирования.

Следовательно .

От гармонических сигналов x и y перейдем к комплексным сигналам путем замены p=j , тогда получим:

Y(jt) = X(jt)[q(A) + jq₁(A)] (10.3)

Это соотношение устанавливает связь между первой гармоникой комплексных сигналов на входе и выходе НЭ, для которого введем понятие нелинейного ККП

W_Н(A) = q(A) + jq₁(A) (10.4)

тогда Y(jt) = X(jt)W_Н(A).

Определим коэффициенты q(A) и q₁(A) для нелинейных элементов, характеристики которых приведены на рис.10.1.в и 10.1.з.

Для идеального ограничителя (рис.10.1.в) получим:

15. Особенности работы импульсных, дискретных и цифровых систем управления, их достоинства и недостатки.

Дискретные системы – это системы, содержащие элементы, которые преобразуют непрерывный сигнал в дискретный. В дискретных системах сигналы описываются дискретными функциями времени.

Квантование - процесс преобразования непрерывного сигнала в дискретный.

На рис.8.1 приведена структурная схема замкнутой цифровой системы управления.

Рис 8.1 Структурная схема замкнутой цифровой системы управления

В состав этой схемы входят следующие блоки:

АЦП - аналого-цифровые преобразователи, преобразующие непрерывные сигналы x(t), y(t) в последовательность чисел x(n), y(n), соответствующих значению сигналов x(t), y(t) в определенные моменты времени (см. рис. 8.2),

ЦАП - цифро-аналоговый преобразователь, преобразующий поступающую на его вход последовательность чисел u(n) в непрерывный сигнал u(t),

ЭВМ - электронно-вычислительная машина, обрабатывающая по определенной программе поступающие на ее входы числа x(n) и y(n).

ОУ - объект управления, на который действует управляющее воздействие u(t).

Состояние объекта характеризуется его выходным сигналом y(t).

Сигналы x(n), u(n) и y(n) называют цифровыми сигналами.

Для нормальной работы цифровых систем управления отсчеты из непрерывных сигналов x(t) и y(t) должны осуществляться с частотой F_д, величина которой должна быть больше определенной частоты, определяемой из теоремы отсчетов Котельникова-Найквиста.

Теорема отсчетов гласит: непрерывный сигнал может быть точно восстановлен по его отсчетам, если отсчеты берутся с частотой F_д>2F_макс, где F_макс - максимальная частота спектра непрерывного сигнала.

Частоту отсчетов из сигнала F_д называют обычно частотой дискретизации.

На рис.8.2 приведена временная диаграмма непрерывного сигнала x(t) и отсчеты из него x(n), взятые через период дискретизации T, связанный с частотой дискретизации соотношением T=1/F_д.

Современные системы автоматического управления строятся в основном как цифровые системы. Это объясняется тем, что цифровым системам присущи определенные достоинства:

• высокая точность управления,

• возможность управления по сложным алгоритмам, включающим адаптацию, самонастраивающиеся процедуры, контроль и диагностику неисправностей,

• высокая стабильность параметров,

• возможность оперативно изменять алгоритмы и программы управления,

• высокая технологичность при изготовлении и идентичность характеристик различных экземпляров цифровых систем управления.

К недостаткам цифровых систем следует отнести:

• ограниченный частотный диапазон обрабатываемых сигналов,

• высокая стоимость цифровых систем управления даже при простых (примитивных) алгоритмах управления объектами.

Из-за указанных недостатков реальные системы управления строятся как на аналоговой, так и на цифровой элементной базе.

Рис.8.2 Временные диаграммы непрерывного x(t) и цифрового x(n) сигналов

Дискретная система автоматического управления будет импульсной, если в системе наблюдается квантование сигнала по времени. При квантовании по времени квантованный сигнал состоит из последовательности дискрет квантуемого сигнала. Каждую дискрету можно рассматривать как мгновенное значение сигнала в момент квантования и интерпретировать как импульс нулевой длительности. Такой импульс физически не наблюдаем.

Для того чтобы квантованный сигнал можно было бы физически наблюдать и преобразовывать, мгновенные значения квантуемого сигнала накладываются на физические импульсы конечной длительности. В результате в импульсной системе квантованный сигнал физически представлен последовательностью импульсов, несущих информацию о мгновенных значениях квантуемого сигнала в моменты квантования. Название импульсная система обусловлено последним обстоятельством.

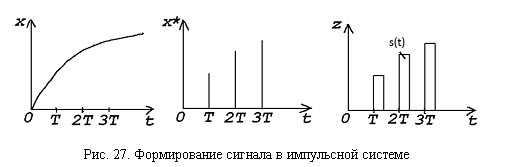
Графики на рис. 27 показывают образование импульсного сигнала в импульсной системе. Квантуемый сигнал x(t) подвергается квантованию по времени и образуется квантованный сигнал x*(t), который можно описать решетчатой функцией квантуемого сигнала

Значения дискрет квантованного сигнала накладываются на импульсы определенной формы s(t) и конечной длительности. В результате формируется последовательность импульсов z(t) с периодом следования T, несущая информацию о квантуемом сигнале.

Отличительной особенностью импульсной системы является преобразование непрерывного сигнала x(t) в последовательность импульсов z(t). Поэтому для описания импульсной системы в ее структуру вводят импульсное звено, которому и приписывают описание этого процесса. Остальные компоненты импульсной системы специфических свойств не имеют, они рассматриваются как непрерывная часть системы (т.е. совокупность элементов с непрерывными характеристиками преобразования) и могут быть описаны с использованием методов теории обыкновенных линейных систем.

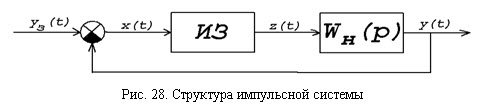
Обобщенная структура импульсной системы, составленная на основе описанного подхода, приведена на рис. 28. Импульсному звену ИЗ приписывается преобразование непрерывного сигнала x(t) в последовательность импульсов z(t), которая поступает на непрерывную часть импульсной системы с передаточной функцией W_н(p).

В исследуемой системе импульсное звено может быть включено в любой части системы. Путем преобразования структуры исследуемой системы ее всегда можно свести к структуре, представленной на рис. 28. При этом математическое описание импульсной системы сводится к математическому описанию функции преобразования для импульсного звена. Решение последней задачи будет зависеть от способа наложения информации квантованного сигнала на несущие импульсы.