12. Методы линеаризации нелинейных моделей.

На рис.10.2 приведена схема нелинейной системы, для анализа которой можно воспользоваться методом гармонической линеаризации

Рис.10.2 Структурная схема нелинейной системы

В этой схеме входной сигнал x(t) = Asint - гармонический, а после нелинейного элемента НЭ включен фильтр нижних частот (ФНЧ) с передаточной функцией W_л(p).

При гармоническом входном сигнале x(t) = Asint = Asin, где =t сигнал y на выходе НЭ будет периодическим, но не гармоническим, так как зависимость y=f(x) нелинейная. Периодические сигналы можно представить рядом Фурье

y = f(x) = q(A)Asin + q₁(A)Acos + y_вч ,

где q(A) и q₁(A) - коэффициенты ряда Фурье для первых гармоник синуса и косинуса, которые определяются по формулам:

, (10.1) , (10.2)

где y - сигнал на выходе НЭ при изменении фазы  входного сигнала x от - до ,

y_вч - высокочастотные составляющие (высшие гармоники) в сигнале y.

Так как на выходе НЭ включен фильтр нижних частот, который не пропускает на выход высшие гармоники сигнала y, тогда на его выходе будут присутствовать только первые гармоники в сигнале y, т. е.

y_вых = q(A)Asin + q₁(A)Acos.

Так как , откуда , здесь - символ дифференцирования.

Следовательно .

От гармонических сигналов x и y перейдем к комплексным сигналам путем замены p=j , тогда получим:

Y(jt) = X(jt)[q(A) + jq₁(A)] (10.3)

Это соотношение устанавливает связь между первой гармоникой комплексных сигналов на входе и выходе НЭ, для которого введем понятие нелинейного ККП

W_Н(A) = q(A) + jq₁(A) (10.4)

тогда Y(jt) = X(jt)W_Н(A).

Определим коэффициенты q(A) и q₁(A) для нелинейных элементов, характеристики которых приведены на рис.10.1.в и 10.1.з.

Для идеального ограничителя (рис.10.1.в) получим:

13. Анализ поведения нелинейных систем на фазовой плоскости.

Метод фазовой плоскости применяется для анализа нелинейных систем, порядок которых не выше второго. На плоскости с координатами   и , где  – ошибка системы или какой-либо другой сигнал, строится траектория движения системы. Плоскость и траекторию движения  систем   называют  фазовыми.  По  характеру фазовой  траектории  оценивается  качество  работы  системы.

Метод фазовой плоскости используется для исследования нелинейных САУ, линей­ная часть которых с достаточной для решения практических задач точностью может быть описана диффе­ренциальным уравнением второго порядка.

Фазовой плоскостью называется плоскость, на кото­рой изображается изменение какой-либо переменной ве­личины   в функции скорости ее изменения: . Оси времени на фазовой плоскости нет, но каждому моменту времени соответствует определенная точка (изображающая точка), абсцисса и ордината  которой равны соответственно значению сигнала и скорости его изменения в данный момент времени. При изменении времени изображающая точка перемещается по определенной траектории, называемой фазовой траекторией. Определим выражение фазовой траектории для сигнала  , представляющего собой незатухающие гармониче­ские колебания с амплитудой  и частотой   (рис. 8.6, а): .                                                           (8.1) Скорость изменения такого сигнала равна: .                                                   (8.2) Выражая из уравнений (8.1) и (8.2)       и    , на основании основного тригонометрического тождества получим: .                                                         (8.3) Следовательно, незатухающие гармонические колеба­ния изображаются на фазовой плоскости в виде эллипса (рис. 8.6, б) с полуосями А и  . При изменении времени изображающая точка, будет перемещаться вдоль эллипса по часовой стрелке с периодом колебания  . Для различных амплитуд  А при заданной частоте   можно построить семейство таких эллипсов, вложенных один в другой (рис. 8.6, в). Совокупность фазовых траекторий нелинейной системы, соответствующих различным значения ее параметров или начальных условий, называется фазовой картиной  (фазовым портретом). 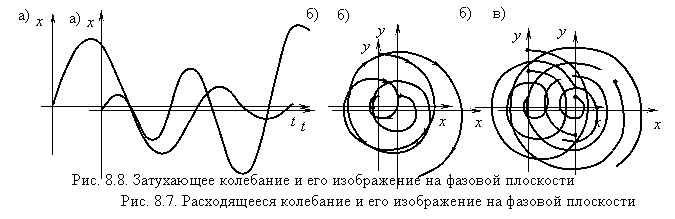В случае расходящегося колебательного процесса (рис. 8.7, а) амплитуда колебаний увеличи­вается и соответствующая такому процессу  фазовая траектория  бу­дет иметь вид расходящейся логарифмической спирали (рис. 8.7, б). Наоборот,  затухающий   колебательный   процесс (рис. 8.8, а) на фазовой плоскости изображается в виде логарифмической спирали, сходящейся к началу коорди­нат (рис. 8.8, б). Фазовые портреты, соответствующие различным значениям начальных условий для таких процессов приведены соответственно на рис. 8.7, в и рис. 8.8, в. Таким образом, по виду фазовой траектории можно наглядно судить об устойчивости си­стемы.