Третий план

Склад	Севооборот						Запасы, тонн
	Vj Ui	№1	№2	№3	№4	№5
		4	2	3	1	-1
№1	0	4	2 150	3 50	1	0	200
№2	-1	3 100	6	2 50	5	0	150
№3	1	6	3	4 50	2 75	0 125	250
Потребность, тонн		100	150	150	75	125	600

3. Алгоритм решения транспортной задачи в еxcel

3.1. Транспортная задача на минимум Задача 2

В хозяйстве силосная масса заготовлена в трех траншеях в следующем объеме: в первой траншее – 500 т, во второй – 850 т, в третьей – 600 т.

Сезонная потребность ферм в силосе следующая: первой ферме требуется – 400 т, второй – 550 т, третьей – 700 т и четвертой – 300 т.

Оптимизировать план перевозок силоса от траншей к животноводческим фермам, чтобы суммарные издержки на доставку были бы минимальными. Себестоимость 1 т-км составляет в среднем по хозяйству 5 руб.

Расстояние между траншеями и фермами.

Фермы	Траншеи
	Первая	Вторая	Третья
Первая	3	8	5
Вторая	7	5	6
Третья	2	7	4
Четвертая	9	8	4

-10-

Решение

Оформим в EXCEL следующую таблицу и введем в нее зависимости:

B3=СУММ (С3:F3)

B4=СУММ (С4:F4)

B5=СУММ (С5:F5)

B6=СУММ (С6:F6)

С6=СУММ(С3:С5)

D6=СУММ(D3:D5)

E6=СУММ(E3:E5)

F6=СУММ(F3:F5)

В12=СУММ(С12:F12)

С12=СУММПРОИЗВ(С3:C5;C9:C11)

D12=СУММПРОИЗВ(D3:D5;D9:D11)

E12=СУММПРОИЗВ(E3:E5;E9:E11)

F12=СУММПРОИЗВ(F3:F5;F9:F11)

	A	B	C	D	E	F
1			Пункты назначения
2	Пункты отправления	Всего:	Ферма 1	Ферма2	Ферма3	Ферма4
3	Траншея 1	0
4	Траншея 2	0
5	Траншея 3	0
6	Всего:	0	0	0	0	0
7	Потребность:	1950	400	550	700	300
8	Пункты отправления	Наличие:	Затраты на доставку 1 тонны
9	Траншея 1	500	15	21	10	45
10	Траншея 2	850	40	25	35	40
11	Траншея 3	600	25	30	20	20
12	Затраты всего (ЦФ)	0	0	0	0	0

У 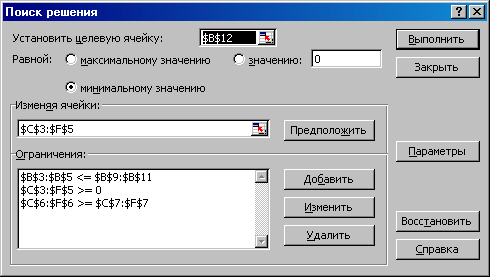становим курсор в ячейке В12 и дадим команду Сервис/Поиск решения.

В диалоговом окне установим целевую ячейку $В$12 равной минимальному значению (цель решения задачи – уменьшение всех транспортных расходов). Установим диапазон изменяемых ячеек $С$3:$F$5 (объемы перевозок от каждой траншеи к каждой ферме).

-11-

Щ 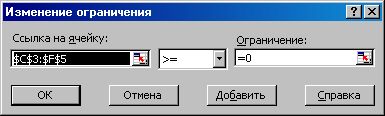елчком по кнопке Добавить введем следующие ограничения:

1) $С$3:$F$5>=0 (объем перевозок не может быть отрицательным);

2) $B$3:$B$5<=$B$9:$B$11 (поставки силоса не могут превышать его наличия в траншее);

3) $C$6:$F$6>=$C$7:$F$7 (поставки силоса на каждую ферму не могут быть меньше потребности в нем).

Щелкнем по кнопке Параметры и установим в открывшемся окне флажок Линейная модель. Затем нажимаем кнопку Выполнить в диалоговом окне Поиск решения.

П 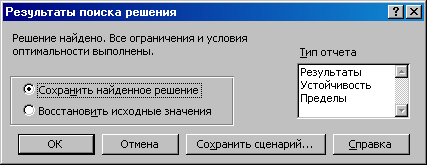олучен оптимальный план перевозок с наименьшими затратами. Удовлетворены все ограничения. Результаты представлены в следующей таблице:

		Пункты назначения
Пункты отправления	Всего:	Ферма 1	Ферма2	Ферма3	Ферма4
Траншея 1	500	0	0	500	0
Траншея 2	850	100	550	200	0
Траншея 3	600	300	0	0	300
Всего:	1950	400	550	700	300
Потребность:	1950	400	550	700	300
Пункты отправления	Наличие:	Затраты на доставку 1 тонны
Траншея 1	500	15	21	10	45
Траншея 2	850	40	25	35	40
Траншея 3	600	25	30	20	20
Затраты всего (ЦФ)	43250	11500	13750	12000	6000

По оптимальному плану на первую ферму необходимо доставить силос из второй траншеи (100 т) и третьей (300 т). Потребность второй фермы (550 т) полностью удовлетворяется запасами силоса из второй траншеи, а четвертой – из третьей траншеи (300 т). Весь силос из первой траншеи (500 т) и остатки силоса из второй траншеи (200 т) рекомендуется перевезти на третью ферму, тогда ее потребность будет покрыта. Общая стоимость перевозок при этом будет минимальной и составит 43250 руб.

В диалоговом окне Результаты поиска решения можно выбрать отчеты трех типов. Проведем анализ устойчивости результатов полученного оптимального решения.

Отчет по устойчивости состоит из двух таблиц. В первой показаны результаты решения и дана нормированная стоимость, то есть двойственные оценки, показывающие, как изменится целевая функция при принудительном включении в оптимальное решение не вошедших в него переменных.

-12-

Так, например, при перевозке силоса из первой траншеи на вторую и четвертую фермы транспортные издержки возрастут с каждой тонной перевезенного груза на 21 и 35 руб. соответственно. Затраты возрастут на 5 руб. если вывезти хотя бы одну тонну силоса со второй траншеи на четвертую ферму и на 20 руб. при перевозке силоса из третьей траншеи на вторую ферму.

Х 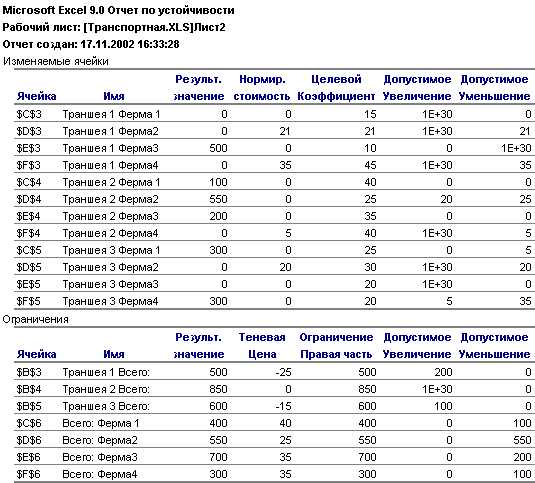отя в оптимальном решении не рекомендуется перевозить силос с первой траншеи на первую ферму, а также с третьей траншеи на третью ферму, нормированная стоимость для этих переменных равна нулю. Это означает, что у данной задачи есть альтернативные решения, то есть включение данных переменных в оптимальный план перевозок не приведет к увеличению затрат.

Графы «Допустимое увеличение» и «Допустимое уменьшение» показывают, в каких пределах могут изменяться удельные транспортные издержки, чтобы структура полученного оптимального решения не изменилась.

Вторая таблица отчета по устойчивости содержит сведения о выполнении ограничений задачи. Теневая цена показывает, как изменится целевая функция при увеличении объема правой части ограничений на единицу. Так, если бы наличие силоса в первой и третьей траншее было бы больше на 1 тонну, то суммарные транспортные издержки уменьшились соответственно на 25 и 15 руб. Это обусловлено тем, что затраты на перевозку силоса с этих траншей на любую ферму несколько ниже, чем при перевозке со второй траншеи.

Допустимое увеличение и уменьшение показывают, в каких пределах может изменяться объем ограничений, чтобы структура полученного оптимального решения не изменилась.

-13-