31. Аналитические показатели рядов динамики. Способы их расчета

Для характеристики развития явления исп-ся система показателей: абсол. приросты (∆_y), темпы роста (T_y), темпы прироста (T_∆), абсол. значение 1%прироста (A).

В завис-ти от задачи исслед-ния, абсол. приросты, темпы роста и темпы прироста м.б. исчислены с перемен. базой сравнения (цепные) и постоян. базой сравнения (базисные).

Абсол. прирост–разность между послед. уровнем ряда и предыдущ. или базисным. Цепной: ∆_y=y_i - y_i-1 Базисный: ∆_y=y_i - y₀. Абсол. прирост показывает на сколько ед. уровень одного периода > или < (отрицательный знак) уровня др. периода. Сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики.

Темп роста–относит. пок-ль, характериз. интенсивность развития явления. Равен отн-нию изучаемых уровней и выражается в % или коэф-тах.

Цепной: T_y = y_i / y_i-1 *100% Базисный: T_y= y_i / y₀ *100%. T_y всегда положительная величина.

Произведение цепн. темпов роста = базисн. темпу роста и наоборот: частное от деления базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

Темп прироста показывает на сколько %-ов изменился изучаемый пок-ль в ед. времени. Измеряется:1)отн-ние абсол. прироста к предыдущ. или базисн. уровню.

Цепной:T_∆=∆_y/y_i-1 *100% Базисный: T_∆=∆_y/ y₀*100%; T_∆=((y_i-y₀)/y₀)*100%

Между показателями темпа прироста и темпа роста имеется взаимосвязь:

T∆ =Ty −100% (при выражении темпа роста в процентах); T∆ =Ty −1(при выражении темпа роста в коэффициентах).

Темп наращивания, который измеряет наращивание во времени экономического потенциала. Вычисляются темпы наращивания Тн делением цепных абсолютных приростов ∆y на уровень, принятый за постоянную базу

сравнения, у_0. Тн = ∆у : у₀

Абсол. значение 1-го %-та прироста–Отношение цепного абсолютного прироста к темпу прироста, выраженному в %-ах. А=∆_у /Т_∆

32. Способы расчета среднего уровня в рядах динамики

Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста и др.

Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.

В интервальных рядах динамики с равными интервалами средний уровень 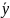определяется делением суммы уровней 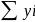, на их число n: = .

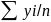В интервальных рядах динамики с неравными интервалами средний уровень рассчитывается по формуле средней арифметической взвешенной:

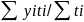= , где yi – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени t.

В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле средней хронологической:

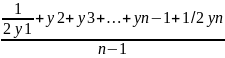= , где n – число дат.

В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней арифметической взвешенной: =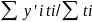 , где yi′ – средняя величина признака между двумя датами, t –

количество дней (месяцев) между смежными датами.