26. Способы отбора единиц в выборочную совокупность.

Для того чтобы по выборке можно было сделать вывод о св-вах генеральной сов-сти, выборка д б репрезентативной. Т.е. она должна наиболее полно и адекватно представлять св-ва генер сов-сти. Репрезентативность выборки м б обеспечена только при объективности отбора данных.

Возможны 3 способа отбора:1)Случайный отбор;2)Отбор по определенной схеме;3)Сочетание первого и второго способов.Если отбор в соотв-вии с принятой схемой произв-ся из генер сов-сти, предварительно разделенной на типы или страты, то выборка наз-ся типической или стратифицированной. Если единицы отбора являются серия единиц (серийная выборка).Различают два вида отбора -повторный и бесповторный. Первый соответствует схеме «возвращенного шара»: после отбора какой-либо

единицы она возвращается в генеральную совокупность и снова может быть выбранной. Таким образом, вероятность попадания каждой отдельной единицы в выборку равна 1/N и она остается постоянной на всем протяжении отбора.

Отбор по схеме «невозвращенного шара» называется бесповторной выборкой. В этом случае отобранная единица не возвращается в генеральную совокупность, и тем самым вероятность попадания еденицы в выборку изменяется от 1/N для 1-ой отобранной ед. до 1/N-n+1/

В социально-экономических исследованиях, как правило, не применяют повторный отбор.

27. Ошибки выборочного наблюдения.

Ошибка выборки или ошибка репрезентативности – это разница между знач-ем показателя выборочной и генеральной совокупности.

Расчет ошибок позволяет решить одну из главных про­блем орг-ции выборочного наблюдения — оценить реп­резентативность (представительность) выборочной сов-­сти. Различают среднюю и предельную ошибки выборки. Эти 2 вида связаны след соотношением:

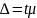
Где Δ-предельная ошибка выборки;t-коэф-т доверия. определяемый в завсим-ти от ур-ня вероятности;μ-средняя ошибка выборки

Величина средней ошибки выборки рассчитывается дифференцированно в завис-ти от способа отбора и процеду­ры выборки. Так, при случайном и механическом повторном отборе средняя ошибка выборки для средней величины (μ_x) опред-ся по формуле:

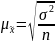
При бесповторном:

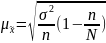
где σ²— генеральная дисперсия признака; n- объем выборочной совокупности; N — объем гене­ральной сов-сти; - выборочная средняя величина.

На практике величина дисперсии признака в генеральной совокупности (Ϭ² ), как правило, неизвестна, поэтому ее заменяют выборочной дисперсией ( S² ).

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в кот будут нах-ся хар-ки генер сов-ти. Например, для выборочной средней такие пределы устан-ся на основе след соотношений:

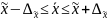
Где - генеральная средняя величина , Δ_х — предельная ошибка выборочной средней.

Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

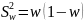
где w – доля единиц, обладающих данным значением признака в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки (m/n).

Тогда, например, при собственно-случайном и механическом отборах для определения средней ошибки выборки для доли признака используется следующая формула:

При повторном отборе:

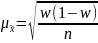
При бесповторном отборе:

числа серий r.