Вопрос 24. Правило сложения дисперсий и его использование в анализе взаимосвязи

Показатели вариации могут быть использованы не только в анализе изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями. Для сгруппированной, т. е. разделенной на i групп, статистической совокупности возможно вычисление трех видов дисперсий общей, внутригрупповых и межгрупповой. Общая дисперсия ( ) характеризует колеблемость признака признака во всей изучаемой сов-ти и рассчитывается по не сгруппированным данным по формуле

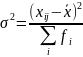
Где 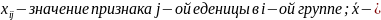среднее значение признака в совокупности; -число единиц в i-ой группе.

Для оценки колеблемости признака внутри каждой i-ой группе вычисляют внутригрупповые дисперсии (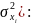

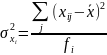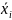, Где -среднее значение признака в i-ой группе. Обобщённую характеристику внутригрупповой колеблемости вокруг групповых средних дает средняя величина из внутригрупповых дисперсий:

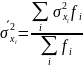
Межгрупповая дисперсия (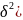 показывает вариацию групповых средних вокруг средней величины признака в совокупности:

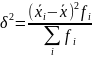
Между всеми указанными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий- общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:

σ² = σ¯_xi²+ δ² Логика этого правила такова: общая вариация признака в совокупности складывается из вариаций признака внутри отдельных групп и вариаций между группами. Правило сложения дисперсий широко применяется при исчислении показателей тесноты связей, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев.

На основании правила сложения дисперсий можно опре­делить показатель тесноты связи между факторным и результативным признаками. Он наз-ся эмпирическим корреляционным отношением и рассчитыва­ется по формуле:

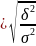
27/2

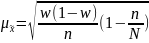
Пределы доли признака в генеральной совокупности (р) рассчитываются следующим образом: w − Δw ≤ ρ ≤ w + Δw.

Ошибки и пределы генеральных характеристик при других способах формирования выборочной совокупности определяются на основе соответствующих формул, отражающих особенности этих видов выборки. Например, в случае типической выборки показателем вариации является средняя из внутригрупповых дисперсий, при серийной выборке – межгрупповая (межсерийная) дисперсия и т.д. Кроме того, в последнем случае вместо объема выборочной совокупности n используется показатель

Вопрос 25.Понятие о выборочном наблюдении. Причины его применения и преимущества.

Выборочное наблюдение-это такой вид наблюдения, при котором обследованию подвергается не вся изучаемая совокупность, а лишь часть её единиц, отобранных в определенном порядке. При этом вся исследуемая совокупность наз-ся генеральной, а единицы подлежащие наблюдению, составляют выборочную совокупность или выборку.

Далее параметры выборочной совокупности (выборочная средняя величина, медиана, доля признака, среднее квадратическое отклонение) распространяются на генеральную совокупность. В этом

состоит сущность выборочного наблюдения и его преимущество перед другими видами несплошного наблюдения.

Разница между генеральными и выборочными параметрами называется ошибкой выборки или ошибкой репрезентативности. Формулы ее определения, разработанные теорией вероятностей и математической статистикой, дифференцированы в зависимости от видов и способов отбора.

Средние и относ-ые величины, полученные по отобранной части единиц, достаточно точно воспроизводят соотв-щие показатели сов-сти в целом. Эта особенность выборочного метода позволяет исп-ть его с целью экономии затрат времени и труда. Кроме того, выборочное наблюд. дает возможность значительно расширить программу стат-го наблюд. и делать его более детальным, т.к. исследованию подвергаются сравнительно небольшая часть совок-ти. Выборочное наблюд. находит широкое применение во всех отраслях хоз. деят-ти, в том числе и торговле (выявляется покупательский спрос, проверяются нормы естественной убыли товаров и др.). В выводной статистике принято строго различать параметры генеральной совокупности и их оценке по данной выборке. С этой целью принята следующая система обозначений (Генеральная: ср. велич. – , относ. велич. – р, дисперсия – Ϭ, коэффициент корреляции-δ²; объем сов-ти – N. Выборочная: ср. велич. –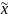 , относ. велич. – w, дисперсия – S², коэффициент корреляции-z²; объем сов-ти – n).