20. Структурные средние (мода и медиана).
Для целей аналитической и сравнительной характеристики различных рядов распределения принимается система обобщающих пок-лей вариационного ряда. Мода и медиана относятся к показателям центра распределения.
Мода – величина признака чаще всего встречающегося в исследуемой со-сти. В дискретном вариационном ряду модой явл-ся значение признака с наибольшей частотой.
В
интервальном ряду мода рассчит-ся по
ф-ле:
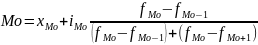где: x0
- нижняя граница интервала содержащего
моду; iM0-вел-на
мод инт-ла; fMo-
частота в мод интервале; fMo-1
- частота в инт-ле, предшествующем
мод-му; fMo
+1-
частота в инт-ле, последующем за
мод-ным;Медиана
– значение признака, приходящееся на
середину ранжированной (упорядоченной)
совокупности, делящее ее на две равные
части.Вычисление медианы в дискретных
рядах распределения имеет специфику.
Если такой ряд распределения имеет
нечетное число членов, то медианой
будет вариант, находящийся в середине
ранжированного ряда. Если ранжированный
ряд распределения состоит из четного
числа членов, то медианой будет средняя
арифметическая из двух значений
признака, расположенных в середине
ряда. Медиана интервального ряда
распределения определяется по формуле:
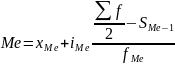где xMе – нижняя граница значения
интервала, содержащего медиану; iМе–
величина медианного интервала; – сумма
частот; SМе-1 – сумма накопленных частот,
предшествующих медианному интервалу;
fМе – частота медианного интервала.
Медианным явл-ся инт-л, в кот накопленная частота превышает половину численности сов-ти.
Накопленная частота – частота, полученная сложением частоты данного интервала и частот во всех предыдущих интервалах.
21. Общее понятие о вариации признака. Построение вариационных рядов и их графическое изображение.
Вариация – различие индивид-х значений признака у отд-х ед-ц сов-сти в один и тот же период или момент времени.
Первым этапом стат-кого изучения вариации явл-ся построение вариац-ного ряда, т е упоряд-ного распред-я ед-ц сов-сти по возраст-щим или убывающим значениям признака и подсчёт числа ед-ц с тем или иным значением.
Вариац ряды строятся по колич-му признаку (признак можно выразить итоговым значением). Сущ-ют также ряды распр-я, построенные по атрибутивным признакам (признаки не поддающиеся числовому выражению).Сущ-ют три формы вариационного ряда: Ранжированный ряд – перечень отд-х ед-ц сов-сти в порядке возрастания или убывания значений изучаемого признака. Например, список предприятий, расположенных в порядке возрастания уровня рентабельности каждого предприятия.2. Дискретный вариац ряд представляет собой таблицу, состоящую из двух граф или строк: конкретных значений признака и числа ед-ц сов-сти с тем или иным значением. Пример, распределение студентов группы по результатам экзамена.
3. Интервальный вариац ряд представляет собой таблицу, сост из двух граф или строк: интервалов значения признака и числа ед-ц сов-сти, попадающих в данный интервал (частот). Пример, распределение сотрудников фирмы по уровню заработной платы.На графике дискретный вариационный ряд изображается в виде полигона распределения, а интервальный – в виде гистограммы (столбиковой диаграммы).