39. Понятие статистической оценки. Свойства оценок: несмещенность, состоятельность, эффективность.

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные. ля того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть   есть статистическая оценка неизвестного параметра   теоретического распределения. Допустим, что по выборке объема   найдена оценка  . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку   и т. д. Получим числа  , которые будут различаться. Таким образом, оценку   можно рассматривать как случайную величину, а числа   — как возможные ее значения. Если оценка   дает приближенное значение   с избытком, то найденное по данным выборок число   будет больше истинного значения  . Следовательно, и математическое ожидание (среднее значение) случайной величины   будет превышать  , то есть  . Если   дает приближенное значение   с недостатком, то  .

Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки   было равно оцениваемому параметру. Соблюдение требования  устраняет систематические ошибки.

Несмещенной называют статистическую оценку  , математическое ожидание которой равно оцениваемому параметру  , то есть  .

Смещенной называют статистическую оценку  , математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки  ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при   стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при   стремится к нулю, то такая оценка оказывается также состоятельной.

40. Метод максимального правдоподобия и точечное оценивание характеристик распределения (эмпирическая частота, выборочное среднее, выборочная дисперсия, Интервальное оценивание.

Ме́тод максима́льного правдоподо́бия в математической статистике - это метод оценивания неизвестного параметра путём максимизации функции правдоподобия. Метод максимального правдоподобия -- это матстатистический метод поиска параметров некоторой модели, которой, предположительно удовлетворяет распределение и вообще характер поведения случайной величины. Например, мы знаем, что автобус ходит сравнительно регулярно (через примерно равные интервалы). Тогда, мы можем построить модель событий его появления на остановке, просто расставив точки на прямой в координатах (время; № появления на остановке). При этом, имея несколько зарегистрированных фактов появления автобуса на остановке, мы должны подобрать наклон и высоту прямой так, чтобы она проходила максимально близко к нарисованным нами в соответствии с имеющимися данными точкам. Обычно мы это делаем методом наименьших квадратов, и та невязка, которую мы минимизируем с помощью МНК, и является функцией правдоподобия (точнее, обратной к ней). Найдя наклон и высоту, мы заявляем: вот это -- наиболее правдоподобные параметры модели движения автобуса. Метод максимума правдоподобия (термин был впервые использован в работе Фишера, 1922) - это общий метод оценивания параметров генеральной совокупности с помощью максимизации функции правдоподобия (L) выборки. Функция правдоподобия L выборки из n наблюдений x₁, x₂, ..., x_n в случае дискретного распределения переменных  x₁, x₂, ..., x_n описывается функцией совместного распределения p(x₁, x₂, ..., x_n). Если x₁, x₂, ..., x_n имеют непрерывное распределение, функция правдоподобия L выборки из n наблюдений x₁, x₂, ..., x_n описывается совместной плотностью распределения f(x₁, x₂, ..., x_n). Пусть L - функция правдоподобия выборки; при наблюдаемых значениях x₁, x₂, ..., x_n L является функцией параметров  ₁,  ₂, ...  _k. Тогда оценками максимального правдоподобия  ₁,  ₂, ...  _k называются значения параметров   ₁,  ₂, ...  _k, максимизирующие функцию L. Очевидно, оценки зависят от наблюдений x₁, x₂, ..., x_n. В широких предположениях эти оценки являются оптимальными.

Пусть   - это элемент пространства  . Если   - открытый интервал, а L( ) дифференцируема и достигает максимума на  , то оценки МП удовлетворяют уравнению (dL( ))/d  = 0.

Ч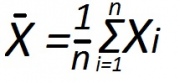 исла, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами. Эмпирическая частота, частота поостренная на наблюдениях. Выборочной средней называется среднее арифметическое значений признака выборочной совокупности.

Выборочная дисперсия- это оценка теоретической дисперсии распределения на основе выборки. Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения, характеризует разброс выборочных значений. Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.