
- •Количество информации. Единицы измерения количества информации. Вероятностный и количественный подход к определению количества информации.
- •Системы счисления. Основные характеристики позиционных систем счисления. Перевод чисел в позиционных системах счисления. Арифметические операции в позиционных системах счисления.
- •Основы логики. Базовые логические операции. Таблицы истинности.
- •Программное обеспечение пк. Классификация программного обеспечения.
- •Операционная система и ее задачи. Классификация ос. Современные ос.
- •Организация хранения данных. Файловая система, ее задачи. Основные понятия файловой системы. Ярлыки.
- •Ос ms Windows. Объекты ms Windows. Виды меню, главное меню. Окна. Стандартные операции с объектами ms Windows. Перенос и копирование объектов. Буфер обмена.
- •Навигация в ms Windows. Способы навигации и их сравнительная характеристика. Поиск файлов и папок средствами ms Windows. Параметры задаваемые для поиска.
- •Системы подготовки текстов. Текстовые процессоры. Текстовый процессор ms Word. Функциональные возможности. Настойка окна ms Word. Стандартные операции с документами.
- •Основные структурные единицы документа. Ввод и редактирование текста. Форматирование средствами ms Word.
- •Работа с таблицами средствами ms Word. Создание и форматирование таблицы.
- •Работа с рисунками ms Word. Создание рисунков, операции с рисунками, вывод формул.
- •Параметры страницы документа ms Word. Разрыв страницы. Раздел документа. Номера страниц, колонтитулы. Сноски, проверка правописания. Оглавление.
- •Электронные таблицы назначение. Табличный процессор ms Excel. Функциональные возможности. Стандартные операции с документами.
- •Понятие книга и лист в табличном процессоре Excel. Стандартные операции с листами. Ячейка таблицы, адреса ячеек. Формат данных в ячейках. Оформление таблицы.
- •Расчетные операции средствами ms Excel. Ввод и редактирование формул. Стандартные встроенные функции. Копирование и перенос формул. Фильтрация данных.
- •Построение диаграмм средствами ms Excel. Оформление и редактирование диаграммы.
- •Технологии обработки графической информации. Графические редакторы. Растровая и векторная графика, сравнительная характеристика. Цветовые модели.
- •Электронные презентации. Программа ms Point. Функциональные возможности. Создание презентации. Режим отображения слайдов, режим сортировщик слайдов.
- •Базы данных. Системы управления базы данных. Классификация баз данных.
- •Реляционная база данных. Структура базы данных. Таблица. Поле. Запись. Ключевое поле. Связь между таблицами, типы связей.
- •Программа ms Access. Объекты, таблица, форма, запрос. Виды запроса. Фильтрация данных, виды фильтров.
- •Этапы подготовки задач к решению на компе.
- •Системы программирования. Языки программирования, классификация. Трансляторы, компиляторы и интерпретаторы.
- •Понятие алгоритма. Основные свойства алгоритмов. Базовые алгоритмические конструкции. Понятие о структурно и объектно- ориентированном программировании.
- •Компьютерные сети, классификация. Принципы организации и основные топологии.
- •Адресация в сети. Протоколы.
- •Информационная безопасность. Методы защиты информации в сетях.
- •Услуги сети интернет. Понятие e-mail. Поиск информации.
- •Архивация и разархивация файлов. Программы архивации. Архивный файл. Самораспаковывающиеся пакеты.
- •Компьютерные вирусы. Классификация. Основные пути проникновения и признаки появления вирусов. Антивирусные программные средства.
- •Случайные величины и функции распределения вероятностей, дискретные случайные величины.
- •Непрерывные случайные величины и функция плотности вероятности.
- •Характеристики распределения случайной величины (математическое ожидание, дисперсия, медиана и мода). Примеры распределения случайных величин.
- •40.Непрерывное и дискретное равномерное распределение. Нормальное распределение.
- •42. Понятие случайной выборки. Примеры реальных биологических экспериментов.
- •43 Дескриптивные и графические методы анализа данных. Гистограмма: эмпирическая функция распределения. .
- •Столбчатые и секторные диаграммы.
- •Понятие статистической оценки. Свойства оценок: несмещенность, состоятельность, эффективность.
- •Метод максимального правдоподобия и точечное оценивание характеристик распределения (эмпирическая частота, выборочное среднее, выборочная дисперсия, Интервальное оценивание.
- •Доверительный интервал. Доверительные интервалы для математического ожидания и дисперсия нормального распределения.
- •Логика проверки статистических гипотез. Ошибки первого и второго рода, уровень значимости и мощность критерия.
- •Одновыборочные и двухвыборочные критерии. Сравнение параметров биноминальных и пуассоновских распределений.
- •Линейный регрессионный анализ. Множественная линейная регрессия.
- •Доверительные интервалы и проверка гипотез в линейном регрессионном анализе.
- •Корреляционный и дисперсионный анализ
40.Непрерывное и дискретное равномерное распределение. Нормальное распределение.
Д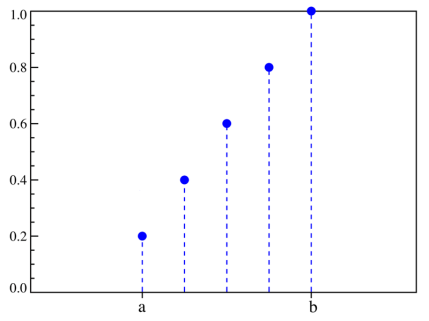
 искретное
равномерное
распределение,
если она принимает конечное число
значений с равными вероятностями.
Случайная
величина, принимающая значение 1,
если выпал орёл, и 0, если выпала решка,
имеет дискретное равномерное распределение.
Она принимает оба значения с вероятностью
1/2. Рисунок дискретного равномерного
распределения. Случайная величина,
равная выпавшему числу на игральной
кости, имеет дискретное равномерное
распределение на {1,2,3,4,5,6}, и она
принимает каждое значение с вероятностью
1/6.
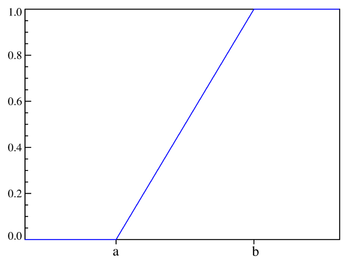
Непрерывная
случайная величина имеет равномерное
распределение
на отрезке a,b
, если на этом отрезке плотность
распределения случайной величины
постоянна, а вне его равна нулю, т.е
вероятность любого интервала зависит
от его длины. Рисунок функции непрерывного
равномерного распределения. Формула
непрерывного равномерного распределения.
искретное
равномерное
распределение,
если она принимает конечное число
значений с равными вероятностями.
Случайная
величина, принимающая значение 1,
если выпал орёл, и 0, если выпала решка,
имеет дискретное равномерное распределение.
Она принимает оба значения с вероятностью
1/2. Рисунок дискретного равномерного
распределения. Случайная величина,
равная выпавшему числу на игральной
кости, имеет дискретное равномерное
распределение на {1,2,3,4,5,6}, и она
принимает каждое значение с вероятностью
1/6.
Непрерывная
случайная величина имеет равномерное
распределение
на отрезке a,b
, если на этом отрезке плотность
распределения случайной величины
постоянна, а вне его равна нулю, т.е
вероятность любого интервала зависит
от его длины. Рисунок функции непрерывного
равномерного распределения. Формула
непрерывного равномерного распределения.
Н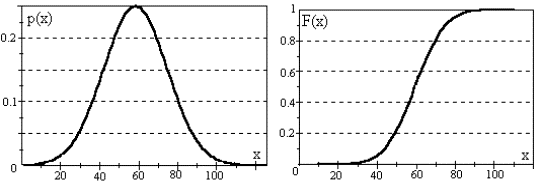 ормальное
распределение называется
нормальное распределение с математическим
ожиданием 0 и стандартным отклонением
1.
Формула
плотности нормального распределения
ормальное
распределение называется
нормальное распределение с математическим
ожиданием 0 и стандартным отклонением
1.
Формула
плотности нормального распределения
![]() Формула функции нормального распределения
Формула функции нормального распределения
 Пример, рост живых организмов, погрешности
в стрельбе. Рисунок плотности нормального
распределения и рисунок функции
нормального распределения.
Пример, рост живых организмов, погрешности
в стрельбе. Рисунок плотности нормального
распределения и рисунок функции
нормального распределения.
Правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит уравненного среднего квадратического отклонения. Выборочные характеристики это средние показатели, применимые для следующих целей: количественно охарактеризовать самые существенные свойства распределения, для сравнения различных распределений. Виды выборочных характеристик: средние величины, выборочные и центральные моменты (ассимитрия и акцесс), показатели вариации.
42. Понятие случайной выборки. Примеры реальных биологических экспериментов.
Выборка это процедура отбора подмножества наблюдений из всех возможных, для того чтобы получить заключение обо всем множестве наблюдений. Случайная выборка это выборка для которой каждый элемент генеральной совокупности имеет определенную заранее заданную вероятность быть отобранным. Такая выборка является наиболее точной. По определению в случайной выборке выполняется принцип случайности. У всех элементов генеральной совокупность есть шанс быть выбранными. Для обеспечения шансов этой выборки социолог формирует основу, т.е полный список всех элементов генеральной совокупности. Например, основой выборки могут быть списки работников предприятия, телефонный справочник, количество кошек пришедших в клинику. Плюсом данного метода является полное соблюдение принципа случайности, и как следствие избежание систематических ошибок. Простая случайная выборка. Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел. Примером такой выборки может служить дозвон на случайный номер. Систематическая выборка. Первый элемент в такой выборке указывается случайно, и затем последовательно отбирается каждый k-ый элемент. Здесь примером могут быть квартирные выборки, когда интервьюер посещает квартиры по определенной схеме. Стратифицированная выборка. Генеральная совокупность разбивается на группы (страты) по какому-либо признаку, например, полу, возрасту или географическому положению. Затем, в каждой страте отбор осуществляется случайным или механическим образом. Кластерная выборка. При такой выборке единицами отбора выступают не сами объекты, а группы (кластеры). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком. В некоторых классических экспериментах с селекцией гороха Мендель наблюдал частоты различных видов семян, получаемых при скрещивании растений с круглыми желтыми семенами и растений с морщинистыми зелеными семенами. Они приводятся ниже вместе с теоретическими вероятностями, вычисленными в соответствии с теорией наследственности Менделя.
