10.Наведіть формулу для обчислення енергії сигналу, який має обмежений спектр, та поясніть, чому ця формула приблизна.

Для перетворення потоку імпульсних відліків у неперервну функцію їх пропускають через ідеальний фільтр нижніх частот з граничною частотою F.

Енергія сигналу знаходять за формулою

(4.16)

Для сигналу, обмеженого у часі формула (4.16) перетворюється до виду

(4.17)

Формула (4.17) є приблизною, бо сигнали не можуть бути одночасно обмежені за частотою й за часом. У макросвіті місце принцип невизначеності аналогічний принципу невизначеності Гейзенберга у квантовій механіці.

11.Поясніть, які висновки слідують із теореми Котельникова.

У теоремі Котельникова розглядається ідеальний випадок, коли сигнал почався нескінченно давно і ніколи не закінчиться, а також не має у своїй часовій характеристиці точок розриву. Реальні сигнали не мають таких характеристик. Вони конечні за часом і за звичай мають розриви у часовій характеристиці. Відповідно, їх спектр нескінченний. Тоді повне відновлення сигналу не можливе. Із теореми Котельникова витікають два висновки:

-  будь-який аналоговий сигнал може бути відновлений з якою завгодно точністю за своїми дискретними відліками, взятими з частотою f > 2f_c, де f_c – максимальна частота, якою обмежено спектр реального сигналу;

- якщо максимальна частота у сигналі перевищує половину частоти дискретизації, то не існує способу відновлення сигналу із дискретного в аналоговий без спотворень.

12.Сформулюйте теорему відліків для частотної області.

Теорему відліків можна сформулювати і для частотної області, що буде дуальною теоремою до теореми відліків у часовій області.

Така теорема стверджує: якщо аналоговий сигнал s(t) має обмежену тривалість, то його спектр може бути однозначно відновлено за своїми вибірками, що взяті з інтервалом:

, (4.18)

де Δf – інтервал частотних вибірок сигналу; T₀ – період сигналу.

Загальний висновок. Для правильної цифрової обробки сигналів частота дискретизації повинна бути досить високою і сигнали мають бути ретельно відфільтровані перед їх оцифровуванням.

13.Покажіть спектральне представлення гармоніки: гармонічна частота на шкалі частот та на шкалі фази.

Сигнали можна представляти функціями часу або у вигляді частотних спектрів. При дослідженні ПЕМВН сигнали зазвичай представляються у вигляді частотних спектрів.

Якщо сигнал визначається гармонічною функцією Acos(ωt +ψ), то на шкалі частот вона визначається заданою амплітудою А та початковою фазою ψ (рис. 4.4).

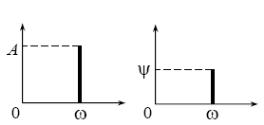
Рисунок 4.4 – Звичне спектральне представлення гармоніки: гармонічна частота на шкалі частот та на шкалі фази

14.Запишіть формулу комплексного представлення косинусоїди та покажіть представлення гармоніки для комплексної форми запису косинусоїди.

За комплексної форми запису косинусоїди

. (4.19)

вводиться чисто математичне поняття негативної кутової частоти, а шкала частот доповнюється негативною на піввіссю. Амплітудний і фазовий спектр в цьому випадку зображаються парами ординат (рис. 4.5), відповідних позитивні і негативним значенням кутової частоти.

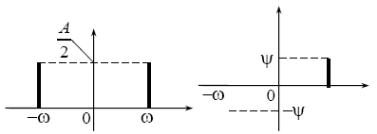
Рисунок 4.5 – Спектральне представлення гармоніки для комплексної форми запису косинусоїди

14. Наведіть тригонометричну форму запису ряду Фур’є для функції f(t), та формули для амплітуди та коефіцієнтів розкладення. Наведіть комплексну форму запису ряду Фур’є для функції f(t), та формули для комплексної амплітуди та коефіцієнтів розкладення.

Не синусоїдальні сигнали можуть бути розкладені в ряд Фур’є, тобто представлені у вигляді дискретного ряду гармонік.

Для тригонометричної форми запису ряду Фур’є для функції

(4.20)

амплітуди A_n і початкові фази ψ_n визначаються формулами

; , (4.21)

де n – номер гармоніки.

В (4.21) коефіцієнти розкладення

; , (4.22)

де Т – період основної частоти, ω₁ = 2πT – основна частота.

Для комплексної форми запису ряду Фур’є

(4.23)

комплексні амплітуди визначаються за формулою

. (4.24)

у якій A_n, ψ_n, a_n, b_n обчислюються за раніше наведеними формулами.

Сукупність амплітуд відповідних гармонік (модулів комплексних коефіцієнтів ряду Фур’є, відкладених проти відповідних позитивних і негативних частот) представляє симетричний щодо осі ординат лінійчатий амплітудний спектр.

Лінійчатий фазовий спектр утворюють аргументи (фази) комплексних коефіцієнтів ряду Фур’є.