1.Запишіть формулу прямого та оберненого перетворення Фур’є. Який фізичний смисл має перетворення Фур’є?

Перетворення Фур’є – це операція, яка описує коефіцієнти (так звані «амплітуди») при розкладенні початкової функції на елементарні складові – гармонічні коливання з різними частотами.

Перетворення Фур’є функції f дійсної змінної являється інтегральним та задається наступною формулою:

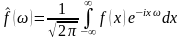. (4.1)

Формула обернення:

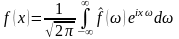(4.3)

є справедливою, якщо інтеграл у правій частині має смисл.

Ця формула пояснює фізичний смисл перетворення Фур’є: права частина – це нескінченна сума комплексних гармонічних коливань 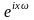з частотами ω, амплітудами 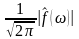та фазовими зсувами 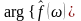, відповідно. Функція що описує коливання являється комплексною функцією.

2.Наведіть рівність Парсеваля та поясніть її фізичний смисл.

Справедливою є рівність Парсеваля: при певних широких умовах перетворення Фур’є зберігає так звану L₂ норму:

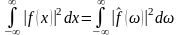(4.2)

З фізичного смислу це означає, що енергія зберігається. L₂ норму можна трактувати як закон зберігання енергії.

3.Запишіть формули перетворення Фур’є як перетворення функції часу у функцію частоти та розкладання часової функції на гармонічні складові з різними частотами.

Формули перетворення Фур’є у термінах часу та частоти. У області обробки сигналів перетворення Фур’є бере представлення функції сигналу у вигляді часових рядів (якщо замінити x на t) і відображає його у частотний спектр, де ω, – кутова частота.

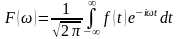. (4.4)

Тобто воно перетворює функцію часу у функцію частоти. А обернена формула є розкладанням часової функції на гармонічні складові з різними частотами. Іншими словами, перетворення Фур’є це декомпозиція сигналу на частоти та амплітуди, тобто є оборотним переходом від часового простору до частотного простору.

Коли функція f являється функцією часу та представляє фізичний сигнал, перетворення має стандартну інтерпретацію як спектр сигналу. Абсолютна величина, яка утворюється в результаті перетворення комплексної функції F представляє амплітуди відповідних частот (ω), а фазові зсуви отримують як аргумент цієї комплексної функції.

4.Як виглядає віконне перетворення Фур’є та поясніть його застосування у сучасних цифрових осцилографах і аналізаторах спектру.

Віконне перетворення. Класичне перетворення Фур’є має справу із спектром сигналу, взятим у всьому діапазоні існування змінної. Коли інтерес представляє тільки локальний розподіл частот, який концентрується у певному проміжку, то застосовують так зване віконне перетворення Фур’є. Спершу обирають деяку віконну функцію W. Тоді віконне перетворення виглядає як:

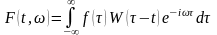,. (4.5)

де F(t, ω) дає дещо спотворений розподіл частот частини оригінального сигналу f(t) в околиці часу t.

Спектральний аналіз реалізовано в сучасних цифрових осцилографах і аналізаторах спектру. Використовується, як правило, вибір вікна з декількох (від 3 до 10) типів вікон. Застосування вікон принципово необхідне, оскільки в реальних приладах досліджується завжди деякий часовий відрізок з досліджуваного сигналу. При цьому розриви сигналу унаслідок вирізки різко спотворюють спектр через накладення спектрів стрибків на спектр сигналу. Знаходження оптимального виду вікна для віконного перетворення продовжує залишатись науковою проблемою.

Деякі аналізатори спектру використовують швидке (або короткочасне) віконне перетворення. При ньому сигнал заданої тривалості розбивається на ряд інтервалів за допомогою ковзаючого вікна того або іншого типу. Це дозволяє отримувати, досліджувати і будувати у вигляді спектрограм динамічні спектри й аналізувати їх поведінку в часі. Спектрограма будується в трьох координатах - частота, час і амплітуда. Подібні аналізатори спектру називають аналізаторами спектру реального часу. Основним їх виробником є корпорація Tektronix (США). Частотний діапазон досліджуваних ними сигналів досягає сотень гігагерц. Розроблено та експлуатуються вітчизняні аналоги.