
- •Тематичний план роботи
- •Означений інтеграл
- •Означений інтеграл зі змінною границею
- •Невластиві інтеграли, їх збіжність.
- •Диференціальні рівняння
- •Знакозмінні числові ряди
- •Степеневі ряди
- •Ряди Тейлора-Маклорена
- •Поняття про ряди Фур’є
- •Варіанти завдань для самостійного розв’язку
- •Контрольні питання теоретичного та практичного змісту в тестовій формі
- •Література
Диференціальні рівняння
Диференціальні рівняння (ДР) 1-го порядку. Класифікація ДР, їх алгоритми розв’язку.
ДР
1-го порядку, вирішеним відносно
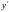 ,
називається рівняння вигляду
,
називається рівняння вигляду
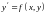 ,
тут
,
тут
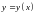 - невідома функція розв’язку даного
ДР. Розрізняють загальний розв’язок
даного ДР, який задається у вигляді
- невідома функція розв’язку даного
ДР. Розрізняють загальний розв’язок
даного ДР, який задається у вигляді
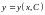 ,
,
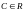 .
Якщо константа
.
Якщо константа
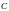 приймає одне із своїх можливих числових
значень, тоді загальний розв’язок
перетвориться в один із багатьох
частинних розв’язків вигляду
.
приймає одне із своїх можливих числових
значень, тоді загальний розв’язок
перетвориться в один із багатьох
частинних розв’язків вигляду
.
Задачею
Коші для ДР 1-го порядку називають саме
ДР, до якого додається одна початкова
умова вигляду
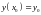 .
.
Теорема
Коші (в спрощеній формі). При деяких
обмеженнях на функцію
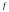 та її частинні похідні 1-го порядку,
розв’язок задачі Коші завжди існує
і він буде єдиним.
та її частинні похідні 1-го порядку,
розв’язок задачі Коші завжди існує
і він буде єдиним.
Геометрично
теорема Коші інтерпретується існуванням
деякої єдиної інтегральної кривої як
розв’язку початкового ДР, яка обов’язково
пройде через точку з координатами
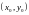 .
.
Розрізняють такі основні типи ДР 1-го порядку, які підлягають інтегруванню:
1)
ДР з відокремлюваними змінними. Це таке
ДР, для якого завжди
 ,
тоді, оскільки
,
тоді, оскільки
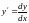 ,
,
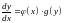 .
В останньому рівнянні виконаємо процедуру
відокремлення змінних: при
.
В останньому рівнянні виконаємо процедуру
відокремлення змінних: при
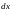 необхідно записати функцію, залежну
від змінної
необхідно записати функцію, залежну
від змінної ,
а при
,
а при
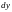 -функцію, залежну від
-функцію, залежну від
 :
: Тоді
Тоді
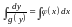 ,
або
,
або
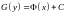 - загальний інтеграл початкового ДР,
при цьому
- загальний інтеграл початкового ДР,
при цьому
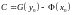 .
Зауваження: якщо функції-первісні
.
Зауваження: якщо функції-первісні
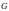 чи
чи
 записані натуральними логарифмами,
зручно замість
записувати
записані натуральними логарифмами,
зручно замість
записувати
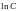 ,
і подальшим потенціюванням відповідь
спрощується.
,
і подальшим потенціюванням відповідь
спрощується.
2)
Однорідні ДР, їх характерною рисою є
така умова:
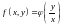 ,
тоді
,
тоді
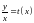 ,
або
,
або
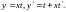 отже,
отже,
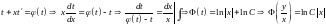 -
загальний інтеграл розв’язку.
-
загальний інтеграл розв’язку.
3) Лінійні неоднорідні ДР (ЛНДР) та рівняння Бернулі:
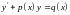 та
та
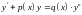 ,
,
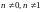 .
Якщо
.
Якщо
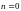 то рівняння
Бернулі
перетвориться в ЛНДР, якщо
то рівняння
Бернулі
перетвориться в ЛНДР, якщо
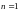 ,
то рівняння Бернулі стане ДР з
відокремленими змінними. Дані рівняння
рішаються аналогічно, наведемо алгоритм
їх розв’язку
на прикладі ЛНДР. Невідомий розв’язок
будемо шукати у вигляді добутку двох
невідомих функцій, тобто
,
то рівняння Бернулі стане ДР з
відокремленими змінними. Дані рівняння
рішаються аналогічно, наведемо алгоритм
їх розв’язку
на прикладі ЛНДР. Невідомий розв’язок
будемо шукати у вигляді добутку двох
невідомих функцій, тобто
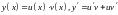 .
Тоді
.
Тоді
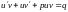 ,
або
,
або
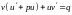 .
Підберемо функцію
.
Підберемо функцію
 так, щоб
так, щоб
 ,
тоді
,
тоді
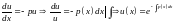 (для
береться частинний розв’язок, тобто
константа
відсутня). Для іншої функції
(для
береться частинний розв’язок, тобто
константа
відсутня). Для іншої функції
 маємо рівняння, що залишилось:
маємо рівняння, що залишилось:
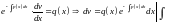 .
.
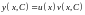 .
.
Приклади:
1.Знайти функціональну залежність для опису розпаду деякого
радіоактивного
матеріалу в залежності від часу
 ,
якщо відомо, що
,
якщо відомо, що
швидкість розпаду пропорційна масі матеріалу в даний момент часу, а
початкова
маса матеріалу -
 .
.
Нехай
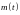 - маса радіоактивного матеріалу в момент
часу
.
Тоді
- маса радіоактивного матеріалу в момент
часу
.
Тоді
швидкість розпаду цього матеріалу визначається першою похідною
функції
 .
Тоді в силу умови
.
Тоді в силу умови
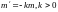 -
коефіцієнт пропорційності,
-
коефіцієнт пропорційності,
що характеризує властивості конкретного матеріалу. Знак «-» вказує, що
маса
матеріалу з бігом часу зменшується
 .
Тоді
.
Тоді
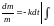
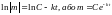 -
загальний розв’язок складеного рівняння
з
-
загальний розв’язок складеного рівняння
з
відокремлюваними
змінними. Знайдемо
:
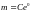 ,
звідки
,
звідки
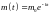 .
.
Якщо
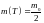 ,
тоді
,
тоді
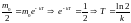 - величина часу,що
- величина часу,що
визначає період піврозпаду даного радіоактивного матеріалу.
2.На
тіло маси
,
що рухається вертикально вниз, діє сила
ваги цього тіла. Також на тіло діє сила
опору повітря, пропорційна швидкості
тіла в даний момент часу, з коефіцієнтом
пропорційності
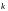 . Знайти залежність швидкості тіла від
часу.
. Знайти залежність швидкості тіла від
часу.
Згідно
2-го закону Ньютона
 ,
або
,
або
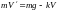 або
або
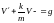 - це ЛНДР. Нехай
- це ЛНДР. Нехай
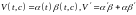 ,
,
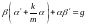 ,
, ,
тоді для іншої функції
,
тоді для іншої функції
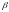 маємо таке рівняння:
маємо таке рівняння:
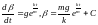 .
.
Тоді
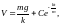
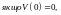 то
то
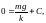 і остаточно
і остаточно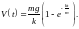
3.
Знайти рівняння кривої, для якої відрізок,
що відтинається дотичною на осі абсцис,
дорівнює квадрату ординати точки дотику.
В силу умови задачі з використанням
геометричного змісту похідної стосовно
невідомої функції
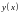 маємо диференціальне рівняння вигляду:
маємо диференціальне рівняння вигляду:
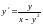 .
Це рівняння у даному вигляді жодному з
випадків інтегрування не підлягає.
Але оскільки
.
Це рівняння у даному вигляді жодному з
випадків інтегрування не підлягає.
Але оскільки
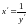 ,
то рівняння може бути переписане у
вигляді
,
то рівняння може бути переписане у
вигляді
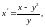 де
де
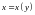 ,
або
,
або
 з невідомою функцією
з невідомою функцією
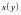 ,
для якої
,
для якої
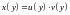 ,
тобто останнє рівняння розв’язуємо як
ЛНДР з невідомою функцією
.
Маємо
,
тобто останнє рівняння розв’язуємо як
ЛНДР з невідомою функцією
.
Маємо
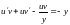 ,
,
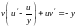 ,
,
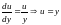 ,
,
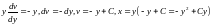 -
загальний розв’язок
сімейства кривих (очевидно, це сімейство
парабол), що задовольняють умові задачі.
-
загальний розв’язок
сімейства кривих (очевидно, це сімейство
парабол), що задовольняють умові задачі.
Лінійні неоднорідні ДР 2-го порядку з постійними коефіцієнтами.
Даний
тип диференціальних рівнянь визначається
у вигляді
 ,
тут
,
тут
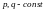 ,
якщо
,
якщо
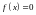 ,
то рівняння перетворюється у відповідне
однорідне. Задачею
Коші
для даного рівняння називається саме
ДР і дві початкові умови вигляду
,
то рівняння перетворюється у відповідне
однорідне. Задачею
Коші
для даного рівняння називається саме
ДР і дві початкові умови вигляду
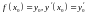 .
Має місце аналогічна теорема Коші про
існування та єдність розв’язку задачі
Коші. Нехай
.
Має місце аналогічна теорема Коші про
існування та єдність розв’язку задачі
Коші. Нехай
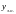 - загальний розв’язок
однорідного ДР,
- загальний розв’язок
однорідного ДР,
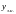 - загальний розв’язок
неоднорідного ДР, для якого справедлива
теорема:
- загальний розв’язок
неоднорідного ДР, для якого справедлива
теорема:
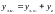 ,
де
,
де
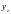 -
довільний частинний розв’язок
неоднорідного ДР. Для знаходження
по однорідному ДР складемо відповідне
характеристичне
рівняння
виду:
-
довільний частинний розв’язок
неоднорідного ДР. Для знаходження
по однорідному ДР складемо відповідне
характеристичне
рівняння
виду:
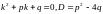 -
його дискримінант. Можливі випадки:
-
його дискримінант. Можливі випадки:
а)
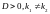 - дійсні та різні корені характеристичного
рівняння, тоді
- дійсні та різні корені характеристичного
рівняння, тоді
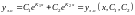 .
.
б)
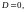
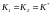 -
дійсні однакові корені характеристичного
рівняння
-
дійсні однакові корені характеристичного
рівняння
 ,
тоді
,
тоді
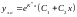 .
.
в)
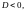 корені
характеристичного рівняння є комплексними
(комплесноспряженими) числами.
корені
характеристичного рівняння є комплексними
(комплесноспряженими) числами.
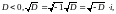
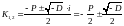 і нехай
і нехай
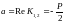 -
дійсна частина коренів характеристичного
рівняння
-
дійсна частина коренів характеристичного
рівняння
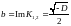 -
уявна частина коренів характеристичного
рівняння, тоді
-
уявна частина коренів характеристичного
рівняння, тоді
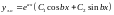 .
можливо знайти, якщо
- спеціальна права частина (квазімногочлен)
1-го типу:
.
можливо знайти, якщо
- спеціальна права частина (квазімногочлен)
1-го типу:
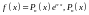 - многочлен степені
- многочлен степені
 .
Підберемо
.
Підберемо
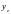 у вигляді:
у вигляді:
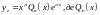 -
загальний вигляд многочлена степені
з неозначеними коефіцієнтами,
-
загальний вигляд многочлена степені
з неозначеними коефіцієнтами,
 - кількість співпадань числа
- кількість співпадань числа
 з коренями
з коренями
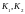 характеристичного рівняння. Квазімногочлен
2-го роду, це вираз вигляду:
характеристичного рівняння. Квазімногочлен
2-го роду, це вираз вигляду:
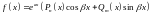 ,
тоді
,
тоді
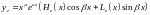 ,
,
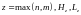 - різні многочлени степенів
- різні многочлени степенів
 з неозначеними коефіцієнтами,
- приймає значення 0 або 1, і дорівнює 1
тільки тоді, коли комплексне число
з неозначеними коефіцієнтами,
- приймає значення 0 або 1, і дорівнює 1
тільки тоді, коли комплексне число
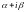 співпаде з одним із комплексних коренів
характеристичного рівняння.
співпаде з одним із комплексних коренів
характеристичного рівняння.
Приклади:
1)
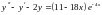 ,
,
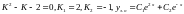 с
с
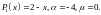
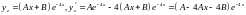 ,
,
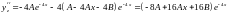 .
Значення
та його похідних підставимо в початкове
неоднорідне ДР:
.
Значення
та його похідних підставимо в початкове
неоднорідне ДР:
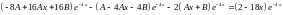
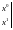
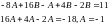
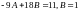 .
Отже
.
Отже
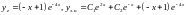 .
Нехай
.
Нехай
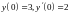 .
.
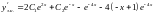 .
Тоді
.
Тоді
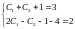 або
або
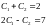
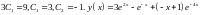 -
розв’язок задачі Коші.
-
розв’язок задачі Коші.
2)Розв’язати:

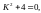
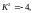
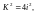
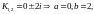
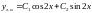
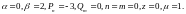 отже
отже
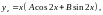
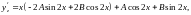
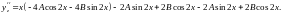 підставимо ці результати в початкове
рівняння
підставимо ці результати в початкове
рівняння
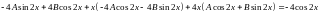 .
.
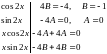
Таким
чином
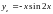 .
.
Зауваження.
Якщо в неоднорідності 2-го роду
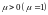 ,
тоді відповідне ДР відповідає випадку
резонансу,
тобто необмеженому збільшенню амплітуди
коливань деякої механічної системи зі
збільшенням аргументу.
,
тоді відповідне ДР відповідає випадку
резонансу,
тобто необмеженому збільшенню амплітуди
коливань деякої механічної системи зі
збільшенням аргументу.
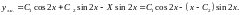 Із
вигляду отриманого розв’язку, якщо
Із
вигляду отриманого розв’язку, якщо
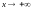 ,
видно, що визначальним у ньому є другий
доданок, і відповідною змінною амплітудою
синусоїди буде значення
,
видно, що визначальним у ньому є другий
доданок, і відповідною змінною амплітудою
синусоїди буде значення
 ,
якщо
,
що дійсно відповідає визначенню
резонансу.
,
якщо
,
що дійсно відповідає визначенню
резонансу.
Ряди
Числові ряди
Якщо
задана деяка числова послідовність
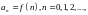 то
нескінченним числовим рядом називається
сума членів цієї числової послідовності,
тобто
то
нескінченним числовим рядом називається
сума членів цієї числової послідовності,
тобто
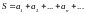 Головним питанням для таких рядів є
питання їх збіжності.
Числовий ряд називається збіжним, якщо
існує і є сталою нескінчена сума членів
цього ряду, і, відповідно, розбіжним,
якщо значення такої суми не існує.
Головним питанням для таких рядів є
питання їх збіжності.
Числовий ряд називається збіжним, якщо
існує і є сталою нескінчена сума членів
цього ряду, і, відповідно, розбіжним,
якщо значення такої суми не існує.
Теорема
1. (необхідна умова збіжності). Для
збіжності числового ряду необхідно,
щоб
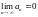 .
Якщо ця умова не виконується,то числовий
ряд завідомо розбіжний.
.
Якщо ця умова не виконується,то числовий
ряд завідомо розбіжний.
Приклад.
Встановити збіжність
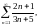 тут
тут
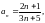
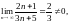 отже ряд розбіжний.
отже ряд розбіжний.
Теорема
2. Задано два числових ряди
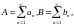 для яких
для яких
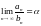 ,
,
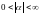 ,
тобто ці ряди еквівалентні на
нескінченності. Тоді такі два ряди
збіжні або розбіжні одночасно.
,
тобто ці ряди еквівалентні на
нескінченності. Тоді такі два ряди
збіжні або розбіжні одночасно.
Теорема
3. Задано числовий ряд
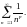 Такий ряд збіжний, якщо
і розбіжний, якщо
.
Такий ряд збіжний, якщо
і розбіжний, якщо
.
Приклад.
Дослідити збіжність ряду
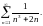 Такий ряд буде еквівалентним ряду
Такий ряд буде еквівалентним ряду
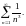 ,
для якого
,
і
в силу теорем 2 і 3 обидва ряди будуть
збіжними.
,
для якого
,
і
в силу теорем 2 і 3 обидва ряди будуть
збіжними.
Розглянемо достатні ознаки збіжності числових рядів.
Теорема 4. (Ознака Даламбера)
Задано
числовий ряд
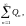 для якого
.
Тоді нехай
для якого
.
Тоді нехай
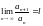 .
Якщо
.
Якщо
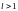 - ряд збіжний, якщо
- ряд збіжний, якщо
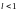 - ряд збіжний, якщо
- ряд збіжний, якщо
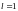 - дана ознака не дає відповіді на питання
про збіжність.
- дана ознака не дає відповіді на питання
про збіжність.
Приклад:
встановити збіжність ряду
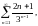 тут
тут
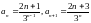 ,
,
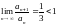 ,
отже ряд збіжний.
,
отже ряд збіжний.
Теорема 5. (Радикальна ознака Коші).
Якщо
для числового ряду
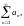
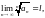 то при
ряд
розбіжний, при
- ряд збіжний, якщо
- дана ознака не працює.
то при
ряд
розбіжний, при
- ряд збіжний, якщо
- дана ознака не працює.
Приклад.
Встановити
збіжність
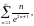
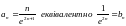 .
.
Для
ряду із
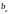 за теоремою 5 маємо:
за теоремою 5 маємо:
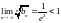 ,
отже ряд із
- збіжний, тоді в силу теореми 2 початковий
ряд теж збіжний.
,
отже ряд із
- збіжний, тоді в силу теореми 2 початковий
ряд теж збіжний.
Теорема 6. (інтегральна ознака Коші).
Задано
ряд
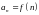 .
За функцією
запишемо відповідний невластивий
інтеграл вигляду
.
За функцією
запишемо відповідний невластивий
інтеграл вигляду
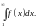 Тоді початковий числовий ряд та інтеграл
збіжні або розбіжні одночасно.
Тоді початковий числовий ряд та інтеграл
збіжні або розбіжні одночасно.
Приклад:
Встановити збіжність ряду
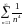 (тут
(тут
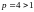 ).
Маємо
).
Маємо
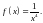 Тоді
Тоді
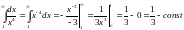 ,
отже невластивий інтеграл збіжний, і в
силу теореми 6 початковий ряд теж збіжний.
,
отже невластивий інтеграл збіжний, і в
силу теореми 6 початковий ряд теж збіжний.
