91

Міністерство аграрної політики та продовольства України

Вінницький національний аграрний університет

Кафедра вищої математики,інформатики

та математичних методів в економіці

МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ З ВИЩОЇ МАТЕМАТИКИ

Частина-II

НАВЧАЛЬНО-МЕТОДИЧНИЙ ПОСІБНИК

для студентів всіх спеціальностей ВНАУ

Вінниця-2013

УДК 517

Методичне забезпечення самостійної роботи студентів з вищої математики. Частина-II. Навчально-методичний посібник для студентів всіх спеціальностей /Дубчак В.М.- Вінниця: ВНАУ,2013.-124 c.

Дубчак В.М.,к.т.н.,доцент кафедри

вищої математики,інформатики та

математичних методів в економіці

Рецезенти: Михалевич В.М.,д.т.н.,професор,зав.кафедри

вищої математики ВНТУ,

Любін М.В.,к.т.н.,доцент кафедри ПОПХВ

ВНАУ

Посібник містить теоретичний матеріал, перелік типових стандартних практичних завдань з вищої математики, по кожному з яких пропонується 100 незалежних варіантів,з метою організації самостійної, домашньої, розрахунково-графічної роботи. Матеріали посібника можуть бути використані для організації роботи студентів всіх спеціальностей університету,які вивчають основи вищої математики.

Навчально-МЕТОДИЧНЕ ВИДАННЯ

Рекомендовано науково-методичною комісією

Вінницького національного аграрного університету

Протокол №___від «___»_____________ 2013 р.

ЗМІСТ

Зміст……………………………………………………………………………….3

Вступ …………………………………………………………………………... 4

Короткий теоретичний курс……………………………………………………. 6

Модуль 4

Означений інтеграл

1. Визначення та властивості означеного інтеграла ………………………… 6

2. Означений інтеграл зі змінною границею…………………………………..10

3. Методи обчислення означеного інтеграла………………………………….11

4. Геометричні додатки означених інтегралів………………………………..12

5. Невластиві інтеграли, їх збіжність………………………………………….14

Диференціальні рівняння

6. Визначення диференціальних рівнянь. Диференціальні

рівняння (ДР) 1-го порядку. Класифікація ДР, їх алгоритми розв’язку……15

7. Лінійні неоднорідні ДР 2-го порядку з постійними коефіцієнтами……...19

Модуль 5

Ряди

8. Ряди. Числові ряди………………………………………………………….21

9. Знакозмінні числові ряди…………………………………………………..23

10.Степеневі ряди………………………………………………………………24

11.Ряди Тейлора-Маклорена…………………………………………………..25

12.Поняття про ряди Фур’є……………………………………………………26

13.Варіанти завдань для самостійного розв’язку……………………………27

14. Контрольні питання теоретичного та практичного змісту в

тестовій формі…………………………………………………………………118

Література ……………………………………………………………………..123

ВСТУП

Навчальний посібник призначений для організації самостійної, домашньої, розрахунково-графічної роботи студентів всіх спеціальностей,що вивчають згідно своєї навчальної програми такі розділи вищої математики,такі як означені інтеграли,диференціальні рівняння та ряди. В роботі присутні короткі теоретичні матеріали по даним розділам вищої математики, в кожному із запропонованих завдань приведено по 100 незалежних варіантів для організації самостійної роботи як в межах аудиторної роботи так і за межами аудиторної,тобто самостійної. В кінці роботи запропоновано перелік рекомендованої літератури для виконання приведених самостійних завдань.

Тематичний план роботи

№ п/п	Мо- дуль	Назва теми	Види роботи	Види самостійної роботи,години	Форми контролю (іспит,залік, тести)
1	4	Озна- чений інтег- рал	Лекції, практичні заняття	Розрахунково-графічне завдання(РГЗ)-8 год.	Контрольна робота (КР),іспит
2	4	Дифе- ренці- альні рів- няння	Лекції, практичні заняття	Розрахунково-графічне завдання(РГЗ)-6 год.	Контрольна робота (КР), іспит
3	5	Ряди	Лекції, практичні заняття	Розрахунково-графічне завдання(РГЗ)-8 год.	Контрольна робота (КР),іспит

Означений інтеграл

Нехай задана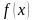 - неперервна на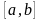 функція.

Розглянемо будь-який відрізок _,

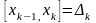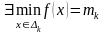, Отже 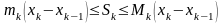Візьмемо в цій

подвійній нерівності

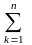
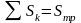(площа криволінійної трапеції)

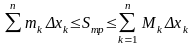
Виберемо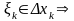 тоді

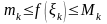
Оскільки 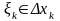- довільна точка, то

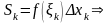
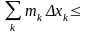
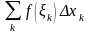
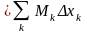
Тепер нехай , .

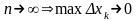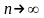Розглянемо 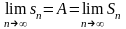, Тобто _{для будь-якого} ,

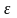
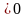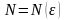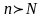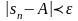знайдеться _{,що коли ,то} і _.

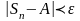Це означає, що _існує

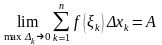
Отже, площею криволінійної трапеції називається границя, до якої наближується площа ступінчатої фігури, складеної з елементарних прямокутників, при умові, що найбільша з довжин їх основ наближується до 0.

Задача 2.

Фізичний зміст означеного інтеграла: Нехай потрібно обчислити роботу змінної по величині сили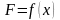 , направленої вздовж осі ox при переміщенні матеріальної точки з деякого початкового положення a в кінцеве положення _.

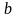Розіб’ємо відрізок на 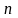частини ,

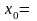
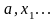
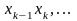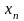
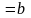
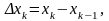
Тоді (тут 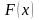можна вважати постійною. Робота сили 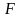на 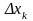наближено дорівнює при чому буде точнішим, якщо меншим.

Отже 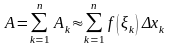або

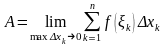
Таким чином для 1.2 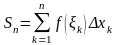називається інтегральною сумою функції . Таких сум 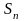– багато, оскільки все залежить від вибору .

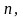Умова, що 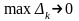означає, що існує 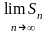,тобто, якщо 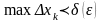, тоді , а число 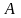називається границею інтегральної суми.

Саме така гранична називається означеним інтегралом функції на відрізку , а сама функція називається інтегрованою на відрізку .

Означення: ,

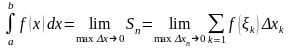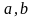- відповідно нижня та верхня границі означеного інтеграла, - відрізок інтегрування.

Отже значення 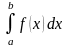дорівнює площі криволінійної трапеції, обмеженої зліва і справа прямими знизу віссю абсцис, зверху графіком функції 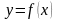. Критерій існування означеного інтеграла:

Теорема. Для будь-якої неперервної на відрізку функції існує і єдина границя відповідних інтегральних сум. Це дуже жорстка умова, наприклад, існування та єдиності .

Властивості означеного інтеграла:

1). .

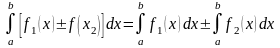Доведення:

= .

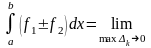
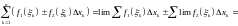
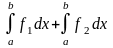2) 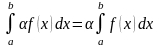(доведення аналогічне).

3). .

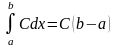Доведення: .

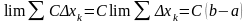4. .

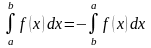Доведення:

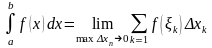
5. 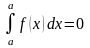(наслідок попередньої властивості).

6. , .

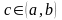Доведення:

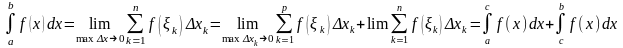
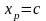
7.Якщо , .

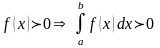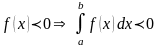Доведення тривіальне,оскільки _.

8.

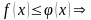
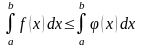
Доведення: .

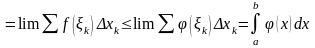9. .

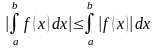Доведення основане на застосуванні відомої в математиці нерівності Коші-Буняковського: .

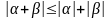10. Теорема про середнє значення означеного інтеграла:

, , _,

, , _.

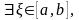
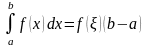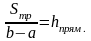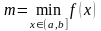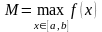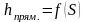
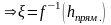11.Оцінка означеного інтеграла:

,

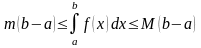
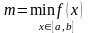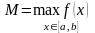
Приклад. Оцінити:

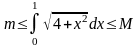
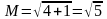, m=2 ,

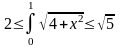
Знайти середнє значення функції

,

_.
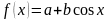
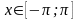
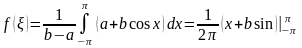
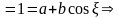
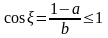
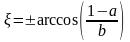