Завдання для самостійної роботи

1. Знайти масу однорідної пластини, обмеженої лініями і .

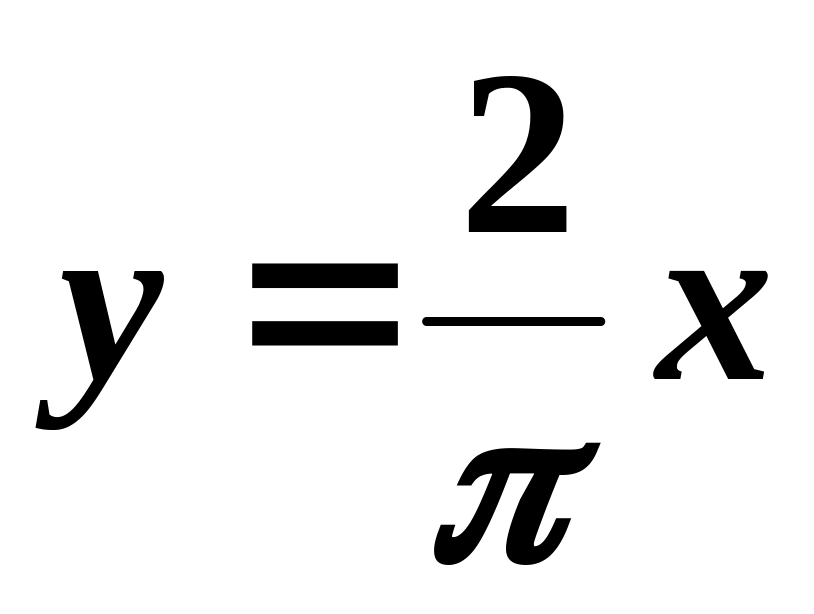2. Знайти координати центра мас пластинки, обмеженої параболою 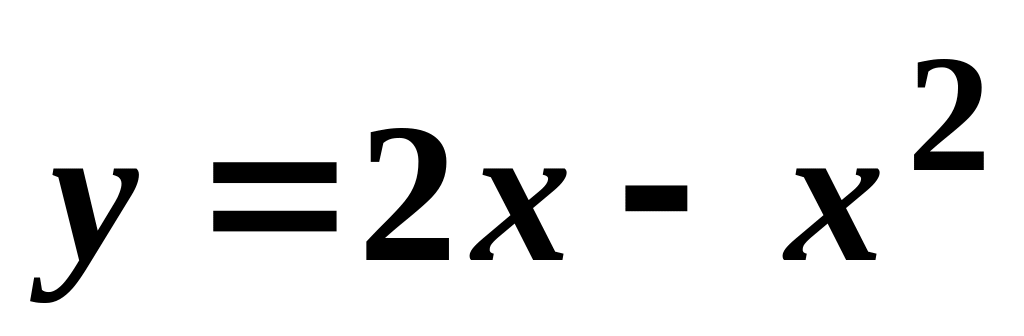та віссю .

3. Обчислити момент інерції прямокутника зі сторонами 2 і 4 відносно

точки перетину його діагоналей.

4. Знайти моменти інерції відносно вісі однорідної пластини, обмеже-

ної лініями .

5. Обчислити відцентровий момент інерції однорідної пластини, обмеже-

ної лініями .

6. Знайти момент інерції однорідної еліптичної пластини з півосями і

відносно осі .

4. Обчислення криволінійних інтегралів першого та другого роду. Формула Гріна. Умови незалежності криволінійного інтеграла від шляху інтегрування

Нехай кусково-гладка просторова крива з початком у точці і кінцем в точці , на якій визначена і неперервна функція . Інтегральною сумою розбиття дуги на елементарних частин довжини називається наступна функція , де довільна точка на елементарному відрізку розбиття.

Криволінійним інтегралом першого роду від функції по дузі називається границя (якщо вона існує) інтегральної суми розбиття при та , яка не залежить від способу розбиття дуги точками на елементи і вибору точок в частинних дугах довжини і позначається таким чином:

.

Нехай на кусково-гладкій просторовій кривій задана векторна функція , яка має проекції на осі вибраної декартової системи координат. Інтегральною сумою розбиття дуги на елементарних частин з проекціями називається функція:

де довільна точка на .

Криволінійним інтегралом другого роду від векторної функції по дузі називається скінчена границя інтегральної суми при (якщо вона існує і не залежить від способу розбиття дуги на елементи і вибору точок ). Інтеграл має вигляд:

,

де радіус вектор точки; скалярний добуток.

Для криволінійних інтегралів першого і другого роду має місце залежність:

,

де проекція вектора на вектор , який напрямлений по дотичній до дуги в точці в бік від до .

Властивості криволінійних інтегралів

1. Криволінійні інтеграли першого й другого родів не залежать від вибору

початкової точки на цьому контурі.

2. Криволінійний інтеграл першого роду не залежить від напряму обходу

шляху інтегрування.

3. Інтеграл другого роду залежить від напряму обходу дуги , а саме

.

4. Теорема про середнє. Якщо функція визначена й неперервна на

гладкій дузі (включаючи її кінці), то на цій дузі знайдеться така

точка , для якої має місце наступна рівність:

.

де довжина дуги .

Тобто криволінійний інтеграл першого роду дорівнює добутку середнього значення підінтегральної функції на довжину шляху інтегрування.

Обчислення криволінійних інтегралів першого роду за плоскою областю

I. Крива задається рівнянням , а точки і задані своїми

координатами :

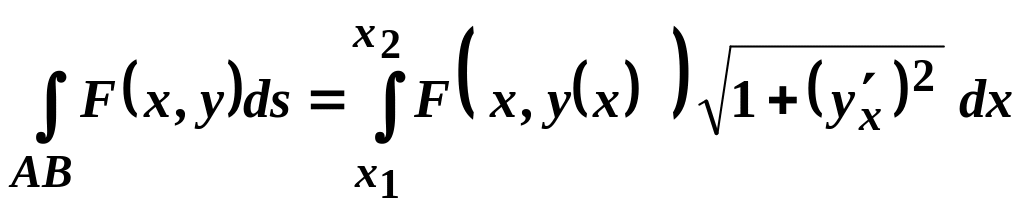. (4.1)

II. Крива задається параметричним рівнянням де .

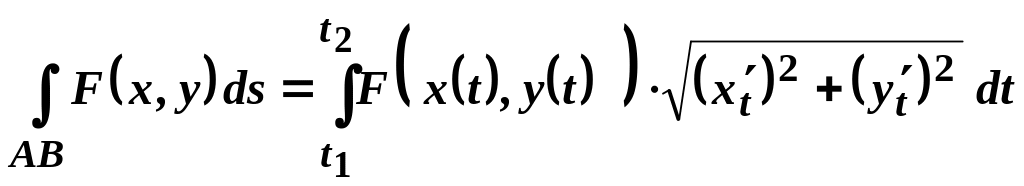. (4.2)

III. Крива задається рівнянням , де .

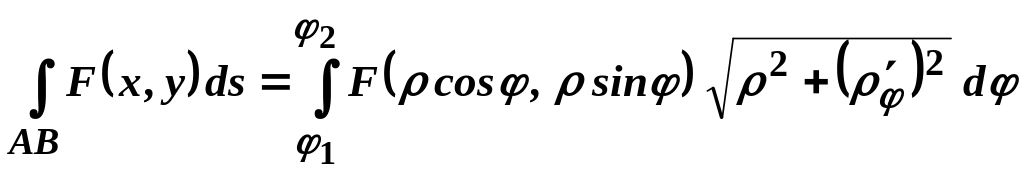. (4.3)

Обчислення криволінійних інтегралів другого роду