Завдання для самостійної роботи
Знайти загальні частинні розв’язки задач:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
9. Метод варіації довільних сталих.
Розглянемо лінійне неоднорідне диференціальне рівняння другого порядку з постійними коефіцієнтами:
,
де
будь-яка функція.
Розв’язок цього рівняння буде мати вигляд:
,
де
частинні розв’язки відповідного
диференціального однорідного рівняння,
які знаходимо за таблицею 1,
функції, які є розв’язком системи
рівнянь :
Приклад 1. Розв’язати рівняння:
.
Розв’язання.
Знайдемо розв’язок відповідного однорідного рівняння:
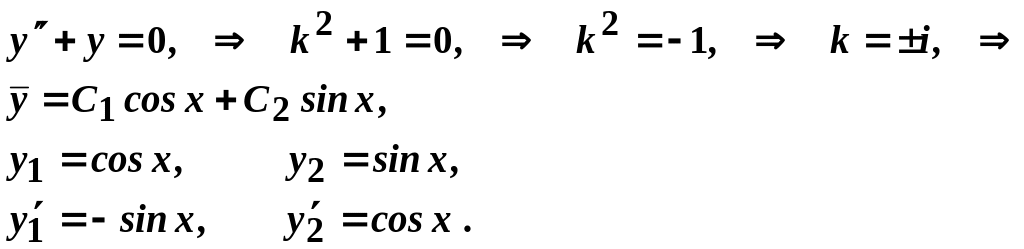
Загальний
розв’язок початкового рівняння буде
мати той же вигляд, що і загальний
розв’язок однорідного рівняння, але
та
не довільні сталі, а деякі функції, які
знайдемо із системи рівнянь:
Розв’яжемо цю систему за формулами Крамера:
,
.
Тоді
.
Дістанемо
функції
та
:
,
.
Отже, загальний розв’язок рівняння отримаємо у вигляді:
.
Приклад 2. Розв’язати рівняння:
.
Розв’язання.
Частинні
розв’язки відповідного однорідного
рівняння
з характеристичним рівнянням
мають вигляд
.
Загальний
розв’язок лінійного неоднорідного
рівняння отримаємо у вигляді
,
де невідомі функції
та
задовольняють системі алгебраїчних
лінійних рівнянь відносно
та
:
Цю систему розв’яжемо за формулами Крамера
,
,
.
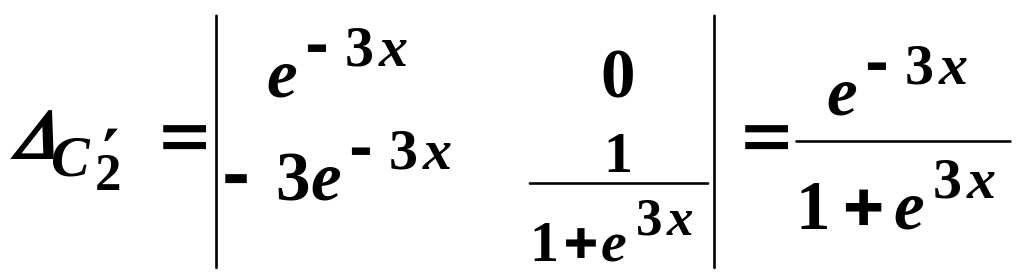Отже,
.
Проінтегруємо останні два рівняння:
.
.
Маємо під знаком інтеграла правильний раціональний дріб, який розкладемо на простіші:
.
Звідки, дістанемо :
.
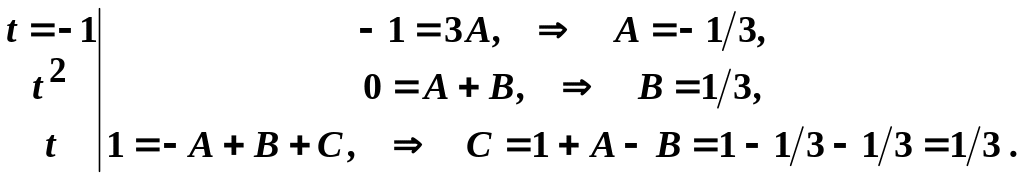
Отже,
.
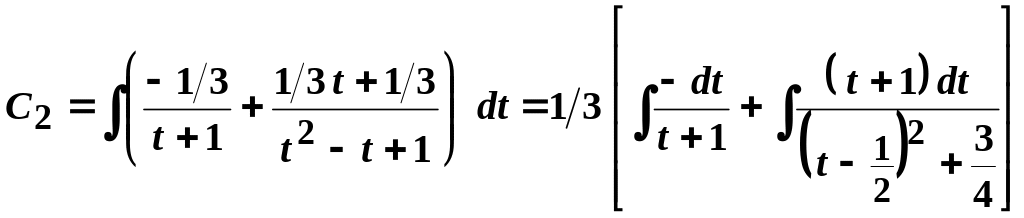Обчислимо окремо
.
.
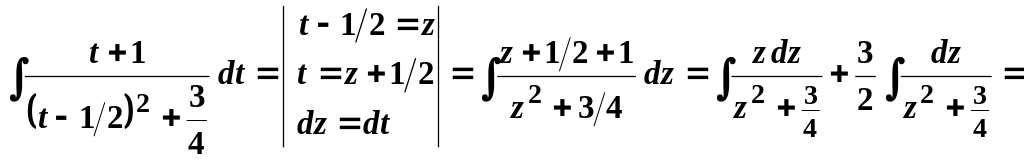
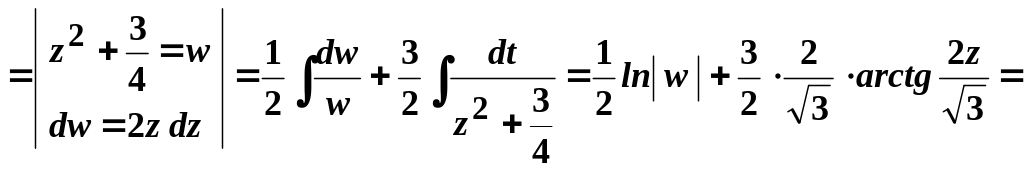
Загальний розв’язок лінійного неоднорідного рівняння дістанемо у вигляді
.
Приклад 3. Розв’язати рівняння:
.
Розв’язання.
Характеристичне
рівняння
відповідного однорідного диференціального
рівняння має корені
,
тому частинні розв’язки однорідного
рівняння
.
Загальний
розв’язок неоднорідного рівняння
шукатимемо у вигляді
.
Для знаходження невідомих функцій
та
складемо систему:
Проінтегруємо кожне з отриманих рівнянь:
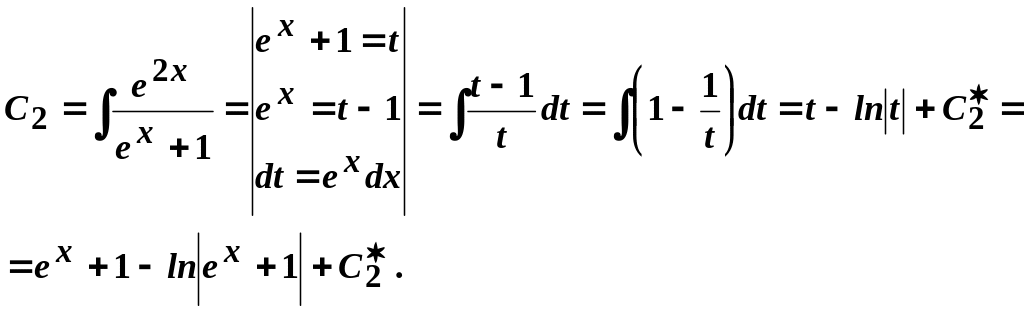
Дістанемо загальний розв’язок початкового рівняння:
.
Приклад 4. Розв’язати задачу Коші:
.
Розв’язання.
Частинні
розв’язки відповідного однорідного
рівняння
мають вигляд
.
Загальний розв’язок початкового
рівняння дістанемо у вигляді
,
де невідомі функції
та
задовольняють системі алгебраїчних
лінійних рівнянь:
або
Звідки,
;
;
.
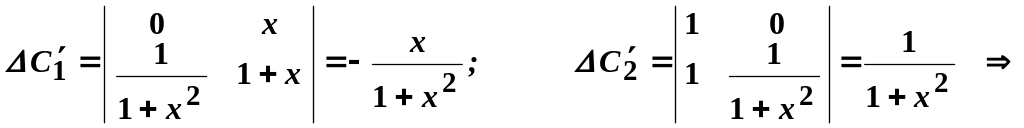
Знаходимо
,
.
Отже, загальний розв’язок неоднорідного рівняння має вигляд :
,
.
Використаємо початкові умови:
Розв’язок задачі Коші має вигляд:
.