МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНА МЕТАЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ

Т.М.КАДИЛЬНИКОВА, І.В.ЩЕРБИНА, П.Г.ХОРОШМАНЕНКО

ВИЩА МАТЕМАТИКА

В ПРИКЛАДАХ ТА ЗАДАЧАХ

Частина IV

Дніпропетровськ НМетАУ 2010

Міністерство освіти І науки україни

Національна металургійна академія україни

Т.М.КАДИЛЬНИКОВА, І.В.ЩЕРБИНА, П.Г.ХОРОШМАНЕНКО

ВИЩА МАТЕМАТИКА

В ПРИКЛАДАХ ТА ЗАДАЧАХ

Частина IV

Затверджено на засіданні Вченої ради академії

як навчальний посібник

Дніпропетровськ НМетАУ 2010

УДК 517(07)

Кадильникова Т.М., Щербина І.В., Хорошманенко П.Г. Вища математика в прикладах та задачах. Частина IV: Навч. посібник.- Дніпропетровськ: НМетАУ, 2010.- 96 с.

Наведені докладні рекомендації до вивчення дисципліни «Вища математика». Теоретичні положення супроводжуються необхідними поясненнями та ілюстраціями, а також розв’язуванням типових задач. Рекомендуються завдання для самостійної роботи.

Призначений для студентів технічних спеціальностей всіх форм навчання.

Іл.18. Бібліогр. 5 найм.

Друкується за авторською редакцією.

Відповідальний за випуск А.В.Павленко, д-р фіз.-мат. наук, проф.

Рецензенти: Т.С.Кагадій, д-р фіз.-мат. наук, проф. (НГУ) А.В.Сясєв, канд. фіз.-мат. наук, доц. (ДНУ).

© Національна металургійна академія

України, 2010

Вступ

Розв’язання задач з вищої математики часто пов’язано з багатьма складностями. Відомо, що при самостійному розв’язуванні задач студентам потрібні постійні консультації щодо способів їх розв’язування, оскільки знайти шлях до розв’язування задачі без допомоги викладача або відповідного підручника студентові не під силу. Допомогти студентам подолати ці складності, навчити їх застосовувати теоретичні знання до розв’язування задач - основне призначення цього навчального посібника.

Метою видання є надання допомоги студентам у отриманні навичок з розв’язування типових задач, користуючись наведеними теоремами та формулами, а також детально розібраними прикладами. Там, де це можливо, задачі класифікувалися за темами. До кожного нового типу подано задачі з розв’язуванням і кілька задач того самого типу для самостійного опрацювання. Основна форма навчання студентів – самостійна робота над навчальним матеріалом, яка складається з вивчення теоретичних положень за підручником, розгляду прикладів і розв’язання задач. При вивченні матеріалу за підручником треба переходити до наступного питання тільки після правильного зрозуміння попереднього, виконуючи на папері усі обчислення, навіть і ті, які пропущені у підручнику.

Завершальний етап вивчення наведених частин дисципліни «Вища математика» - складання заліків та іспитів відповідно до навчального плану, тому студент повинен пам’ятати, що тільки при систематичній самостійній роботі допомога навчального видання буде носити ефективний характер.

1. Подвійний інтеграл, його властивості. Обчислення подвійного інтеграла в декартових координатах

Нехай обмежена область площини з кусково-гладкими межами, а функція визначена і обмежена в області . За допомогою сітки кусково-гладких кривих розбиваємо область на скінченне число елементарних підобластей з площинами (рис. 1.1). Множину цих елементарних частин області назвемо розбиттям . Нехай найбільший з діаметрів елементарних областей . У кожній з елементарних областей вибирається довільна точка.

Рис. 1.1

Число ставиться у відповідність кожному розбиттю і називається інтегральною сумою розбиття .

Якщо існує границя інтегральної суми при , і якщо вона не залежить від способу розбиття області на елементарні підобласті і від вибору точок , то вона називається подвійним інтегралом від функції по області і позначається через .Таким чином,

, (1.1)

де .

Теорема. Подвійний інтеграл (1.1) існує, якщо в скінченній замкненій області , обмеженій гладким або кусково-гладким контуром, функція або неперервна, або обмежена і має розриви на скінченному числі кусково-гладких ліній.

Властивості подвійного інтеграла

1. Сталий множник можна винести за знак подвійного інтеграла:

.

2. Подвійний інтеграл алгебраїчної суми дорівнює відповідній сумі інтегралів від складових:

.

3. Якщо область розкласти на скінчене число частин, тоді подвійний

інтеграл по всій області дорівнює сумі інтегралів по всіх її частинах:

.

4. Якщо в замкненій області функції і непевні й, задо-

вольняють співвідношення , тоді справедлива нерівність:

.

5. Абсолютна величина інтеграла не перевищує інтеграла від абсолютної

величини підінтегральної функції:

.

6. Теорема про середнє. Якщо і неперервні в скінченній

замкненій області , і знакостала в , то справедлива формула:

,

де .

Обчислення подвійного інтеграла в декартових координатах

Нехай функція неперервна в прямокутнику . Вираз є елементом площі в декартових прямокутних координатах. Подвійний інтеграл від функції по області обчислюється за формулою:

. (1.2)

Якщо поміняти місцями і в (1.2), то буде справедливою рівність:

.

В останній формулі інтегрування ведеться спочатку по при сталому , а потім одержаний результат інтегрується по , тобто послідовно обчислюється два визначених інтеграли.

Нехай функція неперервна або кусково-неперервна в криволінійній області , де і функції, які неперервні на відрізку . Візьмемо область в прямокутник , де найменше значення в , найбільше значення в (рис. 1.2).

Рис. 1.2

Визначимо у цьому прямокутнику функцію такими рівностями:

Функція кусково-неперервна в прямокутнику , тому, згідно формулою (1.2), маємо:

.

Звідси отримаємо наступну формулу:

. (1.3)

Якщо область інтегрування (рис.1.3), то, змінюючи у формулі (1.3) роль і , прийдемо до аналогічної формули:

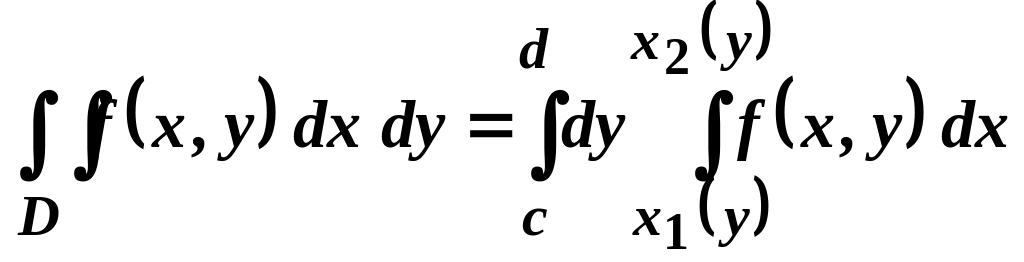. (1.4)

Рис. 1.3

Якщо область не задовольняє наведеним для (1.3) і (1.4) умовам, а саме, вертикальні й горизонтальні прямі перетинають її границю більше

ніж у двох точках, то у цьому випадку область розбивають на частини, як розглянуто вище, й, підсумовуючи одержаний результат по кожній частині, обчислюємо інтеграл по всій області.