3.3.2. Несимметричный режим работы трехпроводной трехфазной цепи

_{При неравенстве сопротивлений фаз zA ≠ zB ≠ zC фазные токи так же будут неравны между собой IA ≠ IB ≠ IC .}

_{Напряжения на фазах распределяются прямо пропорционально сопротивлениям фаз (чем больше сопротивление, тем больше падение напряжения на нем).}

_{Точка О может занять любое положение в треугольнике ABC (рис. 3.9),}

_{UA ≠ UB ≠ UC т.е. возникает «перекос фаз».}

_{Рис. 3.9. Топографическая векторная диаграмма для режима несимметричной}

_{нагрузки при соединении потребителей в звезду}

3.3.3. Обрыв одного линейного (фазного) провода в трехпроводной трехфазной цепи

_{При обрыве одного линейного провода, например, провода А (рис. 3.10, а), цепь превращается в однофазную, с последовательным соединением приемников. Если ZB = ZC, то UB = UС = 0,5UBC (рис. 3.10, б). Точка О смещается вниз и делит вектор UВС на две равные части. Если измерить напряжение между нейтралью приемника и линейным проводом А, то оно окажется равным 1,5UФ.}

_{Рис. 3.10. Схема (а) и топографическая векторная диаграмма при обрыве линейного провода (б)}

3.3.4. Короткое замыкание одной из фаз в трехпроводной трехфазной цепи

_{При коротком замыкании одной из фаз, например, фазы А, потенциал точки А становится равным потенциалу точки О, напряжение фазы А равно нулю UA = 0, следовательно, ток фазы А также равен нулю: IA = 0 (рис. 3.11, а). Фазы B и С подключены на линейное напряжение UB = UAB и UC = UСА.}

_{Рис. 3.11. Схема (а) и топографическая векторная диаграмма (б), при коротком замыкании фазы А}

3.4. Трехпроводная трехфазная цепь при соединении потребителей в треугольник

_{Если соединить начало одной фазы с концом другой, то получится соединение в треугольник (рис. 3.12, а). Как видно из схемы, линейное напряжение равно фазному напряжению Uл = UФ, а линейные и фазные токи отличаются в раз , линейный ток равен разности двух фазных токов:}

_.

_{На векторной диаграмме (рис. 3.12, б) изображены три вектора линейных напряжений , расположенных под углом 120° относительно друг друга, и векторы фазных и линейных токов. Звезда фазных токов опережает звезду линейных токов на угол 30°, но отстает от звезды фазных (линейных) напряжений на угол φ (активно-индуктивная нагрузка).}

_{Рис. 3.12. Схема соединения потребителей в треугольник (а) и векторная диаграмма цепи (б)}

_{Расчет схемы треугольника производится на основании закона Ома:}

_{; ; .}

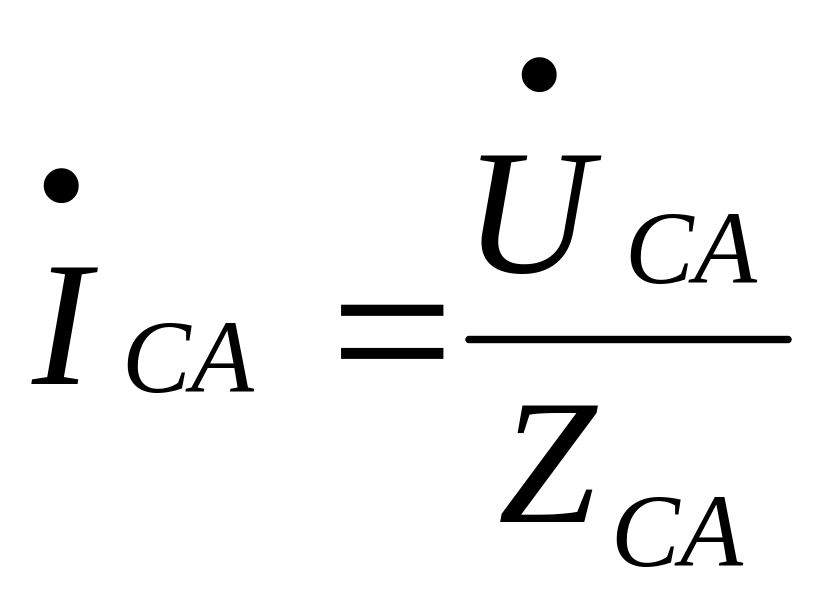_{Углы сдвига фаз определяем по известным формулам:}

_{; ; .}

3.4.1. Симметричный режим работы трехпроводной трехфазной цепи

_{Векторная диаграмма для симметричного режима работы представлена на рис. 3.12, б.}

_{Сопротивления фаз равны между собой zAB = zBC = zCA следовательно, равны фазные токи IAB = IBC = ICA и линейные токи IA = IB = IC .}