2.6. Равновесие по Нэшу в смешанных стратегиях

Нетрудно привести примеры игр, в которых равновесие по Нэшу отсутствует. В игре «Инспекция» рассматривается именно такая ситуация.

Игра 10. «Инспекция». В этой игре первый игрок (проверяемый) поставлен перед выбором – платить или не платить подоходный налог. Второй – налоговый инспектор, решает, проверять или не проверять именно этого налогоплательщика. Если инспектор «ловит» недобросовестного налогоплательщика, то взимает с него штраф и получает поощрение по службе, превышающее его издержки; в случае же проверки «исправного» налогоплательщика, инспектор, не получая поощрения, тем не менее несет издержки, связанные с проверкой. Матрица выигрышей представлена в таблице.

Игра «Инспекция»		Инспектор
		Проверять	Не проверять
Проверяемый	Нарушать	1	0
		–1	1
	Не нарушать	–1	0
		0	0

Если инспектор уверен, что налогоплательщик выберет «не платить налог», то инспектору выгодно его проверить. Вместе с тем, если налогоплательщик уверен, что его проверят, то ему лучше заплатить налог. Аналогичным образом, если инспектор уверен, что налогоплательщик заплатит налог, то инспектору не выгодно его проверять, а если налогоплательщик уверен, что инспектор не станет его проверять, то он предпочтет не платить налог. Оптимальные отклики показаны в матрице выигрышей подчеркиванием соответствующих выигрышей.

Очевидно, что ни одна из клеток не может представлять равновесие по Нэшу, поскольку ни в одной из клеток не подчеркнуты одновременно оба выигрыша.

В подобной игре каждый игрок заинтересован в том, чтобы его партнер не смог угадать, какую именно стратегию он выбрал. Этого можно достигнуть, внеся в выбор стратегии элемент неопределенности, т.е. выбирать стратегии с некоторыми вероятностями.

Те стратегии, которые мы рассматривали раньше, принято называть чистыми стратегиями. Чистые стратегии в статических играх по сути дела совпадают с действиями игроков.

Но в некоторых играх естественно ввести в рассмотрение также смешанные стратегии. Под смешанной стратегией понимают выбор чистых стратегий с некоторыми вероятностями.

Найдем равновесие по Нэшу в смешанных стратегиях в игре «Инспекция».

Обозначим через μ вероятность того, что налогоплательщик не платит подоходный налог (стратегия «нарушать»), а через ν – вероятность того, что инспектор проверяет налогоплательщика.

В этих обозначениях ожидаемый выигрыш налогоплательщика равен

u₁(μ, ν) = μ [ν (–1) + (1 – ν) 1] + (1 – μ) [ν 0 + (1 – ν) 0] = μ (1 – 2 ν),

а ожидаемый выигрыш инспектора равен

u₂(μ, ν) = ν [μ 1 + (1 – μ) (–1)] + (1 – ν) [μ 0 + (1 – μ) 0] = ν (2 μ – 1).

Если вероятность проверки мала (ν < 1/2), то налогоплательщику выгодно не платить налог, т.е. выбрать μ = 1. Если вероятность проверки велика, то налогоплательщику выгодно заплатить налог, т.е. выбрать μ = 0. Если же ν = 1/2, то налогоплательщику все равно, платить налог или нет, он может выбрать любую вероятность μ из интервала [0, 1]. Таким образом, отображение отклика налогоплательщика имеет вид:

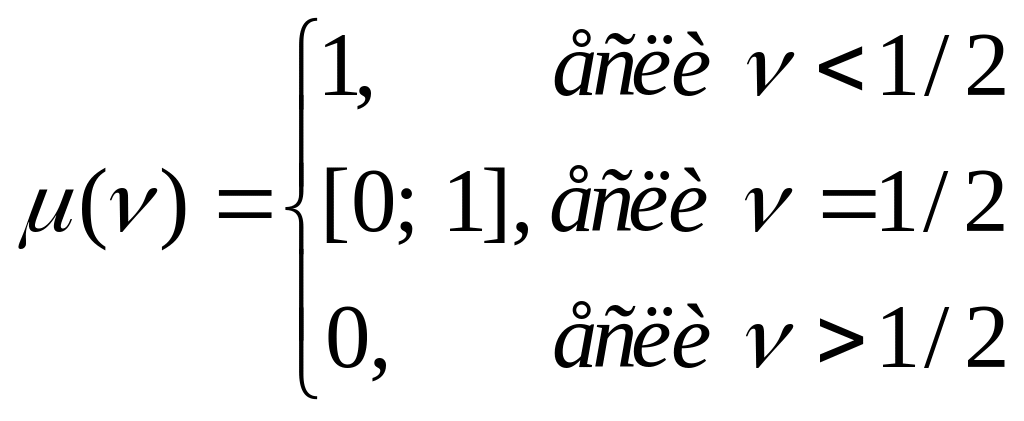
Рассуждая аналогичным образом, найдем отклик налогового инспектора:

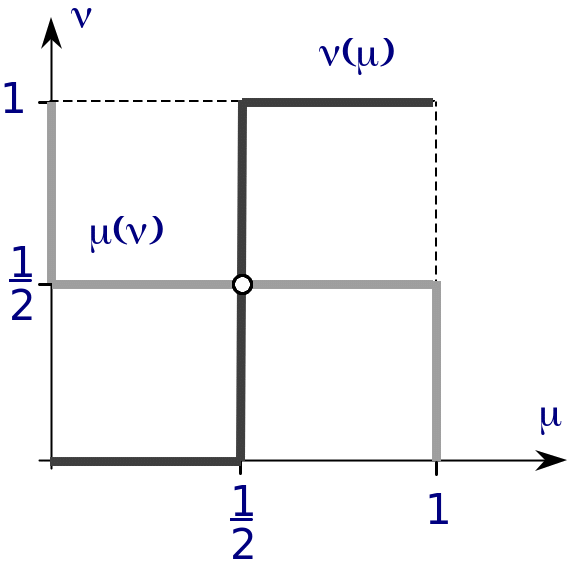
Рис. 2. Отображения отклика в игре «Инспекция»

Графики отображений отклика обоих игроков представлены на Рис. 2. По осям на этой диаграмме откладываются вероятности (μ и ν соответственно). Они имеют единственную об­щую точку (1/2, 1/2). Эта точка соответствует равновесию Нэша в смешанных стратегиях.