Фреймовая модель

Фреймовая модель ориентирована на такие знания, в которых объект, ситуация, явление описывают множествами характеристик. При этом количество объектов сравнительно невелико, но они описываются большим количеством характеристик. В этом случае база знаний состоит из фреймов, каждый из которых представляет объект или ситуацию. Он состоит из частей называемых слотами. Формально под фреймом понимают именованный кортеж двухместных кортежей:

f=<<Vi,gi>...<Vn,gn>>

f – имя фрейма

Vi,gi (кортеж от i до n) – i-тый слот

Vi – имя слота

Gi – его значение

В каждом слоте размещается характеристика, свойство, действие

Фреймы делят на 2 группы:

1) фреймы описания (фреймы-структуры)

2) ролевые фреймы (фреймы-роли)

Во фрейме структуре имена слотов – это названия характеристик или свойств объекта, а в слотах содержаться значения этих характеристик или свойств.

В ролевом фрейме в качестве имен слотов указаны вопросительные фразы, ответы на которые являются значениями слотов. Если в общем выражении для фрейма значения слотов не указаны, то фрейм называется фреймом-интенсионалом или прототипом фрейма. Фрейм с конкретными значениями слотов называется фреймом-экземпляром или фреймом-примером. В качестве значений слотов могут быть ссылки на другие фреймы и другие слоты, приказы выполнения каких-либо процедур и другие.

Алгоритмы Основные понятия

Алгоритм – конечный набор правил, шагов, позволяющий решать любую конкретную задачу из некоторого класса однотипных, при условии, что исходные данные для решения, могут изменяться в заданных пределах. Алгоритм форма представления процедурных знаний и рассматривается как основа использования программных средств для решения задач. Алгоритм – основа программирования.

Каждый из множества алгоритмов снабжается именем. Алгоритм состоит из шагов (если алгоритм А, то шаги А1,А»...). В каждом шаге одно или более действий. Шаги именуются. Имя шага состоит из имени алгоритма и порядкового номера шага. При описании действий используются специальные знаки. Знак ← означает операцию замещения (это обобщение операций подстановки и присваивания). Запись m←n означает, что значение переменной m должно быть заменено текущим значением переменной n. Знак = означает условие, которое необходимо проверить, а знак замещение означает действие, которое необходимо произвести.

Запись переменная←формула означает, что в соответствии с данной формулой должны быть произведены вычисления при текущих значениях, входящих в нее переменных. После чего переменную, стоящую слева от замещения надо заместить полученным значением. Если несколько переменных надо заместить одним и тем же значением, можно использовать сокращенную запись. Например, m←n←r. Означает, что переменные m и n следует заместить значением переменной r. Операция взаимного обмена значениями двух переменных записывается с помощью двунаправленной стрелки, например, m↔n.

В настоящее время используется несколько способов описания алгоритмов, основными из которых являются:

1) словесно-формульный (пошаговый)

2) структурный (в виде блок-схемы)

Словесно-формульное описание алгоритмов

Алгоритм записывается в виде текста по шагам, определяющим последовательность действий. Такое описание имеет определенную структуру. После имени алгоритма записывается его цель и ограничения на исходные данные. Затем следует описание шагов. Каждый шаг начинается с его имени, после которого указывается фраза (в квадратных скобках), которая как можно короче резюмирует суть этого шага. После этой фразы следует подробное описание словами и знаками тех действий, которые должны быть выполнены.Порядок действий в поле должен быть указан слева направо. После этого, если необходимо в круглых скобках записываются комментарии к шагу. Эти комментарии не являются элементами алгоритма, а приводятся лишь для удобства чтения, чтобы облегчить понимание сути шага. Пример, алгоритм Эвклида.

Алгоритм Е [Алгоритм Эвклида] Даны два целых положительных числа m и n, требуется найти их наибольший общий делитель, т.е. наибольшее целое число, которое нацело делит как m, так и n.

E1 [Нахождение остатка], r←остаток от m/n (0<=r<n)

E2 [Это 0?], r=0, алгоритм заканчивается, в n искомое число m←n, n←r

E3 [Замещение]

E1

Структурное описание алгоритма

В этом случае алгоритм изображается ориентированной бинарной семантической сетью. Блок-схема – это частично однородная сеть. Блок-схема – это удобное для человека графическое изображение алгоритма в виде плоских геометрических фигур (их называют блоками или вершинами), соединенных направленными линиями (их называют дугами). В ней дуги, соответствующие отношению безусловного следования, не отмечаются. Отмечаются лишь дуги, исходящие из вершин, в которых проверяются условия. Такие дуги соответствуют отношению условного следования. В такой сети в вершинах (блоках) записываются шаги алгоритма, а дуги показывают последовательность выполнения этих шагов. В блок-схеме присутствуют вершины разного типа.

Основными из них являются:

1. вершины начала и окончания (изображаются овалами). У вершины–начала нет входящих дуг, у нее есть лишь 1 исходящая, направленная к вершине, с которой начинается алгоритм. У вершины – окончания нет исходящих дуг и может быть несколько входящих.

2. вершины-действия (изображаются прямоугольниками), соответствуют шагам, в которых выполняются действия. Такая вершина может иметь несколько входящих дуг и только одну исходящую.

3. вершины-условия (изображаются ромбами) соответствуют шагам, в которых проверяются условия, каждая такая вершина может иметь несколько входящих дуг и не менее двух исходящих. Каждая из исходящих дуг отмечается результатом проверяемого условия и направлена к той вершине, которая должна выполняться при получении этого результата. Если в качестве проверяемого условия указано логическое выражение, то одна из исходящих дуг соответствует отношению следования при условии, что проверяемое логическое выражение истинно. Такая дуга отличается меткой «да». Другая исходящая дуга соответствует отношению следования при условии, что проверяемое логическое выражение ложно. Такая дуга отмечается меткой «нет».

4. вершины ввода/вывода (изображаются параллелограммами) соответствуют шагам, в которых выполняются ввод или вывод данных.

5. вершины-узлы, обозначают объединение нескольких входящих дуг, изображаются точками или кругами небольшого размера.

Блок- схема может быть краткой и подробной (укрупненной). В краткой блок-схеме в вершинах указываются только наименование и основная суть шагов. Например:

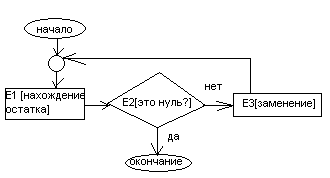
В подробной блок схеме в вершинах указывается полное описание шагов

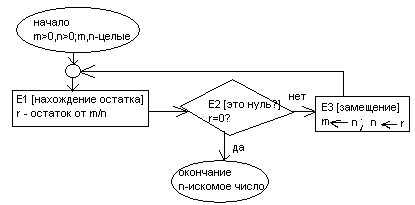
Блок–схема первого типа сопровождает пошаговое описание алгоритма, а блок-схема второго может его заменить. Блок-схема – это наиболее рациональный способ, обеспечивающий понимание логики алгоритма, но перегружать ее текстами не рекомендуется, поэтому сложные алгоритмы обычно описывают в пошаговой форме, дополняя это описание краткой блок-схемой.

Элементарные алгоритмические структуры

Любой алгоритм представляет собой комбинацию трех алгоритмических структур: линейной, ветвящейся и циклической.

Линейная структура – это процесс, в котором операции выполняются последовательно в порядке их описания. Вершины, отображающие эти действия, располагаются в линейной последовательности. Такие процессы имеют место, например, при вычислении арифметических выражений, когда имеются конкретные числовые данные и над ними выполняются соответствующие условию задачи действия. Например, вычисление

можно представить следующей линейной структурой:

В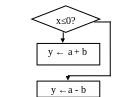 етвящаяся структура – это процесс, для реализации которого предусмотрено несколько направлений (ветвей). Каждое отдельное направление является отдельной ветвью. Направление ветвления выбирается в соответствии с результатом проверяемого условия, если условием является логическое выражение, то предполагается альтернативный выбор. Такой ветвящийся процесс включает в себя две ветви и называется простым или альтернативным. Например,

Эта структура реализует вычисление:

^y={

Если процесс предполагает более двух ветвей, то он называется сложным. Например,

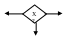
Циклическая структура – это процесс, содержащий цикл. Цикл – это последовательность многократно повторяющейся группы действий. Например,

В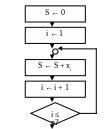 описании цикла можно выделить следующие этапы:

1) подготовка (инициализация) цикла включает действия по подготовке значений параметров, участвующих в действиях цикла. В данном примере первые два действия.

2) выполнение (тело цикла) включает действия, составляющие цикл (S ← S + x_i )

3) модификация параметров включает действия, изменяющие значения тех параметров, от которых зависит условие окончания цикла (i ← i + 1).

4) проверка условия окончания цикла (i ≤ n?).

Цикл называется детерминированным, если число повторений тела цикла заранее известно. Цикл называется итерационным, если число повторений тела цикла заранее не известно, а зависит от переменных, участвующих в вычислениях.

Различают цикл с нижним окончанием или с постусловием (условие проверяется после тела цикла) и цикл с верхним окончанием или с предусловием (условие проверяется перед телом цикла). Отличие заключается в том, что в первом случае тело цикла обязательно выполняется по крайней мере один раз, а во втором – может не выполниться ни разу.