Содержание

Тема 1 Средние величины и показатели вариации…………………..…..3

Задание 0………………………………………………………………..…..3

Задание 1……………………….……………………………………….…..4

Задание 2……………………………………………………………………4

Тема 2 Относительные величины…………………………………..…….6

Задание 3…………………………………………………………….…..….6

Тема 3 Ряды динамики………………………………………….…….……7

Задание 4…………………………………………………………………....7

Тема 4 Индексы………………………………………………………...…12

Задание5…………………………………………………………………...12

Тема 5 Выборочные наблюдения………………………………………...13

Задание 6…………………………………………………………………..13

Тема 6 Статистика населения…………………………………….………14

Задание 7……………………………………………………………….….14

Тема 7 Система национальных счетов…………………………………..20

Задание 8…………………………………………………………………..20

Список использованной литературы…………………………………….25

Тема 1 Средние величины и показатели вариации

Задание 0

Кредиторская задолженность предприятий района за отчетный период характеризуется данными, тыс. руб.: 40, 60, 80, 50, 74, 90, 120, 45, 70, 92, 100, 52, 67, 83, 70, 74, 63, 75, 85, 110.

1. Постройте ряд распределения предприятий по размеру кредиторской задолженности, образовав 4 группы с разными интервалами.

2. По данным ряда распределения определите:

а) структуру предприятий по размеру кредиторской задолженности;

б) средний размер кредиторской задолженности.

Решение:

а) при построении ряда с равными интервалами величина интервала h определяется по формуле ,

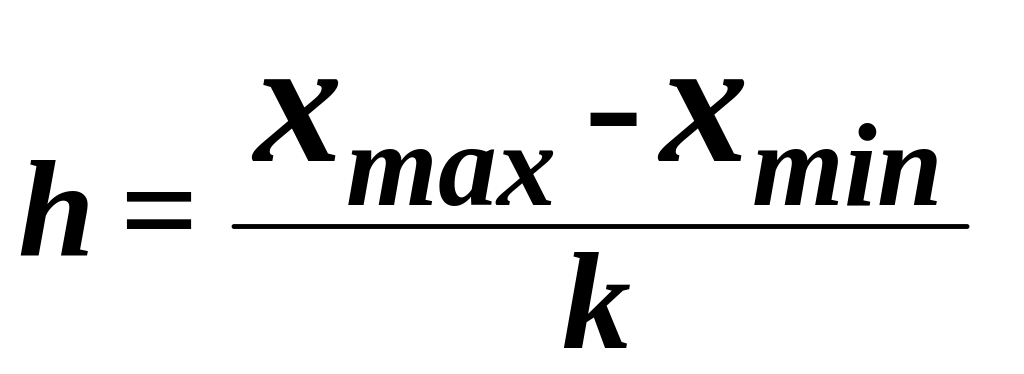где – наибольшее и наименьшее значения признака в исследуемой совокупности,

k - число групп интервального ряда.

h = (120 - 40) / 4 = 20

Группы	Число	В%	Середина интервала, Хср
40-60	4	20	50
60-80	8	40	70
80-100	5	25	90
100-120	3	15	110

б) определим средний размер кредиторской задолженности

Хср = ∑Хi * f / ∑f

Xср = (50 * 4 + 70 * 8 + 90 * 5 + 110 * 3) / 20 = 77 (тыс. руб.)

Задание 1

По двум торговым фирмам имеются следующие данные о товарообороте магазинов за отчетный год:

Район	Торговая фирма 1		Торговая фирма 2
	Средний товарооборот на один магазин, млн. руб. Х	Число магазинов,f	Средний товарооборот на один магазин, млн. руб., Х	Число магазинов,f
А	20,0	240	22,0	5500
В	22,0	260	23,0	6900
С	24,0	300	25,0	8000

Вычислите средний товарооборот на один магазин:

а) по торговой фирме 1;

б) по торговой фирме 2

Сравните полученные показатели.

Решение:

а) определим средний товарооборот на один магазин по торговой фирме 1, с помощью средней взвешенной:

Хср = ∑Х * f / ∑f

Хср = (20,0 * 240 + 22,0 * 260 + 24,0 * 300) / 800 = 22,15 (млн. руб.)

б) определим средний товарооборот на один магазин по торговой фирме 2, с помощью средней взвешенной:

Хср = (22,0 * 5500 + 23,0 * 6900 + 25,0 * 8 000) / 20400 = 23,52 (млн. руб.)

Вывод: средний товарооборот на один магазин по торговой фирме 2 выше, чем по торговой фирме 1.

Задание 2

Основываясь на ниже приведенных данных, определите: среднюю величину анализируемого признака; размах вариации; среднее линейное отклонение; среднее квадратическое отклонение; дисперсию; коэффициент вариации; моду и медиану.

Определите средний возраст студентов одной группы по данным, приведенным в таблице, показатели его вариации, моду и медиану.

Возраст студентов, лет	18	19	20	21	22	Всего
Число студентов	22	11	5	7	15	60

Решение:

1. определим средний возраст студентов:

Хср = ∑Х * f / ∑f

Хср = (18 * 22 + 19 * 11 + 20 * 5 + 21 * 7 + 22 * 15) / 60 = 19,7 (лет)

2. определим размах вариации

R = Xmax – Xmin

R = 22 – 18 = 4

3) определим среднее линейное отклонение:

Число студентов	Среднее значение	Индивидуальное отклонение
22	12	10
11	12	│-1│
5	12	│-7│
7	12	│-5│
15	12	3
итого		26

Л = 26 / 5 = 5,2

4) определим среднее квадратическое отклонение

σ = √((18 – 19,7)² * 22 + (19 – 19,7)² * 11 + (20 – 19,7)² * 5 + (21 – 19,7)² * 7 + (22 – 19,7)² * 15) / 60 = √2,68 = 1,64

5) определим дисперсию:

σ² = (1,64)² = 2,68

6) коэффициент вариации:

V = σ * 100 / x_ср

V = 1,64 * 100 / 19,7 = 8,32

7) определим моду:

Модой в статистике называют значение признака (варианта), которое наиболее часто встречается в вариационном ряду. Наибольшую частоту (22) в рассматриваемом ряду имеет варианта 18 (возраст студентов), следовательно, она и будет модой: Мо = 18.

8) определим медиану:

Медианой для этого ряда будет значение варианты 20, что можно записать как Ме = 20.