Обработка ведомости вычисления координат вершин теодолитного хода.

Увязка углов хода. Значения измеренных углов записываем в графу 2 таблицы: «Ведомость вычисления координат», в графу 4 записываем исходный дирекционный угол αо и конечный дирекционный угол αп.

Вычисляем сумму ∑ βпр измеренных углов хода

∑ βпр = 330º 59,2' + 50º 58,5' + 161º 20,0' + 79º 02,8' + 267º 08,2' = 889º 28,7'

3. Определяем теоретическую сумму углов ∑βт

∑ βТ = αо - аn + 180 º n = 14º 37,2´ - 25º 10,0´ + 180º · 5 = 889º 27,2 ';

Находим угловую невязку.

ƒβ = ∑ βпр - ∑ βТ = 889º 28,7' - 889º27,2' = 0º 01,5 ';

если невязка ƒβ не превышает допустимой величины ƒβ доп = ±1' , то ее распределяют с обратным знаком поровну на все углы хода с округлением значении поправок до десятых долей минут.

ƒβ доп = ±1'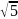 = ± 0º 02,2'

ƒβ = 0º 1,5' < ƒβ доп = ± 2,2'

ƒβ = 0º 1,5' / 5(вершин) = 0,3 , поскольку ƒβ < ƒβ доп, то получим - 0,3 на каждый угол.

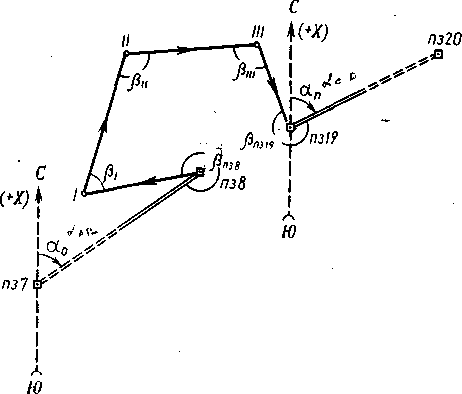
Рис. 2. Схема теодолитно-высотного хода съемочного обоснования.

Зная угловую невязку, вычисляем исправленные углы и результаты записываем в графу № 3.

330º 59,2' – 0,3 = 330º 58,9';

50º 58,5' – 0,3 = 50º 58,2';

161º 20,0' – 0,3 = 161º 19,7';

79º 02,8' – 0,3 = 79º 02,5';

267º 08,2' – 0,3 = 267º 07,9';

∑ βпр = 330º 58,9' + 50º 58,2' + 161º 19,7' + 79º 02,5' + 267º 07,9' = 889º 27,2'

ƒβ = ∑ βпр - ∑ βТ = 889º 27,2' - 889º 27,2' = 0º 0';

Вычисляем дирекционные углы и румбы сторон хода. По исходному дирекционному углу αо и исправленным значениям углов β хода по формуле для правых углов вычисляем дирекционные углы всех остальных сторон. Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус правый (исправленный) угол хода, образованный этими сторонами.

αпз 8-1 = αо + 180º + 360º - βпз 8 = 14º 37,2´ + 180º + 360º - 330º 58,9' = 223º 38,3';

αI = αпз 8-1 + 180º - βI = 223º 38,3'+ 180º - 50º 58,2' = 352º40,1';

αII = αI + 180º - βII = 352º40,1' + 180º - 360º - 161º 19,7' = 11º 20,4';

αIII = αII + 180º - βIII = 11º 20,4' + 180º - 79º 02,5 ' = 112º 17,9';

αn = αIII + 180º - β ПЗ 19 = 112º 17,9'+ 180º - 267º 07,9' = 25º 10,0'

С помощью таблицы: «Перевод дирекционных угол в румбы. Знаки приращений координат.» находим значение румбов и записываем в графу 5.

СЗ 360 - 352º40,1' = 7º 19,9΄;

СВ 11º 20,4' = 11º 20,4';

ЮВ 180 - 112º 17,9' = 67º 42,1΄;

ЮЗ 223º 38,3' - 180º = 43º 38,3΄;

Вычисление приращений координат. Вычислим по формулам:

∆х = d cos α = ± d cos α; ∆у = d sin α = ± d sin α;

∆хI = 263,02 cos 43º 38,3΄ = 263,02 * 0,724 = -190,43;

∆уI = 263,02 sin 43º 38,3΄ = 263,02 * 0,690 = -181,48;

∆хII = 239,21 cos 7º 19,9΄ =239,21 * 0,992 = 237,3;

∆уII = 239,21 sin 7º 19,9΄ = 239,21 * 0,127 = -30,38;

∆хIII = 269,80 cos 11º 20,4' = 269,80 * 0,981 = 264,67;

∆уIII = 269,80 sin 11º 20,4' = 269,80 * 0,196 = 52,88;

∆хIV = 192,98 cos 67º 42,1΄ = 192,98 * 0,379 = -73,14;

∆уIV = 192,98 sin 67º 42,1΄ = 192,98 * 0,925 = 178,5;

Полученные данные записываем в графу 7 и 8 таблицы. В каждой из граф складываем все вычисленные значения ∆х и ∆у, находя практические суммы приращения координат ∑∆хпр. и ∑∆упр.

∑∆xпр. = -190,43 + 237,06 + 264,67 - 73,14 = 238,16

∑∆yпр. = -181,48 - 30,38 + 52,88 + 178,5 = 19,52

Вычисляем теоретические суммы приращений координат ∑∆хт. и ∑∆ут., как разность абсцисс и ординат конечной точкой ПЗ 19 и начальной точкой ПЗ 8 точек хода:

∑∆хт. = х кон – х нач, ∑∆ут. = у кон – у нач,

∑хт = 224,4 – (-14,02) = 238,42

∑ут = 647,11 - 627,98 = 19,13

Вычисляем абсолютную и относительную невязки хода; увязка приращений координат. Сначала вычисляем невязки ƒх и ƒу в приращениях координат по осям х и у:

ƒх = ∑∆хпр - ∑хт.; ƒу = ∑∆упр. - ∑ут.;

ƒх = 238,16 - 238,42 = -0,26

ƒy = 19,52 – 19,13= 0,39

Вычисляем невязки приращений координат:

v = (ƒх/р)D; v = (ƒy/р)D

v = (0,26/965,01) х 263,02 = 0,07; v = (0,39/965,01) х 263,02 = 0,11;

v = (0,26/965,01) х 239,21 = 0,06; v = (0,39/965,01) х 239,21 = 0,1;

v = (0,26/965,01) х 269,8 = 0,07; v = (0,39/965,01) х 269,8 = 0,11;

v = (0,26/965,01) х 192,98 = 0,05; v = (0,39/965,01) х 192,98 = 0,08;

Абсолютную линейную невязку ∆Р хода вычисляют по формуле:

∆Р=

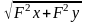
и записываем с точностью до сотых долей метра.

∆Р = 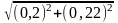≈ 0,3 м.

∆Р/Р = 0,3/965,01 = 1/3216 < 1/2000

Определяем координаты вершин и записываем в графы 12 и 11.

х_I = х_ПЗ8 + ∆х_ПЗ8-I = -14,02 – 190,36 = -204,38 y_I = y_ПЗ8 + ∆y_ПЗ8-I = 627,98 – 181,59 = 446,39

х_II = х_I + ∆х_I-II = -204,38 + 237,36 = 32,98 y_II = y_I + ∆y_I-II = 446,39 – 30,48 = 415,91

х_III = х_II + ∆х_II-III = 32,98 + 264,74 = 297,72 y_III = y_II + ∆y_II-III = 415,91 + 52,77 = 468,68

х_ПЗ19 = х_III + ∆х_III-ПЗ19 = 297,72 – 73,09 = 224,63 y_ПЗ19 = y_III + ∆y_III-ПЗ19 = 468,68 + 178,42 = 647,1