44. Модели межотраслевого баланса (моб). Модель Леонтьева.

Балансовые модели основываются на понятии межотраслевого баланса, те равенства между количеством выпускаемой продукции и совокупной потребностью в этом продукте. Цель балансового анализа – ответить на вопрос: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, с другой – как потребитель продукции и своей, и произведенной другими отраслями.

Рассмотрим n отраслей промышленности, каждая из которых производит свою продукцию. Часть идет на внутрипроизводственное потребление данной отраслью и другими отраслями, другая часть предназначена для конечного (не производственного) потребления.

Пусть

- общий валовой объем продукции i –той отрасли (i=1,2,..,n).

– объем продукции i-той отрасли, потребленной j-той отраслью в процессе производства (i,j=1,2,..,n).

– объем конечного продукта i-той отрасли для непосредственного потребления.

Уравнение соотношения баланса:

.

Будем рассматривать стоимостной межотраслевой баланс.

Коэффициенты прямых затрат

, показывающие затраты i-той отрасли на производство единицы продукции j-той отрасли.

На некотором промежутке времени коэффициенты будут постоянными. Это означает линейную зависимость материальных затрат от валового выпуска:

вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.

.

Обозначим

.

X – матрица-столбец валового выпуска,

Y – матрица-столбец прямых затрат,

A – матрица прямых затрат.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.

.

Если матрица невырожденная, т.е. , то .

Матрица называется матрицей полных затрат или матрица Леонтьева.

Чтобы выяснить экономический смысл элементов матрицы , будем задаваться единичными векторами конечного продукта .

Тогда

.

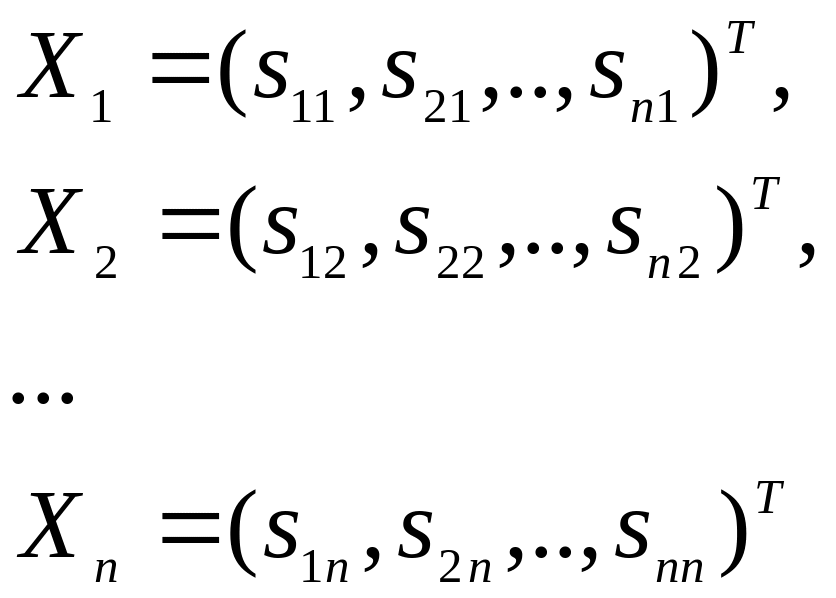Следовательно, каждый элемент s_ij матрицы S есть величина валового выпуска продукции i-той отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-той отрасли Значения должны быть неотрицательны при неотрицательных значениях и , где .

Матрица называется продуктивной, если для любого вектора существует решение . В этом случае и модель Леонтьева называется продуктивной. Матрица А продуктивна, если для любых и и существует j, такой что .

45. Модели установления равновесной цены. Поведение фирмы на конкурентном рынке

Существует много моделей установления равновесной цены на рынке одного товара. Рассмотрим две наиболее известные модели: «паутинообразную» модель с дискретным временем и модель Эванса с непрерывным временем.

Паутинообразная модель

Функция спроса на товар, полученная на основе теории полезности, является убывающей функцией цены. В свою очередь при рассмотрении теории фирмы было показано, что функция предложения однопродуктовой фирмы, полученная при максимизации прибыли, является возрастающей функцией цены.

Рассмотрим рынок с одним единственным продуктом, спрос который характеризуется убывающей функцией совокупною Ф(р), а предложение — возрастающей функцией совокупного приложения ψ (р). Естественно предположить, что эти функции непрерывны для всех р>0. Кроме того, будем считать, что

lim Ф(p) = 0; lim ψ(р)=0,

Состояние равновесия характеризуется равенством спроса и предложения:

Ф(p)= ψ (p) (1)

причем в силу сделанных предположений уравнение (1) имеет единственное решение р^ɛ, так что состояние равновесия Ф(p^ɛ) = ψ (p^ɛ) = x^ɛ единственно.

Н а рис. 5.1 показаны графики функций спроса и предложения на сделанных предположениях.

Паутинообразная модель позволяет реализовать процесс «нащупывания» равновесной цены. Пусть в начальный момент времени установлена начальная цена p₀, при этом спрос оказался меньше предложения, т.е.

Ф(Р₀)< ψ(Р₀), тогда понижаем цену до уровня, при котором спрос равен предложению при первоначальной цене:

Ф (p1) = ψ (p₀)- При новой цене р₁ спрос превышает предложение Ф(p1)> ψ (p1). поэтому повышаем цену до уровня р₂, при котором Ф(p2)= ψ (p1) и так далее.

Таким образом, как видно из рис. выше, процесс, описываемый рекуррентным соотношением Ф(p_t) < ψ (p_t-1). t = 1,2, ....сходится.

На рис. выше функция Ф(р) - выпуклая, а функция ψ (р) - вогнутая. Если бы ψ (р) была выпуклой функцией, то описанный процесс был бы расходящимся, хотя имелось бы единственное решение уравнения (1).

При паутинообразной модели с запаздывающим предложением при определении цены производитель оринтируется на спрос в прошлом периоде. Производятся аналогичные действия и получаем формулу:

Ф(p_t) = ψ (p_t+1).

Модель Эванса

В модели рассматривается рынок одного товара. Время t считается непрерывным. Обозначим через d=d(t)=Ф[p(t)], s=s(t)= ψ [p(t)] совокупные спрос и предложение в момент t, а через р = p(t) - цену товара в этот момент.

В модели постулируется, что спрос и предложение являются линейными функциями цены:

Ф (р) = а — bр, а> 0, b>0 (спрос с ростом цены убывает);

Ф ( р) = +p, а > 0,  > 0 (предложение с ростом цены растет).

Кроме того, естественно считать a> (при нулевой цене спрос превышает предложение!).

Основное предположение модели состоит в том, что изменение цены пропорционально превышению спроса над предложением:

∆p =γ (d-s)∆t, γ>0. (5.1.2)

Согласно предположению (5.1.2) взаимодействие потребителей и производителей происходит таким образом, что отражающая это взаимодействие цена непрерывно приспосабливается к ситуации на рынке: в случае превышения спроса над предложением возрастает, в противном случае падает.

Используя сделанные предположения, приходим к следующему дифференциальному уравнению относительно цены:

(5.1.3)

Это уравнение имеет стационарную (равновесную) точку

(5.1.4)

Из (5.1.3) видно, что при p₀ < p^ɛ, , а при p₀ > p^ɛ, , поэтому

lim_t--00p(t)= p^ɛ

(в первом случае цена достигает равновесного значения, возрастая; а во втором случае — убывая, при этом равновесная цена р₀ совершенно не зависит от начальной р₀). Равновесная цена р^ɛ - абсцисса точки пересечения прямых спроса и предложения, т.е. при такой цене спрос равен предложению.

Эти выводы получены без непосредственного решения уравнения (5.1.3). Разумеется, они будут точно такими же, если напрямую использовать решение этого уравнения

Д искретный аналог модели Эванса представлен на рис. ниже. На этом рисунке изображены прямые совокупного спроса и предложения и показан механизм возникновения последовательности p_n, возрастающей от начальной цены р₀, при которой спрос не равен пред­ложению, к равновесной цене р^ɛ, при которой спрос равен предложению. Все время разбито на интервалы длиной ∆t цена в момент t = n∆t,