28. Понятие регрессии. Определение параметров уравнения связи
Регрессия в статистике — статистическая зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин; введена Фрэнсисом Гальтоном (1886).
Уравнением связи называется уравнение регрессии, а анализ, производимый с помощью уравнения регрессии, называется регрессионным анализом.
После установления вида функции для модели связи определяются параметры уравнения регрессии а0 и а1. Параметры уравнения регрессии определяются методом наименьших квадратов, суть которого состоит в том, что теоретическая линия регрессии должна быть проведена так, чтобы сумма квадратов отклонений эмпирических данных от теоретических была величиной минимальной.
Параметр а1называется коэффициентом регрессии и показывает изменения результативного признака при изменении факторного признака на единицу. Параметр а0 не имеет экономического содержания, так как может принимать отрицательные значения.
29. Нелинейная корреляция. Показатели тесноты связи: эмпирическое корреляционное отношение, коэффициент детерминации
Нелинейная корреляция - корреляция, при которой отношение степени изменения одной переменной к степени изменения другой переменной является изменяющейся величиной.
Уравнение нелинейной регрессии дополняется показателем корреляции – индексом корреляции.
Для любых моделей, в том числе и нелинейных, показатель корреляции вычисляется так:
Если модель нелинейная относительно объясняющей переменной приводится к виду парной или множественной регрессии, то линейный коэффициент корреляции совпадает с индексом корреляции.
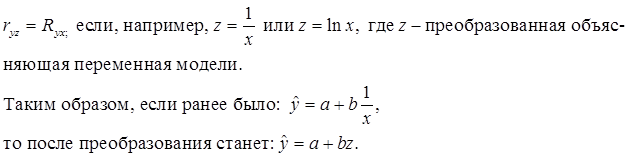
30. Множественная корреляция. Уравнение множественной регрессии
Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Например, агент по продаже недвижимости мог бы вносить в каждый элемент реестра размер дома (в квадратных футах), число спален, средний доход населения в этом районе в соответствии с данными переписи и субъективную оценку привлекательности дома. Как только эта информация собрана для различных домов, было бы интересно посмотреть, связаны ли и каким образом эти характеристики дома с ценой, по которой он был продан. Например, могло бы оказаться, что число спальных комнат является лучшим предсказывающим фактором (предиктором) для цены продажи дома в некотором специфическом районе, чем "привлекательность" дома (субъективная оценка). Могли бы также обнаружиться и "выбросы", т.е. дома, которые могли бы быть проданы дороже, учитывая их расположение и характеристики.
Специалисты по кадрам обычно используют процедуры множественной регрессии для определения вознаграждения адекватного выполненной работе. Можно определить некоторое количество факторов или параметров, таких, как "размер ответственности" (Resp) или "число подчиненных" (No_Super), которые, как ожидается, оказывают влияние на стоимость работы. Кадровый аналитик затем проводит исследование размеров окладов (Salary) среди сравнимых компаний на рынке, записывая размер жалования и соответствующие характеристики (т.е. значения параметров) по различным позициям. Эта информация может быть использована при анализе с помощью множественной регрессии для построения регрессионного уравнения в следующем виде: Salary = .5*Resp + .8*No_Super
Как только эта так называемая линия регрессии определена, аналитик оказывается в состоянии построить график ожидаемой (предсказанной) оплаты труда и реальных обязательств компании по выплате жалования. Таким образом, аналитик может определить, какие позиции недооценены (лежат ниже линии регрессии), какие оплачиваются слишком высоко (лежат выше линии регрессии), а какие оплачены адекватно.
В общественных и естественных науках процедуры множественной регрессии чрезвычайно широко используются в исследованиях. В общем, множественная регрессия позволяет исследователю задать вопрос (и, вероятно, получить ответ) о том, "что является лучшим предиктором для...". Например, исследователь в области образования мог бы пожелать узнать, какие факторы являются лучшими предикторами успешной учебы в средней школе. А психолога мог быть заинтересовать вопрос, какие индивидуальные качества позволяют лучше предсказать степень социальной адаптации индивида. Социологи, вероятно, хотели бы найти те социальные индикаторы, которые лучше других предсказывают результат адаптации новой иммигрантской группы и степень ее слияния с обществом. Заметим, что термин "множественная" указывает на наличие нескольких предикторов или регрессоров, которые используются в модели.