Входной ток совпадает по фазе с входным напряжением. По закону Ома:

Действующее значение входного тока:

3.1.4 Определение добротности резонансного контура:

3.1.5 Определение полосы пропускания резонансного контура:

c^-1

4. Расчет установившихся значений напряжений и токов в электрических цепях при несинусоидальном воздействии

1. Рассчитать законы изменения тока i_вх(t) и напряжения u_вых(t) частотным методом, представив напряжение u_вх(t)=u₄(t) в виде ряда Фурье до 5-й гармоники: u_вх(t)= (4U_m/k)sin kt, где k – целое нечетное число.

Входное напряжение задано формулой (ряд Фурье)

,

где k = 1, 3, 5.

Входное воздействие можно записать в виде

K			,º
1	0.613	-0.074	-4.22
3	0.601	-0.026	-1.5
5	0.6	-0.015	-0.9

Рассчитаем выходное напряжение частотным методом

Рассчитаем функцию зависимости входного сопротивления от k :

K
1	0.01	4.45
3	0.01	1.6
5	0.01	0.9

Следовательно,

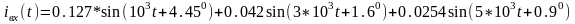
Имеем:

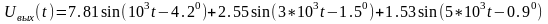
3.2 Построение графиков напряжения и тока

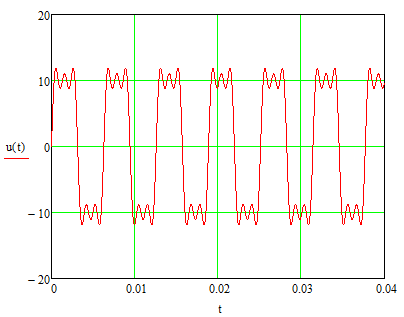
Рис. 16. График входного напряжения

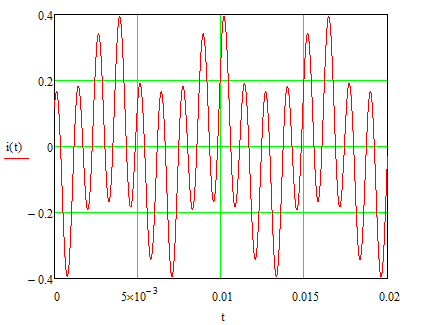
Рис. 17. График входного тока

Рис. 18. График выходного напряжения

4.3 Определение действующих значений несинусоидальных токов, активной мощности, реактивной мощности, коэффициента формы кривых

Вычисления проводим, исходя из того, что квадрат действующего значения величины равен сумме квадратов действующих значений всех трех гармоник.

Действующее значение входного тока:

А

Действующее значение выходного напряжения:

В

Действующее значение входного напряжения:

В

Активная мощность равна

P= I_вх *U_{вх*cos(Δφ}), где k=1,3,5

Полная (кажущаяся) мощность равна

S= I_вх *U_вх=

Реактивная мощность Q определяется из соотношения:

Q= I_вх *U_{вх*sin(Δφ}), где k=1,3,5

Коэффициент мощности:

Коэффициент искажений для :

Коэффициент искажений для: :

Коэффициент искажений для :

4.4 Эквивалентные синусоиды

Знак угла определяется знаком реактивной мощности цепи Q > 0 => .

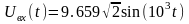
4. Расчет переходных процессов классическим методом.

4.1 Переходная и импульсная характеристика для входного тока и выходного напряжения

Рис.19. Схема четырехполюсника.

В качестве единичного входного воздействия выберем входное напряжение.

Исходные данные:

R₁ = 24 Ом;

R₂ = 40 Ом;

R₃ = 60 Ом;

L = 200 мГн.

Рис.20. Единичное входное воздействие.

Применим классический метод расчета. Характеристическое уравнение при заданных параметрах элементов схемы:

Рис.21. Характеристическая схема.

с^-1

с^-1

с

y(t) = Ae^-pt + y_вын

Рассмотрим момент времени t=0_-

Рис.22. t=0_-

u_вх(0_-)=0

i_вх(0_-) = i_L(0_-) = i₂(0_-) = 0

i_L(0_-) = 0

Рассмотрим момент времени t=∞

Рис.23. t=∞

u_вх(∞)=1 В

A

A

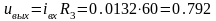B

Рассмотрим момент времени t=0₊

Рис.24. t=0₊

Так как ток в катушке не изменяется скачком, то

i_L(0_-) = i_L(0₊) = 0

Тогда i_вх(0₊) = i₂(0₊)

А = -0.008

B = -0.0032

C = -0.192

Переходные характеристики:

Импульсные характеристики:

Рис.25.

Рис.26.

Рис.27.

Рис.28.

Импульсная характеристика цепи является оригиналом передаточной функции

Переходная характеристика может быть определена через передаточную функцию с помощью обратного преобразования Лапласа:

Проверка:

Теорема о предельных соотношениях

1 )

2 )

Проверка выполнена.

4.2 Расчет входного тока и выходного напряжения

Из пункта 2.2 известно, что

В, А,

В.

=0 при t=0.

До коммутации на вход схемы подается напряжение , t=0-:

;

;

c.

После коммутации на схему подаются прямоугольные импульсы с амплитудой 10В.

Для интервала 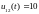В.

В момент t=0+ по закону коммутации имеем А.

В.

В установившемся режиме индуктивности замкнуты накоротко:

А.

В.

Зависимости имеют вид: .

В частности, .

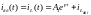найдем из условия =>

;

.

Значит, А.

Аналогично .

=>

;

.

Значит, В.

Для интервала В:

А;

В;

А;

В;

;

;

;

;

Значит, А.

Аналогично .

=>

;

;

Значит, В.

Рис.18. Графики входного тока и выходного напряжения для первого периода.

С использованием ЭВМ рассчитаем на интервале , где n – количество периодов, при котором наступает квазиустновившийся режим.

Рис.19. Графики входного тока и выходного напряжения для квазиустановившегося режима.