5. Схема Грина быстрых преобразований Уолша и Фурье.

Для матриц Сильвестра-Адамара имеет место следующая факторизация (разложение матрицы в произведение матриц)

,

где

J_k- единичная матрица порядкаk.

ДОКАЖЕМ указанную факторизацию индукцией по m.

При m=1 имеем

т.е. указанная факторизация справедлива.

Так как то можно записать, что

,

.

С учетом этих равенств имеем

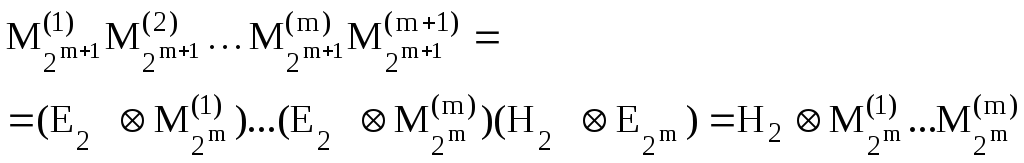
Так как по предположению индукции верно равенство , то

и факторизация доказана.

Например, при m =2 факторизация имеет вид

, где

,

.

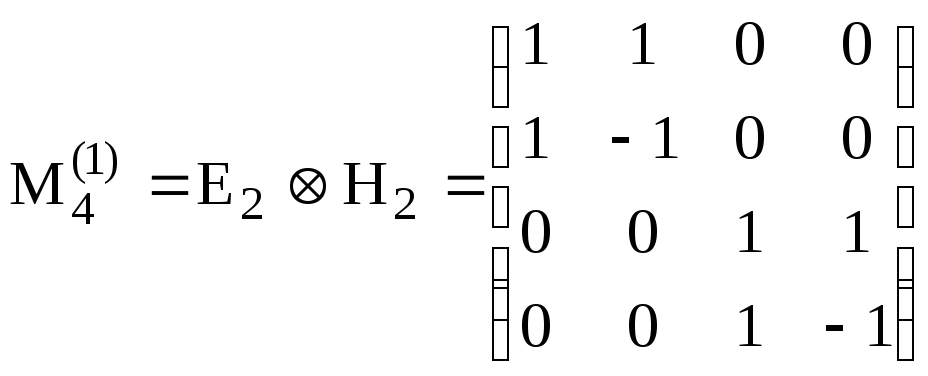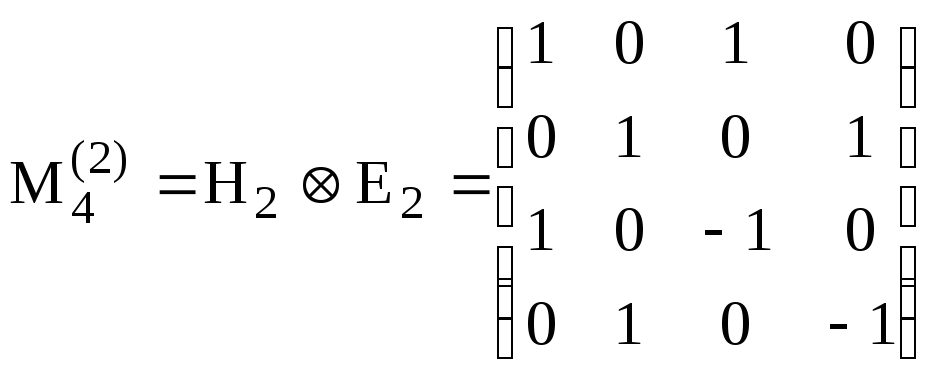Из равенств

следует, что матрица ,, содержит в каждой строке и в каждом столбце ровнодва ненулевых элемента, равных либо 1,либо -1.Следовательно, умножение любой вектор-строки размерности 2^mна столбец матрицысвязано с одной операцией сложения или вычитания компонент данной вектор-строки, а общее число таких операций при умножении вектора-строки на матрицуравно 2^m .Так как умножение вектора-строки на матрицуможно свести к последовательному умножению на матрицы ,то общее число операций при таком умножении равноm2^m. Отметим, что число умножений вектора-строки на матрицуHпорядка 2^mбез применения схемы быстрого, умножения требует 2^2mопераций. Способ быстрого умножения вектор-строки на матрицу Сильвестра-Адамара с использованием приведенной факторизации обычно называют схемой Грина. Применение этой схемы к равенствам (1)и (2)называют, соответственно, быстрым преобразованием Уолша-Адамара и быстрым преобразованием Фурье.

6. Критерий нелинейности булевых функций.

В соответствии с принципами, сформулированными К. Шенноном, при синтезе криптографических систем выдвигаются два требования, которые обычно называются требованием перемешивания и требованием рассеивания. Для обеспечения выполнения требования перемешивания для осуществления криптографических преобразований используются нелинейные функции. Таким образом, требование нелинейности для дискретных функций является весьма существенным для обеспечения криптографической стойкости шифрсистем.

В этой связи необходимо иметь критерий, определяющий меру нелинейности криптографических функций. Такой критерий должен учитывать известный в криптографии принцип, заключающийся в том, что функция является неприемлемой с криптографической точки зрения, если она простыми преобразованиями приводится к функции, не обладающей хорошими криптографическими качествами. Поэтому критерий нелинейности должен быть инвариантен относительно некоторой группы преобразований, переводящих одну функцию в другую.

Действительно, например, булева функция

содержит все нелинейные члены после перемножения. Однако, функция состоит из одного члена и является криптографически неприемлемой.

Как и ранее ниже для различения обозначений F – функция, а F₂ –конечное поле из двух элементов, для поля будем использовать обозначение GF(2), столь же общепринятое, как и F₂. Для множества всех двоичных наборов длины k (координатного векторного пространства над полем GF(2)) используем обозначение [GF(2)]^k.

Критерий нелинейности булевых функций.

В криптографических приложениях часто используются функции вида

.

Например, преобразования S-блоков шифрсистемы DES (см. параграф 1.4) определяются функцией

.

Вместе с тем, критерий нелинейности удобно сводить к критериям нелинейности булевых функций вида

.

В этих целях используется понятие линейной структуры. Говорят, что функция имеет линейную структуру, если существует такой ненулевой вектори нeтpивиaльнoe линейное отображениетакое, что сумма

принимает одно и то же значение, равное 0 или 1, для всех . Эта линейная структураможет быть выражена через линейные структуры булевой функции. По этой причине основное внимание будет уделено критериям нелинейности булевых функций f. В этих целях будет использоваться алгебраическая нормальная форма функции f , имеющая вид:

.

По определению считаем, что функция f нелинейна, если ее алгебраическая нормальная форма (многочлен Жегалкина) содержит члены степени выше первой.

Расстояние функции f до ближайшей аффинной функции L определим равенством

,

где - расстояние Хэмминга между f и L и A(n) - множество всех аффинных функций.

Для исследования - расстояния функции f до множества A(n) рассмотрим- группу всех обратимых преобразований пространства. В этой группе рассмотрим подгруппу AGL(n) всех аффинных преобразований. Известно, что любой элементможет быть записан в виде, где A – регулярная (невырожденная) матрицаи.

Положим

- множество всех булевых функций от nпеременных.

Действие группы на множествоопределим равенством

,

где .

В этих терминах описание критериев нелинейности функций можно сделать более общим и более точным. Любой такой критерий определяется функцией D

,

которая принимает значения из соответствующего множества W.

Функция f удовлетворяет критерию нелинейности, если D(f))W1, W1W - соответствующим образом определенное подмножество. Существенно, чтобы значения D были инвариантны при таких преобразованиях из, которые переводят функцию f в другую функцию g , не удовлетворяющую криптографическим требованиям. В совокупность таких преобразований обычно включают аффинные преобразования.

Для определения критерия рассмотрим максимальную подгруппу , которая оставляет D инвариантным, т.е.

.

Группу будем называть группой симметрий D. Исследование критериев нелинейности связано с описанием группы симметрий.

Прежде всего покажем, что расстояние до ближайшей аффинной функции инвариантно относительно операции действия аффинной группы. Этот результат получим в качестве следствия из теоремы, сформулированной ниже.

Пусть и дляобозначим;- группа всех обратимых преобразований.

Положим

=.

Будем называть группой симметрий множества H.

Теорема 1. Для любого подмножествагруппа симметрийсовпадает с группой симметрий H, т.е.

.

ДОКАЗАТЕЛЬСТВО состоит из двух пунктов.

а) Покажем, что . Возьмеми. Пустьтакое, что. Тогда, так как операция действияна Ф(n) оставляет инвариантным расстояние Хэмминга. Из определенияследует, чтои, следовательно,. Таким образом,при любом.

Так как есть подгруппа группы, то существует обратный элемент. Действуя этим элементом, получаем, что. Следовательно,и.

б) Покажем, что . Заметим, что для любогосуществует такое, чтои, следовательно,. С другой стороны, так как, то- получили противоречие..

Следствие 1.Группа симметрий J(для минимума расстоянийдо множества аффинных функций L есть аффинная группа.

С учетом теоремы 1 остается показать, что - аффинная группа.

Очевидно, что . Кроме того, для любогосуществует такой индекс i, что i -я компонента_i(x1,…,xn) вектораx не является аффинной. Тогда, если g(x1,…,xn)= xi, то функцияg(x1,…,xn)=_i(x1,…,xn). Отсюда следует, что