51. Определение частично рекурсивных функций. Основные функции.

52. Определение частично рекурсивных функций. Основные операции.

53. Определение частично рекурсивных функций.

54. Алгебраически неразрешимые проблемы.

55. Задачи Р- сложные. Полиномиально сложные задачи.

56.NP-проблемы. Экспоненциально сложные задачи.

57. СвязьNP-проблем с Р-проблемами.

МНОГОЗНАЧНЫЕ ФУНКЦИИ

Наряду с булевыми функциями в приложениях используются -значные функции и при > 2. Будем считать, что аргументы таких функций и сами они принимают значения из множества чисел

Определение 1. Функцией -значной логики, или -значной функцией, отnпеременных при n1 называется произвольное отображение

-значными функциями от 0 переменных называются функции-константы 0,1,..., -1.

Множества всех -значных функций и всех -значных функций отnпеременных обозначим соответственно через и .

При изучении -значных функций используются многие из терминов и обозначений, введенных при изучении булевых функций. В частности, сходным образом определяются равенство функций, существенные и несущественные переменные, функции от n переменных, тождественно равные константам 0, 1, ..., -1, подфункции и т. д.

Так как множество конечно, то -значную функцию от n переменных можно задать таблицей ее значений на всех наборах (или векторах) из . При этом условимся записывать их в порядке возрастания как чисел в А-ичной системе счисления. Непосредственно из табличного задания видно, что число различных -значных функций от n переменных равно . При >2 табличное задание -значных функций практически еще более трудно осуществимо, чем задание булевых функций. В связи с этим важным является вопрос о разработке аналитических способов задания -значных функций. При этом, как и в случае =2, естественно было бы воспользоваться какими-либо простейшими функциями и, в .частности, бинарными операциями на множестве .

Множество можно рассматривать как кольцо вычетов по

модулю , и потому можно считать определенными на операции сложения и умножения по модулю . Будем эти операции при >2 обозначать теми же значками • , + , что и операции над числами. Используя эти операции и функции-константы, можно построить кольцо многочленов от переменных . Каждый многочлен этого кольца представляет -значную функцию отnпеременных. Ниже будет доказано, что при простом , когда есть поле, многочленами представляются все -значные функции. При составном это не так. Действительно, если — собственный делитель числа , то все функции , представляемые многочленами, сохраняют отношение сравнимости по модулю :

.

Ясно, что не все -значные функции обладают этим свойством. Используя операции сложения и умножения, а также элементарные функции

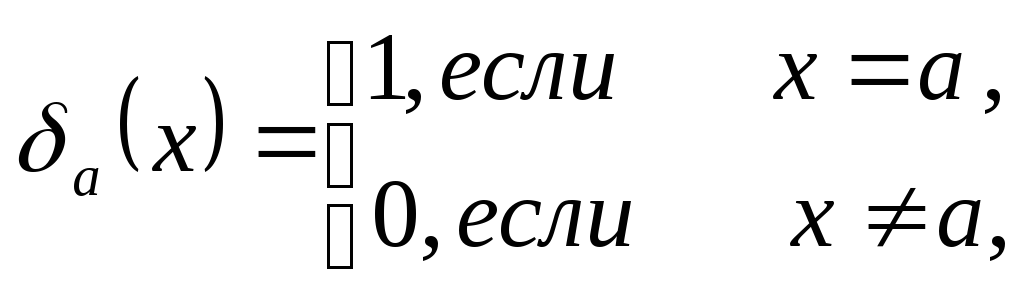
можно получить представление -значной функции, сходное с совершенной дизъюнктивной нормальной формой для случая =2.

(1)

Другими, часто используемыми операциями на являются аналоги дизъюнкции, конъюнкции и отрицания:

,

.

Для -значных функций, как и в двоичном случае, можно ввести понятия суперпозиции, представления функций формулами над заданной системой функций, замыкания, замкнутой и полной систем функций и т. д. Приведем примеры полных систем -значных функций.

1. Из представления (1) следует, что полной является система функций

.

2. Так как в разложении (1) операцию сложения можно заменить на дизъюнкцию (выбор максимума), то полной является также система функций

.

3. Наряду с разложением (1) имеет место еще один аналог совершенной дизъюнктивной нормальной формы функции

где

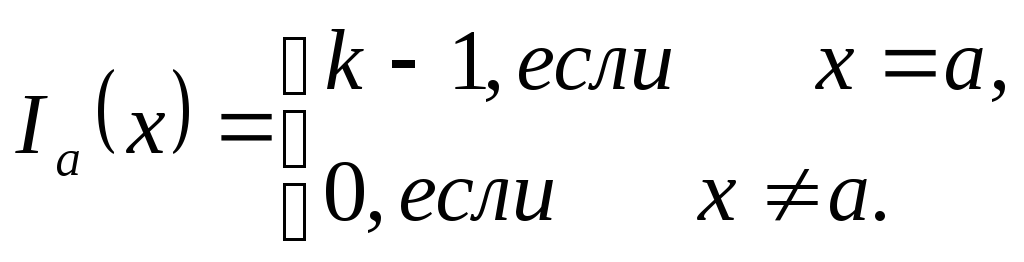
Отсюда следует, что полной является система функций

.

ФУНКЦИИ ШЕННОНА И ИХ ОЦЕНКИ.

Для описания сложности контактных схем К. Шенноном в работе [ 12 ] была введена числовая функция(n), равная такому наименьшему числу, что контактными схемами сложности не более(n) можно реализовать любую булеву функцию отnпеременных:

(n)=(f),

или более подробнее,

где минимум берется по всем контактным схемам S, реализующим функциюf.

Аналогичные функции можно ввести и для других типов схем, реализующих булевы функции, при различных определениях сложности схем. Все такие функции называют функциями Шеннона. Примерами функций Шеннона являются функции

для -схем и функции

=

для функциональных схем в любом фиксированном базисе.

В отмеченной выше работе [ 12 ] был указан подход к нахождению нижних оценок функций Шеннона и найдена нижняя оценка для (n) .точнее, была доказана

Теорема 1.Для любого >0 и больших n выполняется неравенство

Причем доля функций , для которых

Стремится к нулю с ростом n.

Для доказательства этой теоремы Шенноном была использована весьма простая идея, состоящая в следующем. Подсчитаем число N(n,k) не эквивалентных двухполюсных контактных схем сложностиреализующих функции от переменных и сравним его с числом.

Если окажется что N(n,k)>,то это будет означать, что не все двоичные функции от n переменных могут быть реализованы контактными схемами сложности, т.е. найдется хотя бы одна функциядля которой, а потому и подавно.

Более того эта идея отражена в следующем очевидном утверждении.

Лемма 1.Если для некоторой функцииk(n) с ростомn

, (1)

то,начиная с некоторого n,

,

причем доля функций , для которых

,

стремится к нулю.

Теперь мы оценим число N(n,k).

Лемма 2.

,

где с – некоторая константа, не зависящая от n.

Сначала заметим, что сложность контактной схемы – это число контактов в ней, или число ребер в соответствующем ей графе. Кроме того, если в схеме имеется изолированая вершина, отличная от полюса, то, отбросив ее, получим схему, реализующую ту же самую функцию. Поэтому число N(n,k) не превосходит числа неэквивалентных двухполюсных контактных схем, которые имеют не болееkребер, не содержат изолированых вершин,кроме может быть, полюсов, и реализуют двоичные функции от переменных.

Указанные схемы получаются из соответствующих графов с двумя фиксированными полюсами приписыванием к каждому ребру некоторой буквы . Поэтому сначала подсчитаем числонеизоморфных графов сhребрами, двумя фиксированными вершинами-полюсами и без изолированных вершин–не полюсов. Так как каждое ребро содержит две вершины, а изолированными вершинами могут быть лишь полюсы, то число вершин такого графа не превосходит 2h+2. Каждая вершина может соединяться с ребром с любой другой вершиной и с собой. Поэтому число различных пар вершин равно

.

Теперь из всех этих пар вершин нужно выбрать hпар, при этом следует учесть, что одна и та же пара может выбираться много раз, ибо две вершины в нашем графе могут соединяться несколькими различными ребрами. Отсюдане превосходит числа сочетаний с повторениями изrэлементов поh, т.е.

.

А так как (это следует из формулы Стирлинга), то

.

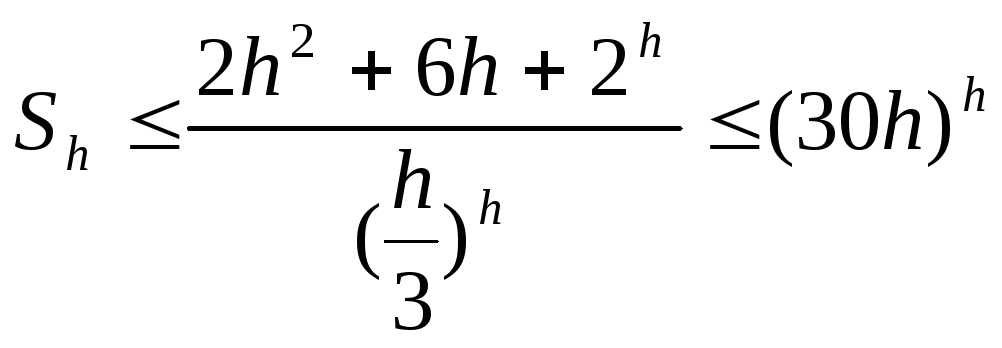Теперь нужно каждому ребру графа приписать один из 2nсимволов. Это можно сделать ровноспособами.

В итоге получим контактных схем сложностиh. Теперь осталось просуммировать поhот 0 доk:

.

Теперь для доказательства теоремы Шеннона достаточно показать, что при ивыполнено условие (1). Действительно, из (2) следует, что

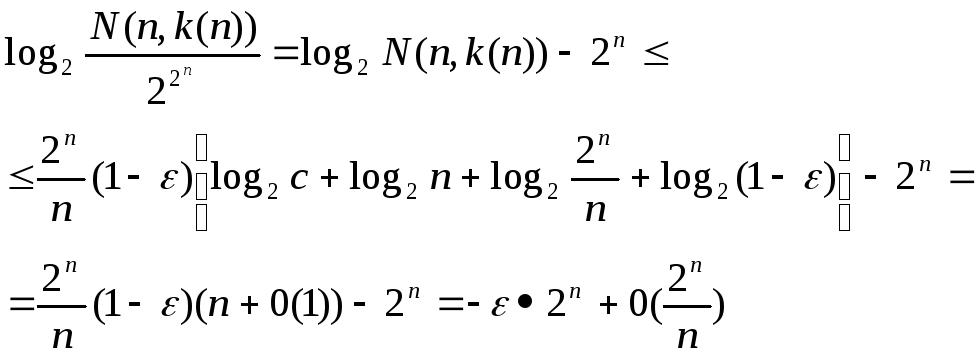
Отсюда видно, что

а поэтому

этим теорема шеннона доказана.

Верхние оценки для функции получается сложнее, поскольку для их получения необходимо уметь эффективно строить контактные схемы в заданных пределах сложности для реализации всех булевых функций из.

Отметим без доказательства относящийся сюда результат Шеннона:

Для любого , найдется такое, что для

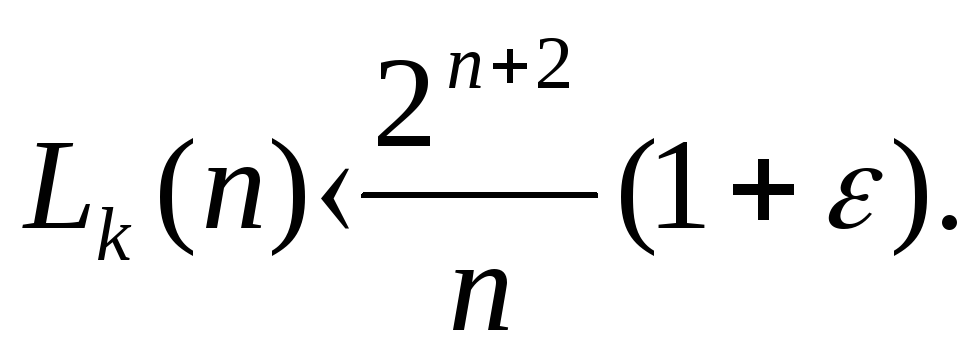
этот результат в 1958 году был улучшен Лупановым О.Б., который создав оригинальные и достаточно тонкие методы синтеза схем, доказал (см. 10), что для любого и

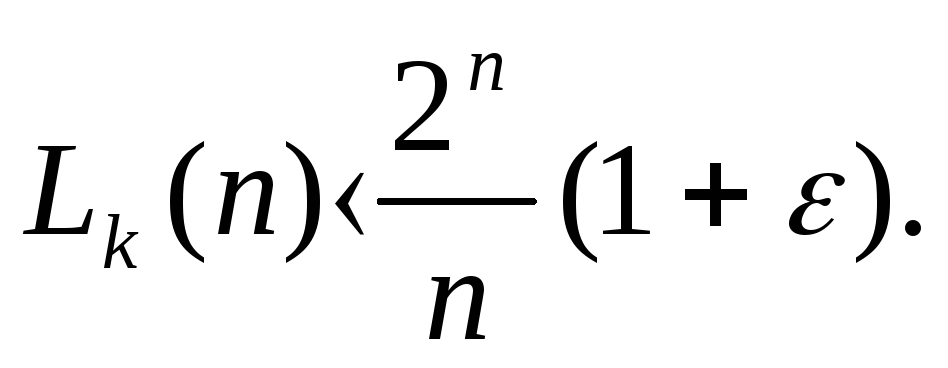
отсюда и из доказанной выше теоремы Шеннона вытекает асимптотическое равенство

(2)

итак, из всего сказанного видно, что при достаточно больших n почти все двоичные функции от n переменных имеют максимальную сложность в классе контактных схем, порядок которой совпадает

в конце 50-х годов О.Б Лупановым были доказаны также асимтотические равенства

(3)

для сложности схем и

(4)

для сложности функциональных схем в базисе

Подробное и доступное изложение доказательств соотношений (2). (3), (4) содержится в работе [10]. Для доказательства каждого из этих соотношений автор находит асимптотические совпадающие нижние и верхние оценки для соответствующих функций. Нижние оценки находятся изложенными в доказательстве теоремы 1 методом Шеннона. Верхние- путем синтеза соответствующих схем. Мы проиллюстрируем его в наиболее простом случае, на отыскании оценки сложности функциональных схем в базисе (см. [10], [5]).

Теорема 2. Приимеет место асимптотическое неравенство

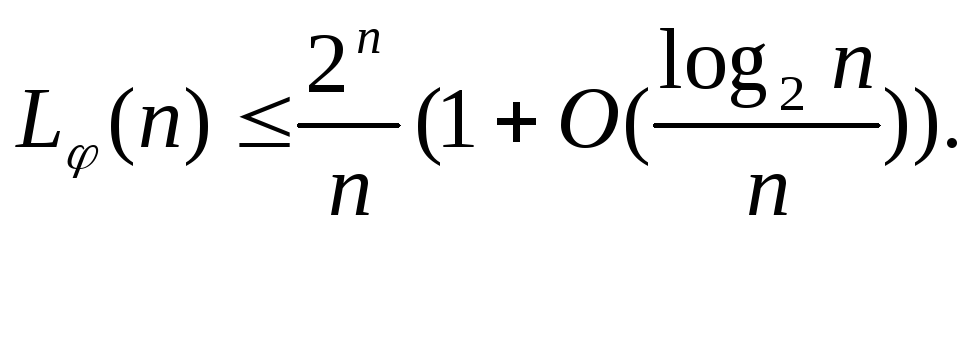
Доказательство. Пустьлюбая булева функция. Разобьем множество переменныхна подмножестваи, где k- пока произвольный параметр,и зададим функциютаблицей 14.

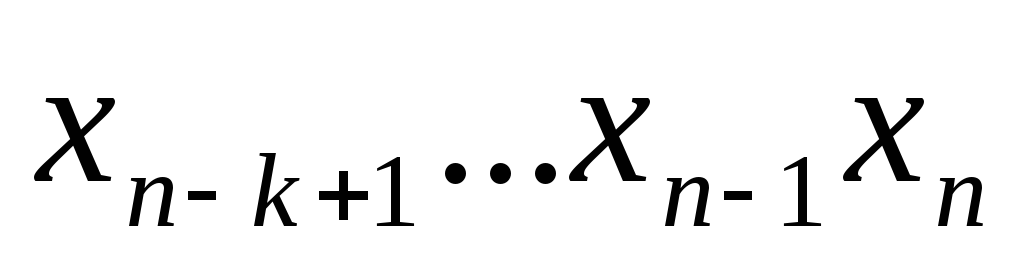
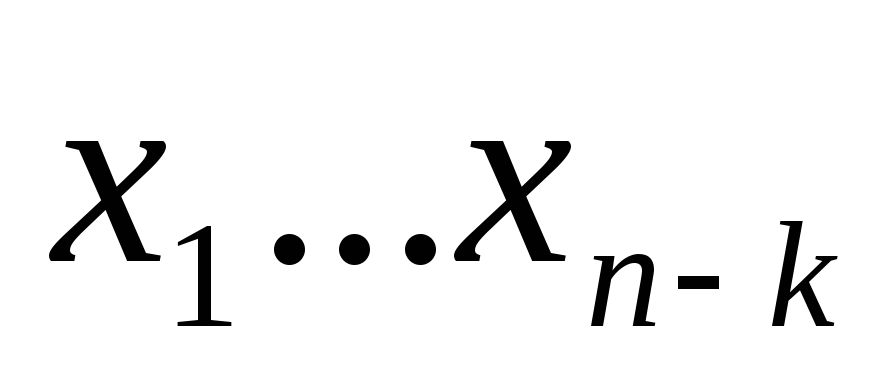
		0 0 … 1 . . … . . . … . 0 1 … .
0 … 0 0 0 … 0 1 …………………………………… …………………………………… 1… 1 1
	…	…

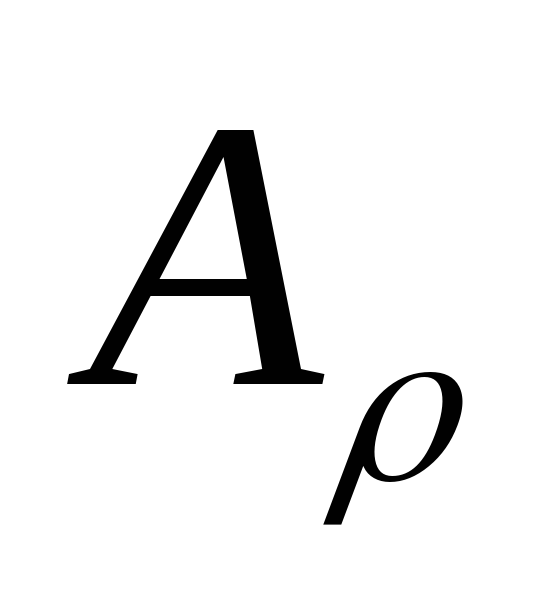
Разобьем строки матрицы значение функциина полосыпострок в каждой полосе, кроме последней, в которой может оказаться

Обозначим через функцию, значения которой совпадают в полосесо значениями функциии равны нулю во всех остальных случаях. Еслистолбец значений функцийв полосе, то обозначим через,функцию, матрица значений,которой получается иззаменой в полосевсех столбцов, отличных отнулевыми столбцами. Представим функциюв виде произведений функцийизависящих соответствующих от переменныхиМатрицаполучается заменой встолбцов полосы, равных, столбцами из единиц, а-заменой в полосематрицывсех столбцов столбцами.

Очевидно равенство.

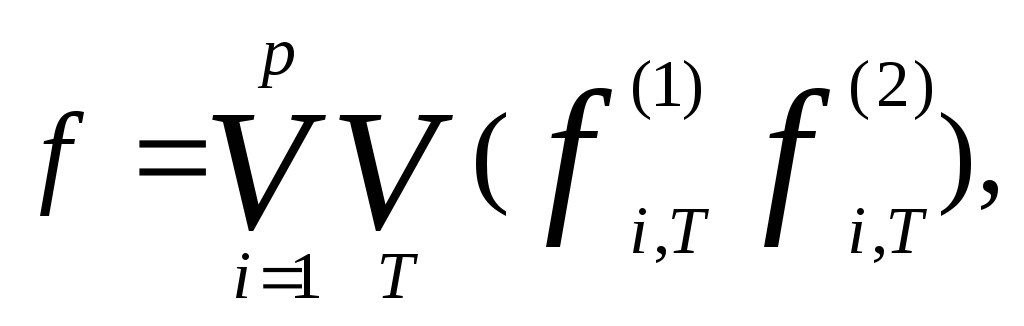
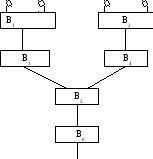
называемое 1-м представлением функции f. Пользуясь представлением (5), построим функциональную схему, реализующую функциюf. Схема будет состоять из 6 блоков (см. рис. 22).

f

Рис. 22

Блок В₁реализует систему всех конъюнкций вида

и содержит n-kэлементов-отрицаний и не болееn-k-1 элементов-конъюнкций. Следовательно, его сложность

Блок В₂ реализует систему всех конъюнкций вида

и потому

Блок В₃реализует все нулевые функцииисходя из конъюнкций (6). Очевидно, что при фиксированномiкаждая конъюнкция вида (6) используется только в одной из функцийОтсюда следует, что

Блок В₄реализует все функции видаисходя из конъюнкций (7).Так какесть дизъюнкция не болееsконъюнкций вида (7) при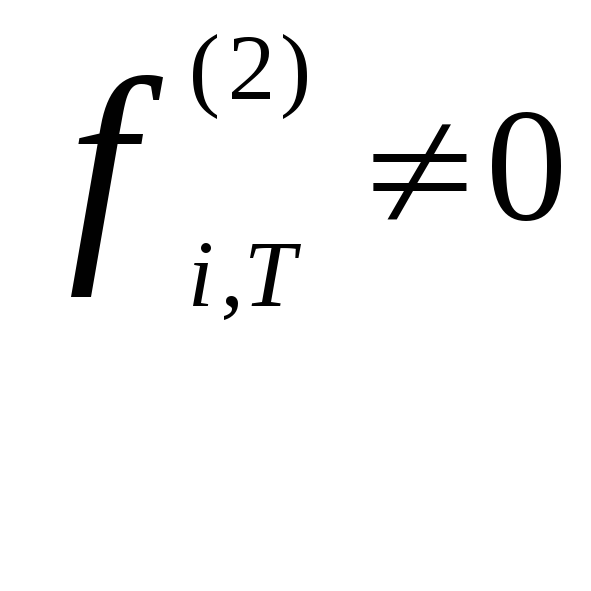и двух конъюнкций прито

Блок В₅ реализует произведения

и потому

Блок В6 реализует fкак бы дизъюнкцию функцийи

В итоге имеем:

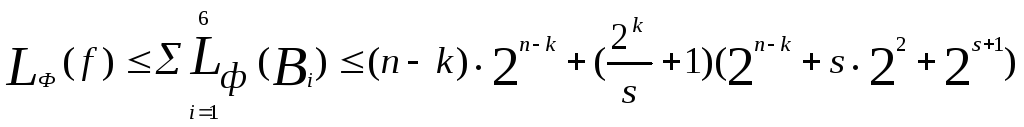
Теперь требуется минимизировать полученную оценку как бы функцию от параметров kиs. Мы опустим все рассуждения, связанные с обоснованием их выбора, а сразу положим:

(логарифм двоичный). Тогда имеем:

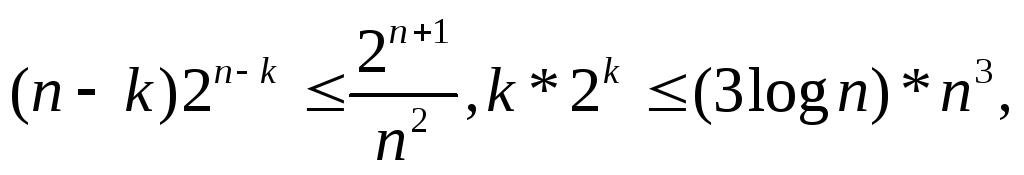
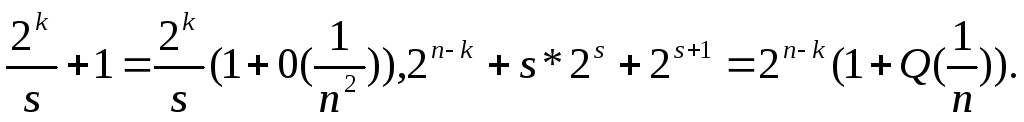
отсюда и следует,что

А так как полученная оценка верна для любой функции то теорема доказана.

В литературе рядом авторов, в том числе и О.Б. Лупановым, рассматривалась функция Шеннона L(n) и для функциональных схем в произвольном конечном базисе. Оказалось, что для любого конечного базиса существует такая константаC, что

В связи с этим интересно отметить, что для функции Шеннона E(n) види-положительная константа, зависящая только от базиса (см.[9]). В этой же работе рассмотрен вопрос об одновременной минимизации функцийL(f) иE(f).

Параграф 6. 7. Математические основы синтеза булевых функций с гарантированными криптографическими свойствами.

Введение. При написании данного параграфа использована начальная часть работы В.Н. Сачкова, В.И. Солодовникова, М.В. Федюкина «Дискретные функции, используемые в криптографи», М., 1998 г., любезно предоставленная ими авторам данной книги. Здесь рассматриваются основные свойства матриц Сильвестра-Адамара, с использованием которых вводятся преобразования Уолша-Адамара и Фурье булевых функций. Приводится схема Грина быстрых преобразований Уолша-Адамара и Фурье. Определяются критерии нелинейности булевых функций, инвариантные относительно групп преобразований переменных, являющихся подгруппами группы всех аффинных преобразований. Вводятся понятие линейной структуры булевой функции и понятие расстояние булевой функции до множества функций, имеющих линейные структуры. Определяется порядок нелинейности булевой функции являющейся одним из критериев нелинейности булевой функции. Булева функция, имеющая максимальное расстояние до линейных структур, называется совершенной нелинейной функцией. Оказывается, что эти функции находятся также на максимальном расстоянии и от аффинных функций. Класс совершенно нелинейных функций совпадает с классом так называемых «бент-функций», у которых модуль преобразования Уолша-Адамара, принимает единственное значение.