
- •Алгоритмы и сложность вычислений. Введение
- •49. Определение нормальных алгоритмов Маркова.
- •§ 1. Нормальные алгоритмы
- •50. Определение Машины Тьюринга.
- •§ 2. Машины тьюринга
- •51. Определение частично рекурсивных функций. Основные функции.
- •1. Матрицы Адамара и их свойства.
- •2. Матрицы Силъвестра-Адамара их свойства.
- •3. Преобразования Уолша-Адамара булевых функций.
- •4. Преобразование Фурье булевой функции.
- •5. Схема Грина быстрых преобразований Уолша и Фурье.
- •6. Критерий нелинейности булевых функций.
- •7. Расстояние до линейных структур.
- •8. Порядок нелинейности.
- •9. Совершенно нелинейные функции.
- •10. Расстояние до аффинных функций и корреляция.
- •11. Булевы функции от нечетного числа аргументов.
4. Преобразование Фурье булевой функции.
Для булевой функции f(V), имеющей таблицу истинности f=(f(V0),…,f(V2m-1)), где векторы V0,…,V2m-1расположены в порядке возрастания чисел, для которых они являются двоичными разложениями, преобразование Фурье определяется как вектор
Cf=(Cf(U0), Cf(U1),… Cf(U2m-1)),
где {U0, U1,…, U2m-1} совокупность всех двоичных векторов, а координаты Cf(U) определяются равенством
![]() где,
как и ранее, скалярное произведение
(U,V) вычисляется по модулю 2.
где,
как и ранее, скалярное произведение
(U,V) вычисляется по модулю 2.
Числа Cf(U) называются коэффициентами Фурье булевой функции f.
Из последнего равенства следует, что
![]() ,
(2)
,
(2)
где H - матрица Сильвестра-Адамара порядка 2m. А так как из соотношения (2) следует, что
![]() то
для коэффициентов Фурье получаем
следующую формулу
то
для коэффициентов Фурье получаем
следующую формулу
![]()
Рассмотрим некоторые свойства коэффициентов Фурье булевой функции.
10.![]() ,
,
где
Cf(0) - значение коэффициента Фурье
булевой функции f для нулевого вектора,
a![]() вес булевой функции f, т.е. число таких
значений
вес булевой функции f, т.е. число таких
значений![]() ,
для которых f(V)=1.
,
для которых f(V)=1.
Из свойства 1° следует, что булева функция f является cбалансирован-ной (равновероятной)тогда и только тогда, когда для нулевого коэффициента Фурье имеет место равенство
![]() .
.
2°.
Для любого вектора ![]() имеет
место равенство
имеет
место равенство
![]() .
.
3°.
Для любого вектора
![]() имеет место соотношение
имеет место соотношение
![]() ,
,
где
P(f(V)=(U,V)) — вероятность совпадения
значений булевой функции с линейной
функцией (U,V) при случайном равновероятном
выборе вектора
![]() ,
скалярное произведение (U,V) вычисляется
по модулю 2.
,
скалярное произведение (U,V) вычисляется
по модулю 2.
ДОКАЖЕМ 3°. Действительно, имеем
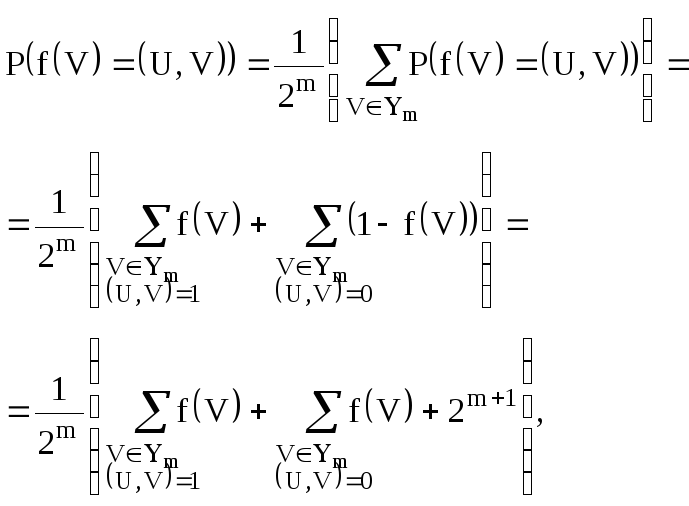
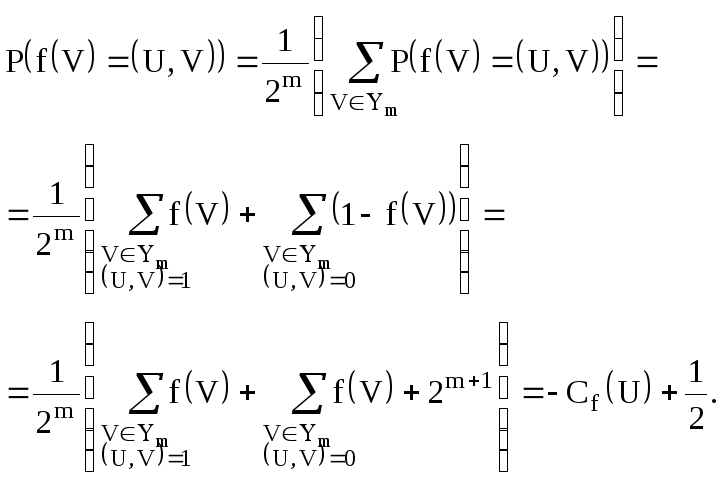
Таким образом,
![]() .
.
Отсюда вытекает требуемое равенство из свойства 3° .
В криптографических исследованиях иногда используют вектор
![]() координаты
которого связаны с коэффициентами
Фурье равенством
координаты
которого связаны с коэффициентами
Фурье равенством
![]()
Вектор
![]() называется статистистической структурой
булевой функции,а его координаты
называется статистистической структурой
булевой функции,а его координаты![]() - коэффициентами статистической
cтруктуры этой функции. Для U=0 обычно
полагают
- коэффициентами статистической
cтруктуры этой функции. Для U=0 обычно
полагают
![]() .
.
4°. Для коэффициентов Фурье булевой функции имеет место соотношение
![]()
ДОКАЖЕМ это равенство, действительно, из равенства (2) следует, что
![]() .
.
Из доказанного сейчас равенства для коэффициентов статистической структуры вытекает равенство Парсеваля
![]() .
.
Из
формул
![]() и
и![]() для коэффициентов Фурье булевой
функции получаем, что для
для коэффициентов Фурье булевой
функции получаем, что для![]()
![]()
Из
равенств
![]() и
и![]() следует, что
следует, что
![]()
Для коэффициентов статистической структуры имеют место неравенства
![]()
Оценка
сверху для
![]() следует из равенства
следует из равенства ![]() .
Оценка снизу вытекает из равенства
Парсеваля . Действительно,
допустим, что
.
Оценка снизу вытекает из равенства
Парсеваля . Действительно,
допустим, что
![]() .Тогда
.Тогда
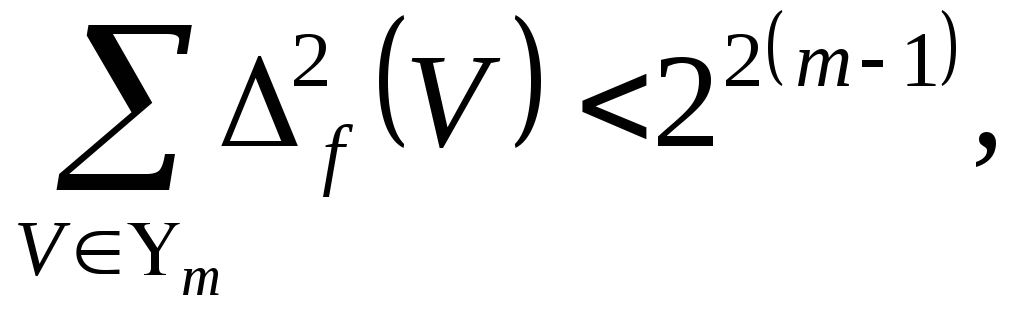
что противоречит равенству Парсеваля.
