1. Матрицы Адамара и их свойства.

Определение. Матрица H=(h_ij), i,j{1,2,…,n} такая, что h_ij{1,-1}, называется матрицей Адамара, если имеет место равентво

HH^T=nЕ ,

где H^T- транспонированная матрица H и Е — единичная матрица.

Матрица Адамара обладает следующими свойствами.

1. .

2. HH^T = H^TH .

Имеем HH^T = H^-1HH^TH=nЕ.

3. Если H₁,…,H_n - строки, H⁽¹⁾,…,H⁽ⁿ⁾ – столбцы матрицы H, (H_i,H_j) и (H⁽ⁱ⁾,H^(j)) – скалярные произведения соответствующих векторов, то

.

4 .

Отметим, что каждое из четырех условий при h_ij=является характеристическим, т.е. определяет все остальные свойства и, стало быть, определяет матрицу Адамара.

4. Перестановка строк или столбцов, умножение на -1 строк или столбцов переводят матрицу Адамара снова в матрицу Адамара.

5. Для существования матрицы Адамара порядка n, необходимо, чтобы либо n = 1,2 , либо n0(mod 4).

При n=1 и n=2 матрицы Адамара существуют и имеют вид

с точностью до перестановки строк, столбцов и умножения их на –1.

Используя свойство 4 любую матрицу Адамара порядка n можно привести к нормализованному виду, при котором матрица Адамара имеет первую строку и первый столбец, состоящие только из единиц. Рассмотрим первые три строки матрицы Адамара , приведенной к нормализованному виду. Соответствующая подматрица 3n матрицы имеет столбцы вида

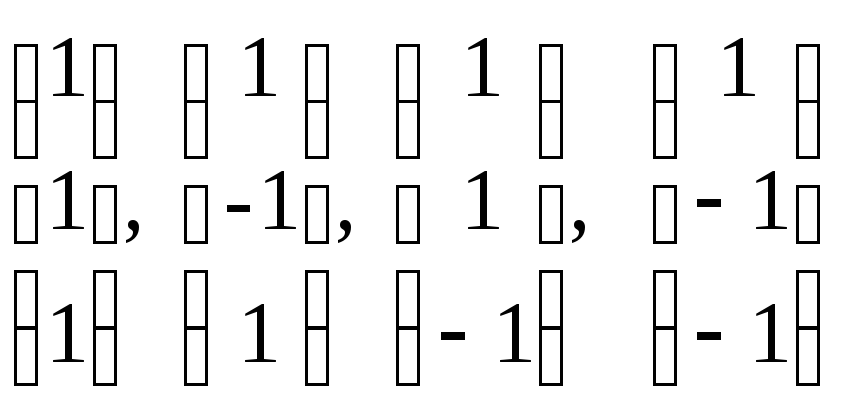
x,y,z, Если число таких столбцов в подматрице 3n равно соответственно w, то имеют место следующие соотношения

x+y+z+w=n

x+z=y+w

x+y=z+w

x+w=y+z .

Первое равенство означает, что общее число столбцов равно n. Последующие равенства следуют из ортогональности 1 и 2 строк, 1 и 3 строк, 2 и 3 строк подматрицы 3n. Нетрудно убедиться (например, приведением матрицы системы к треугольному виду методом Гаусса), что детерминант приведенной системы линейных уравнений относительно неизвестных x, y, z, w отличен от нуля и, стало быть, эта система имеет единственное решение: x=y=z=w=n/4. Следовательно, n0(mod 4).

Кронекеровское произведение матриц A=(aij), i,j=1,2,…,n; B=(bij), i,j=1,2,…,m определяется равенством

.

6. Если Hm и Hn — матрицы Адамара, то их кронекеровское произведение - снова матрица Адамара.

Из свойств кронекеровского произведения следует, что элементы матрицы равны ± 1. Кроме того,

где Еm - единичная матрица порядка m.

2. Матрицы Силъвестра-Адамара их свойства.

Матрицы Сильвестра-Адамара имеют порядок n, где n=2k, k=1, 2,…, n и определяются рекурретным соотношением

k=1, 2,… ,

где

.

Матрица Сильвестра-Адамара обладает свойством симметричности, а именно

,

что следует из ее определения.

Независимо от свойства 6 можно убедиться, что матрица H2k действительно является матрицей Адамара. Доказательство можно провести индукцией по к. Имеем: Н2- матрица Адамара ,

.

В силу равенства

для обратной матрицы имеем выражение

.

Рассмотрим совокупность всех двоичных m -мерных векторов V0, V1,…, V2m-1, координаты которых принимают значения 0 или 1. Будем предполагать, что эти векторы расположены в порядке возрастания чисел, для которых они являются двоичными представлениями. Для векторов Vi=(Vi(1),…,Vi(m)), Vj=(Vj(1),…,Vj(m)) будем рассматривать их скалярные произведения

,

где сложение ведется по модулю 2. Покажем, что матрица

есть матрица Силъвестра-Адамара. Доказательство проведем индукцией по m. При m=1 утверждение верно, так как матрица H₂имеет вид

.

Введем обозначения

.

Матрицу H₂^m+1представим в виде

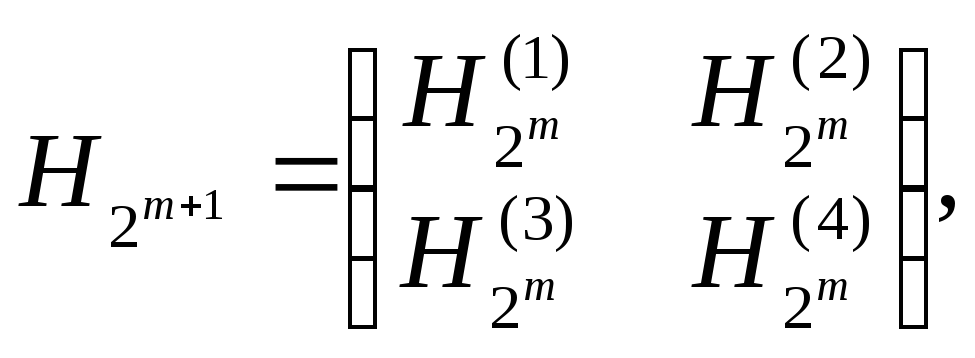
где

, , ,

где (0,0), (0,1), (1,0), (1,1) - скалярные произведения векторов размерности единица, . Очевидно, что

,

где - матрица Сильвестра-Адамара порядка 2^m . Следовательно,

и - матрица Сильвестра-Адамара порядка 2^m+1 .