Лекции / 2-й семестр / ЛЕКЦИИ~3

Доказательство: эти многочлены попарно взаимно простые  НL(F) – однозначно представляется в виде: H=V₁+V₂+…+V_r; V_jL(, а для семейства L( - базис по теореме : соберём базисы всех V_j  последовательности - базис pL(F)

Ч.Т.Д.

Пример: F(x)=(x-1)²(x-3); GF(5);

пусть начальный вектор: (001); U(1999) - ?

Решение: L(x-1)², L(x-3) 

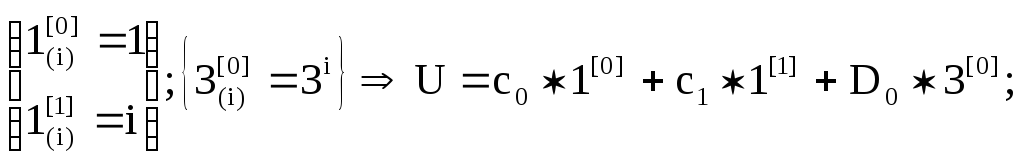
U(i)=c₀+c₁i+D₀3ⁱ; c₀,c₁,D₀ - ?

Начальный вектор:;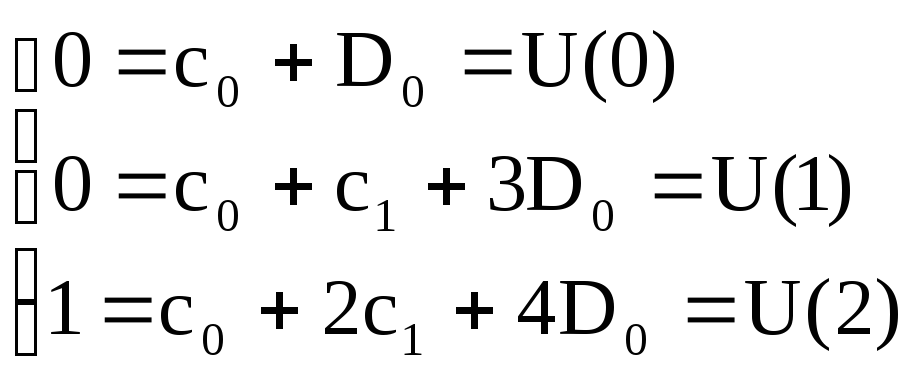

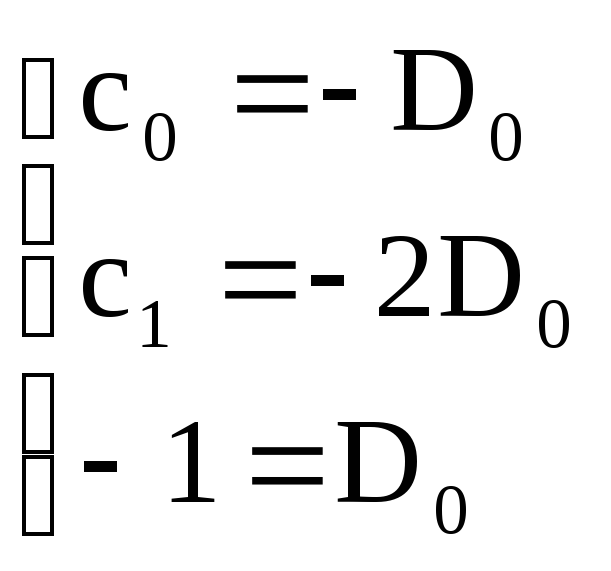
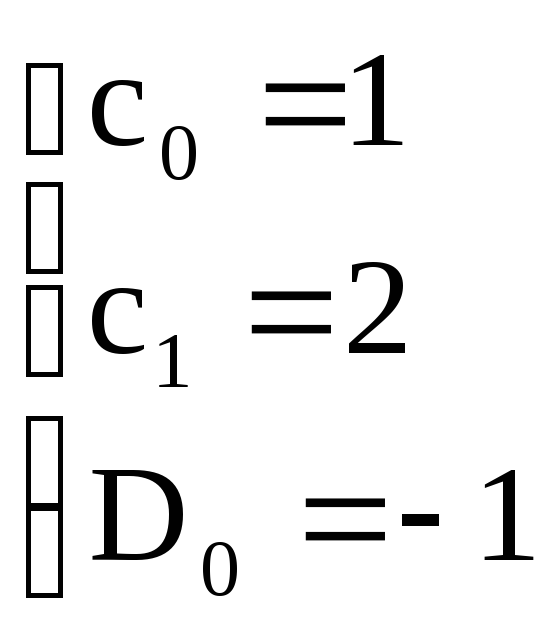U(1999)=1+21999-3¹⁹⁹⁹=1+29-3¹⁹⁹⁹=4-3¹⁹⁹⁹=4-2=2;

Ответ: U(1999)=2.

Представление ЛРП через функцию “след”.

Теорема: пусть РGF(q); f(x) – неприводим над Р, degf(x)=m   - корень f(x) в Q=GF(q^m) 

 UpL(f),  aQ:

Доказательство: 1. Покажем, что последовательность: ;

f(x)V=W; 

VpL(f);

А последовательностей вида V_i= число различных аQ=q^m;

 А последовательностей pL(f)=q^m – тоже.

Осталось показать, что все последовательности V_i - попарно различны:

пусть есть совпадающие последовательности:

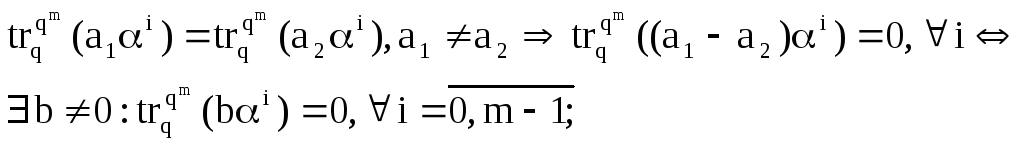
пусть с_jP:

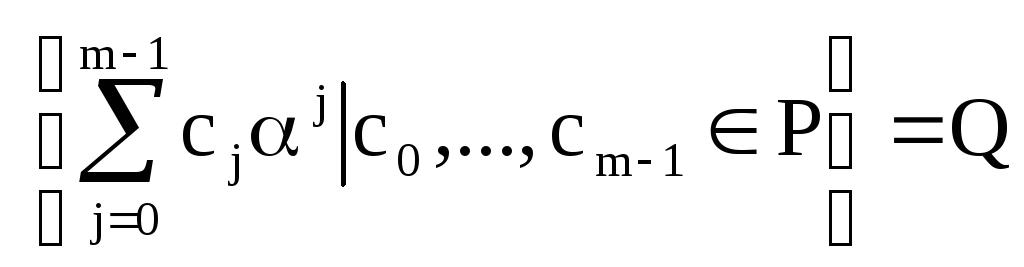- более большое поле, чем Р.

Лемма: число решений этого уравнения: q^m-1;

Доказательство:

  с – число решений исходного уравнения (число корней многочлена

1. пусть N_c – число корней

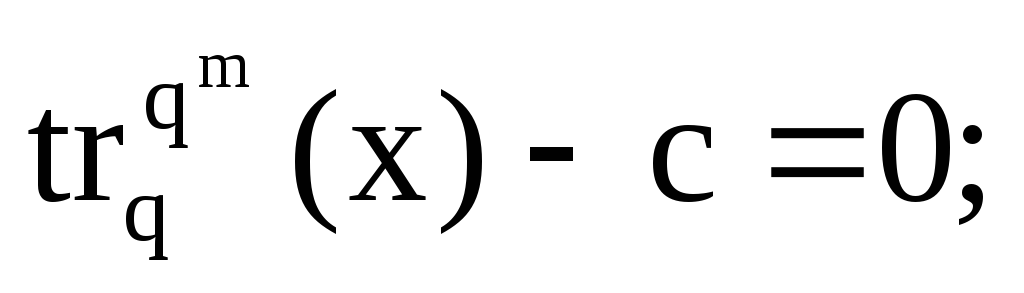
2.  xQ,

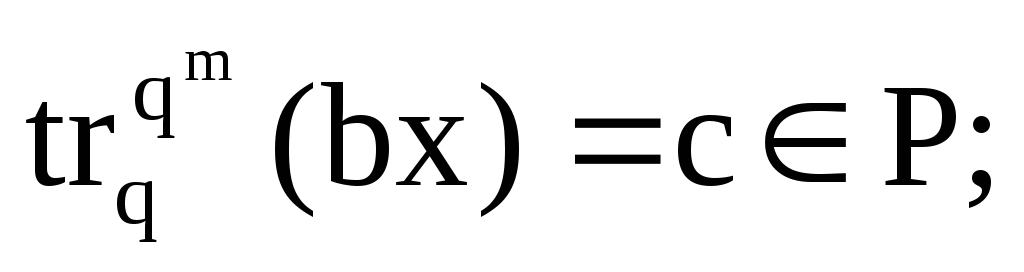
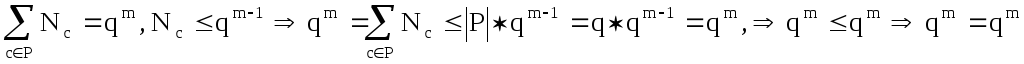3. , а это при N_c=q^m-1; q^m-1q^m – противоречие;

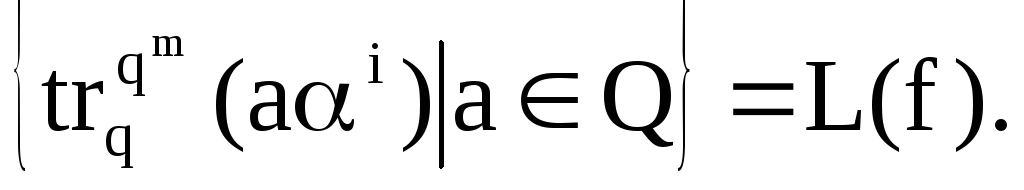
Ч.Т.Д.

Теорема: обозначим последовательности V_s: 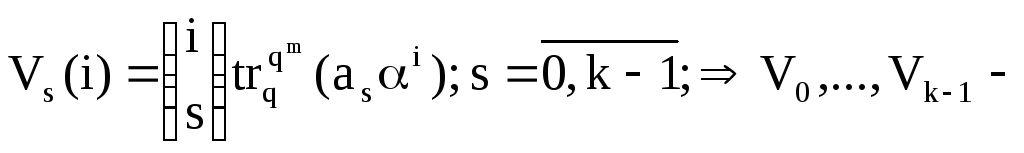базис

Доказательство:

;

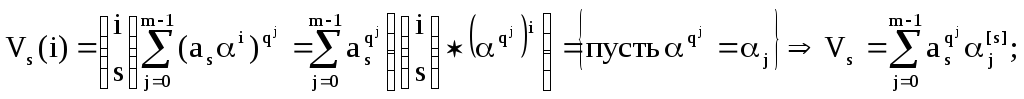
то есть все последовательности . Осталось показать, что все V_i различны и их число =(q^m)^k:

1. ;

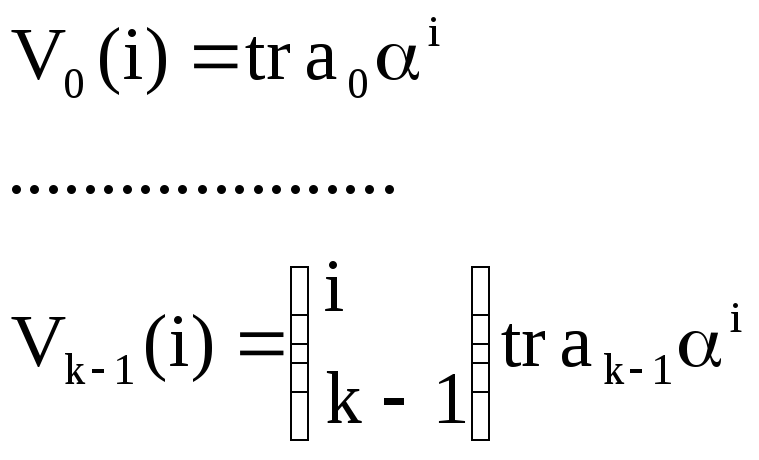Число сумм этих последовательностей – сколько наборов (а₀…а_k-1), а их (q^m)^k;

2. Осталось, что все 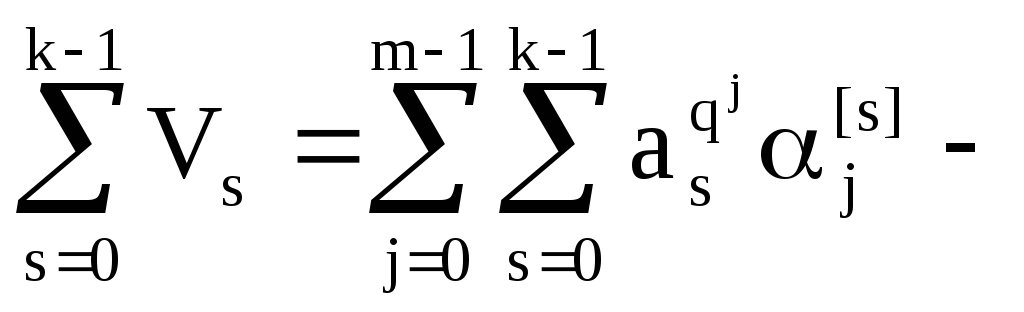попарно различные, а биномиальные последовательности 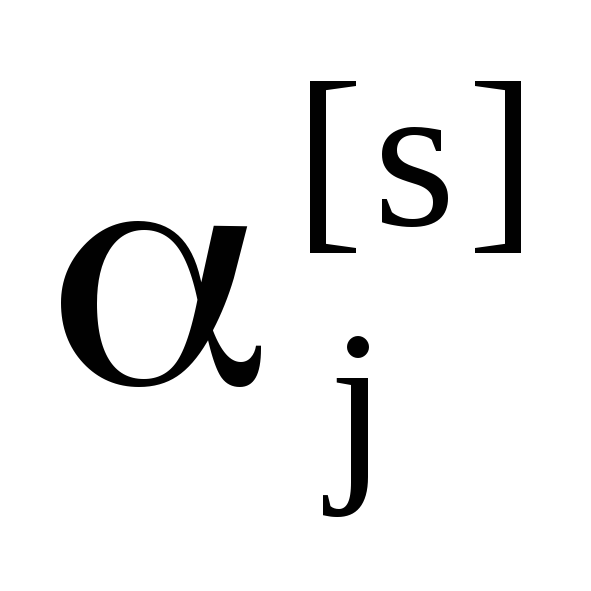базисные  не может быть совпадающих сумм, иначе это не базис  все суммы попарно различные  других последовательностей в L(f(x)^k), кроме вида V_i нет.

Пример: f(x)=x²+x+1; GF(2);

в GF(4) Q: Q²=Q+1;

U(i)=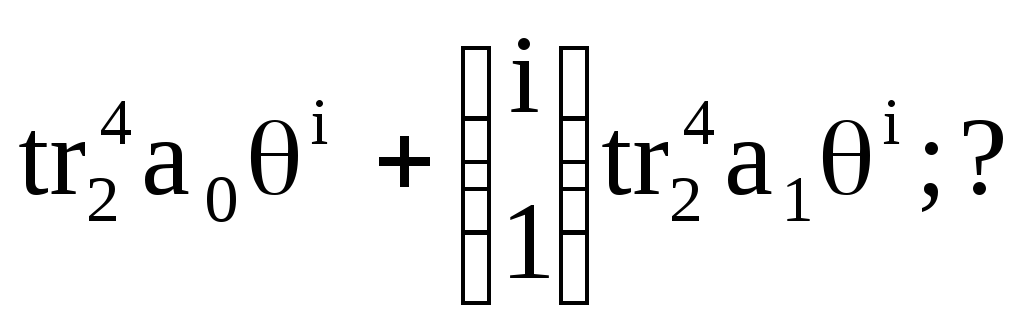

Опредление1: U^- периодическая последовательность если  ₀б, t:  i:

U(i+t)=U(i); (1)

пусть R;

Утверждение: если R то  U и U – периодической  U-ЛРП.

Определение2: если U^ ,U – периодическая, то наименьшее t, для которого  ₀ и выполняется (1) – период U; - T(U).

При этом наименьшее :  i>: U(i+T(U))=U(i) (3) – длина подхода U - (U) (l предпериода).

Теорема1: если U периодическая и ^, то любые числа  и t, удовлетворяют (1)  (U) и T(U)t; (4)

Доказательство: пусть множество M,M(U)+T(U);

Пусть Р – поле, РM;

  - инъективное отображение: , так строим

₀,t x^(x^t-e)=(0); (5)

то есть (2) выполняется для когда - периодическая  x^(U)(x^T(U)-e)=(0) 

(4) (5) x^{ (U)}(x^T(U)-e) x^(x^t-e)(5)

(5)(4) (A(x), B(x))= x^l(x^t-e, x^T(U)-e); tT(U);

x^t-e=x^t-T(x^T-e)+(x^t-T-e).

Примечание: (x,(x-e))=1;

(x^t-e;x^T-e)=(x^t-T-e,x^T-e); t+Tk;

x^l(x^d-e)=(0); dT, dT  d=T.

Следствие1: если U- периодическая, то (U)- наименьший >0, ₀ для которого  t.

Теорема2: если U- периодическая последовательность над кольцом R, то  H(x)R[x], V=H(x)U – тоже периодическая, и

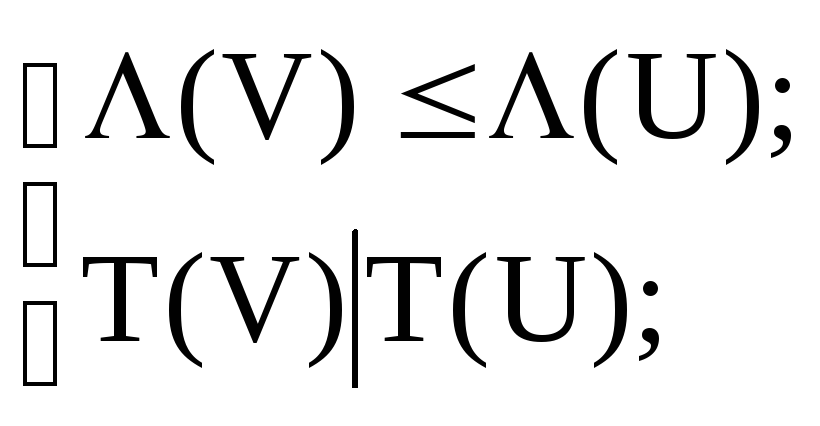
Доказательство: пусть (U)₀, T(U)T₀;

Ч.Т.Д.

Теорема3: пусть U,VR^- периодические  W=U+V и ;

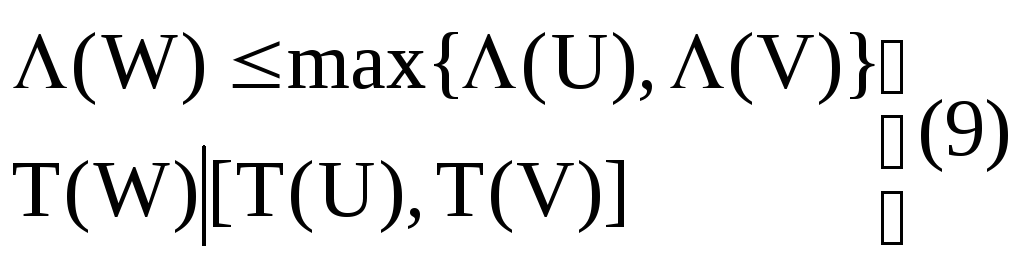1. (U) (V)  (W)=max{(U), (V)}; (10)

2. (T(U), T(V))=1  T(W)=[T(U), T(V)];

Доказательство: 1) =max{(U), (V)}; t=[T(U), T(V)];

x^(x^t-e)U=(0)

x^(x^t-e)V=(0)  x^(x^t-e)W=(0)

1. пусть (U)< (V)  =(V) и пусть (W)<; x^(x^t-e)U=(0) и x^-1(x^t-e)(W-U)=(0)

(V)-1- противоречие  предположение ошибочно.

2. пусть (T(U),T(V))=1, T(W)= тогда можно записать: [,T(U)]=k  так как k, то T(U)k  применяя Т1:

x^(x^k-e)W=(0)

x^(x^k-e)U=(0)  x^(x^k-e)V=(0)  T(V)k.

Определение3: периодическая последовательность U над R^ -чисто периодическая если её предпериод =0 ((U)=0).

Определение4: периодическая последовательность U над R – вырожденная, если она имеет вид:

U=(U(0), U(1), …, U(-1), 0, 0, 0, …..).

Теорема4: любая периодическая последовательность UR^: U=U₀+U₁; (12)

, где U₀- вырожденная и U₁- чисто периодическая последовательность, при этом

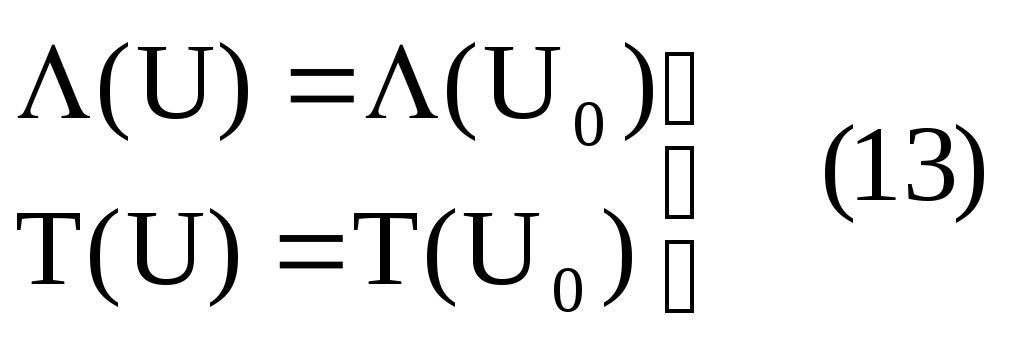
Доказательство: 1) обозначим (U)=, T(U)=t  UL_R(x^(x^t-e));

2. (x, x^t-e)=e  (x^, x^t-e)=1;

L_R(x^(x^t-e))= L_R(x^)+ L_R(x^t-e)  разложение верно и единственно, U₀-выбирается из L_R(x^)

U₁ выбирается из L_R(x^t-e);

Пример: U=() Z₄!

(U)=5;

T(U)=4; U=U₀+U₁

Решение: k; tk;

x^tkU=x^tk(U₀+U₁)=x^tkU₁=U₁;

x^tkU₀=(0);

x⁸U=(031203120..);

U₀=U-U₁=(01101000..).

Определение5: многочлен F(x)R[x] – периодический многочлен, если  ₀₀, tN: F(x)x^(x^t-e) (15).

T(F)- период многочлена F(x);

Наименьшее : F(x)x^(x^t-e)- обозначим через (F)- предпериод многочлена.

Теорема5: a) пусть унитарный многочлен F(x)R[x]; F- периодический  ЛРП е^F_RL(F);

e- (соот. ЛРП) тоже периодическая.

b) F- периодический многочлен  (F)=(е^F);T(F)=T(e);

 ЛРП U_RL(F), (U)(F); T(U)T(F);

Доказательство: a) A_nn(е^F)=R[x]F(x);

 ₀,  tN: x^(x^t-e)е^F=(0)  F(x)x^(x^t-e);

b) U_RL(F), F(x)U=(0); F(x)x^(F)(x^T(F)-e); x^(F)(x^T(F)-e)U=(0);

Следствие1: если F(x)R[x], то ₀, tN: F(x)x^(x^t-e)  (F), T(F)t;

Следствие2: если F(x), G(x)R[x], (F(x), G(x))e, то H(x)=F(x)G(x),

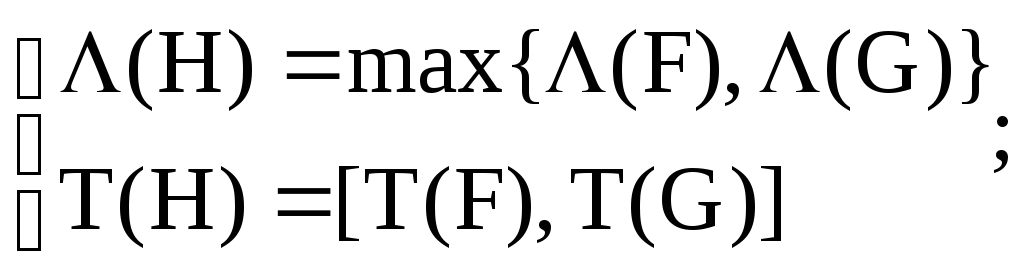
Лекция.

Определение1: UR^- периодическая, если 0, t>0: U(i++t)=U(i+), i0. (1)

Определение2: последовательность- чисто периодическая, если =0.

Определение3: вырожденная последовательность- если у неё только конечное число 1-ых знаков отлично от 0.

Утверждение1: любая периодическая последовательность- ЛРП.

Доказательство: по определению1 ,t: U(i++t)-U(i+)=0; (x^t+-x^)U=0; x^(x^t-1)U=0  UpL(x^(x^t-1);

Определение4: наименьшее натуральное t, для которого  : выполняется (1)- период последовательности: Т(U).

Утверждение2: если параметры ,t- удовлетворяют (1), то T(U)t; (U);

Доказательство: 1) l=max((U), ); t=T(U)q+r, 0r<T(U);

 i0 U(i+l+t)=U(i+l); U(i+l+T(U)q+r), a U(i+(U)+T(U))=U(i+(U))  U(i+l+r)=U(i+l)  r=T^/(U)<T(U), но по определению T(U) –наименьший  r=T^/(U)=0 (если r>0 то противоречие с выбором T(U))  t=T(U)q;  T(U)t;

2. пусть (U)>   (U)-1; ((U));

U(i+-1+T(U))=U(i+-1), так как -1+T(U);i:=i+T(U)-1;

U(i+-1+T(U)+(q-1)T(U))=U(i+-1+T(U));

U(i+-1+qT(U))=U(i+-1+t)=U(i+-1), то есть - не наименьший – противоречие с выбором   (U)

Ч.Т.Д.

Утверждение3: если U- периодическая то для любого H(x)P[x]; V=H(x)U- периодический.

Доказательство: H(x)x^(x^t-1)U=0=x^(x^t-1)(H(x)U)=0  V(i++t)= V(i+).

Ч.Т.Д.

Теорема1: пусть U,V- периодические  W=U+V- периодическая и T(W)[T(U),T(V)]; (W)max((U), (V));

Доказательство: пусть max((U), (V))  W(i++)=U(i++)+V(i++)=U(i+(-(U))+(U)+T(U)/T(U))+V(i+(-(V))+(V)+T(V)/T(V))=U(i+)+V(i+)=W(i+);  последовательность периодическая, мы нашли  ,  + утв.2.

Ч.Т.Д.

Следствие1: если (T(U),T(V))=1, то T(W)=T(V)T(U);

Следствие2: если (U)(V), то (W)=max((V), (U));

Доказательство: 1) (T(U),T(V))=1  [T(U),T(V)]=T(V)T(U)  по Т1: T(W)T(V)T(U);

15