Лекции / 2-й семестр / ЛЕКЦИИ~4

Пусть Р- простое и РT(V)T(U)  пусть РT(V) и ;

W(i++)=U(i+)+V(i++)=U(i+)+V(i+);  V(i++)=V(i+)  V(i++)=V(i+)  V(i++)= =V(i++)=V(i+)  по утв.2: противоречие;  T(W)=T(V)T(U).

Ч.Т.Д.

2. пусть (U)<(V)  (U)(V)-1;

(W)<(V)=max((V), (U));

W(i+(V)-1+T(W))=U(i+(V)-1+)+V(i+(V)-1+T(W))=U(i+(V)-1)+V(i+(V)-1+T(W)), a (W)(V)-1  W(i+(V)-1)=U(i+(V)-1)+V(i+(V)-1);

V(i+(V)-1)=V(i+(V)-1+T(W))=V(i+(V)-1+T(V)+T(V))V(i+(V)-1+T(V));  мо определению4: для .

Утверждение4:  U- периодическая однозначно представляется в виде суммы вырожденных и чисто периодических последовательностей.

Доказательство: так как U- периодическая  UpL(x^(x^t-1)), a (x^, x^t-1)=1  L(x^(x^t-1))= =L(x^)+L(x^t-1)  U=U₁+U₂, где U₁- вырожденная, U₂- чисто периодическая.

Ч.Т.Д.

Периодические многочлены.

Определение: многочлен F(x)P[x]- периодический, если  tN, >0: F(x)x^(x^t-1); (1);

Определение: наименьший min{ tN, для которого  : F(x)x^(x^t-1)}=T(F(x));

 если Т- период многочлена, то min{>0: F(x)x^(x^T(F)-1)}=(F(x));

Утверждение: если выполнено (1), то: T(F)t; (F).

Доказательство: так как F(x)x^(F)(x^T(F)-1)  x^(F)(F(x)= x^(F)G(x)), так как в противном случае (F) можно было бы уменьшить, но (F)- min.  G(x)(x^T(F)-1);

Чтобы: x^(F)G(x)x^(x^t-1)  (F) (так как (x^t-1) не делится на x^(F)) 

G(x)(x^T(F)-1)

G(x)x^(F)(x^t-1)  G(x)(x^t-1,x^T(F)-1)=(x^(t,T(F))-1), a (t,T(F))T(F)- если меньше, то это противоречит с выбором T(F).

Определение: многочлен периодический если (F)=0.

Утверждение: F(x)- периодический  e^F- чисто периодическая.

Доказательство: “” F(x)(x^T(F)-1)  F(x)H(x)=x^T(F)-1, a F(x)e^F=0  F(x)H(x)e^F=0

 (x^T(F)-1)e^F=0  e^F- чисто периодическая.

“” если e^F- чисто периодическая, то (x^t-1)e^F=0  e^F(i+t)=e^F(i), a то есть F(x)(x^t-1), F(x)- периодический.

Теорема: пусть F(x)- унитарный многочлен над полем, тоесть Р[х] 

1.  (F), T(F)

2. (F)+T(F)^m-1, где m=degF(x);

3. (F)=0  F(0)0;

Доказательство: 1) 1, x(modF(x)), x²(modF(x)), ……- члены этой последовательности- многочлены вида: с₀+с₁х+…+c_mx^m-1;- остатки от деления на F(x), а таких остатков ^m<, а последовательность – бесконечная  она будет повторяться:

пусть x^j(modF(x))=x^k(modF(x));

F(x)x^j-x^k=x^jk(x^j-k-1);

 (F)jk, T(F)(j-k), то есть  ,F.

2. В нашей последовательности вычетов будут повторы. На куске (F)+T(F)- все вычеты разные, то есть (F)+T(F)^m-1.

3. “” (F)=0  F(x)(x^T(F)-1)  F(x)H(x)= x^T(F)-1; F(0)H(0)=-1  F(0)0;

“” пусть F(0)0  (F(x),x)=1, a F(x)x^(F)(x^T(F)-1)  F(x)(x^T(F)-1)  (F)=0, как наименьшее.

Определение: O(F)=HOK порядков корней многочлена в его поле разложения.

!!! всюду дальше: F(0)0, то есть x неF(x);

O(F)=HOK{ord_j, F(_j)=0}.

Теорема: пусть F(x) – неприводимый многочлен над полем P=GF(q); degF(x)=m;  T(F)=O(F); T(F)q^m-1;

Доказательство: a) пусть корни F(x): ₁…_m в GF(q^m);

F(x)(x^T(F)-1)  F(x)H(x)= x^T(F)-1  F(_j)H(_j)=ord_jT(F), то есть m- чисел, каждое делит T(F)  O(F)T(F).

b) любой корень многочлена F(x) удовлетворяет уравнению:

x^O(F)-1=0  (x-_j)(x^O(F)-1)  , a все _j попарно различные  (x-_j) (x^O(F)-1)  F(x)(x^O(F)-1)  T(F)O(F).

a)+b)  T(F)=O(F);

Корни F(x): ₁…_m – образуют мультипликативную группу поля, а порядок каждого делит порядок группы: O(F)q^m-1.

Определение: если O(F)q^m-1; degF(x)=m; F(x)- над P=GF(q), то F(x)- многочлен максимального периода.

Теорема: GF(q), q=pⁿ- характеристика поля;

Пусть где G₁(x), …, G_t(x)- попарно различные неприводимые многочлены.

DegG(x)=m_j  T(F(x))=O(F)p^c, где

Доказательство: F(x)(x^T(F)-1)  G_j(x)(x^T(F)-1)  O(G_j)T(F),  j= 

HOK{ O(G_j), j=}T(F); так как все различны и неприводимый x^T(F)-1  G_j(x) (x^О(F)-1);

G₁(x)…G_t(x) (x^О(F)-1)  (G₁…G_t)H(x)= (x^О(F)-1); (G₁…G_t)H (x)=(x^О(F)-1) = x^О(F)-1;

, a F(x)(G₁…G_t), так как , a (G₁…G_t) x^О(F)-1  T(F)O(F)p^c;

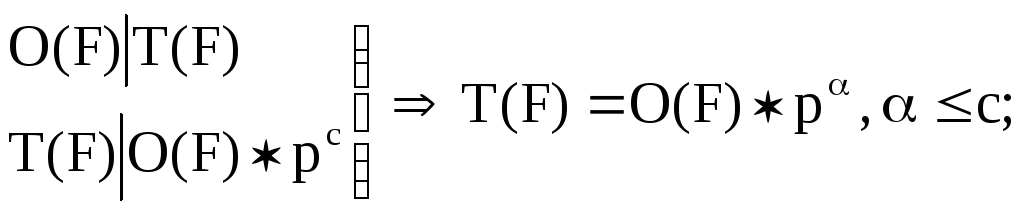
пусть <c  c-1  T(F) )O(F)p^c-1, но этого не может быть: пусть

a (x^O(F)-1)^/=O(F)x^O(F)-1 пусть в роле -F(x)- раскладывается на линейные множители и корни F(x) в этом поле образуют мультипликативную группу этого поля и ord  максимальная кратность корня = p^c-1, а по условию - противоречие  T(F)= O(F)p^c-1.

Пример: (x+1)⁵(x²+x+1)³(x³+x+1)(x³+x²+1)²; GF(2)

все многочлены неприводимые:

1. корни

1. (x+1)  1, ord1=1

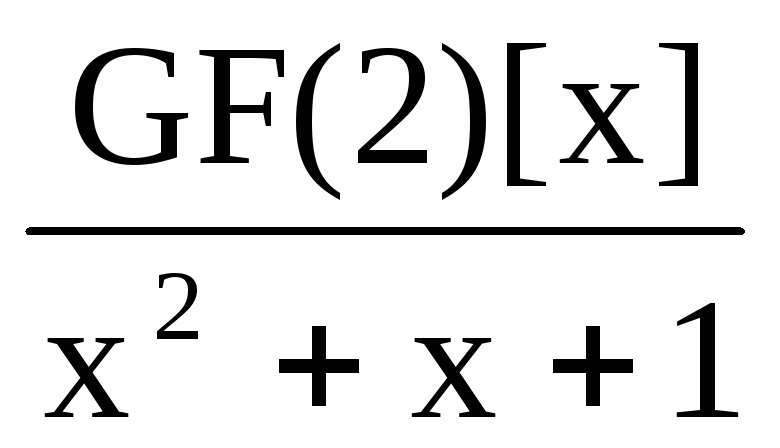2. пусть - корень  ²++1=0; ord=3;

3. x³+x+1-пусть корень , GF(2³) ³++1=0; 1, ord=7

4. x³+x²+1  ord=7 (аналогично).

Для degF(x)=m  T(F)=q^m-1;

Теорема: T(F)=q^m-1  F(x)- неприводимый; ord= q^m-1 ;

Доказательство: “” F(x)=

T(F)=O(F)p^c=q^m-1; так как (p, q^m-1)=1  c=0  F(x)=то есть r_j=1;

O(G_j)

q^m-1=O(F)=HOK;

- противоречие,  F(x)=G(x)  неприводимый; T(F)=ord=q^m-1;

“” просто проверка, что такие многочлены имеют такой Т.

Выборки из линейных рекуррент.

Определение: пусть U^- последовательность V- (l, d)- выборка, если V(i)=U(l+d_i).

Утверждение:

Доказательство: V(i) =U(l+d(i+))=U(l+d_i+T(U) )=U(l+ d_i)=V(i);

Теорема: пусть F(x)- неприводимый над Р: degF(x)=m; UpL(F); V-(l-d)-выборка из U;

 VpL(F(x)), degG(x)m;

Доказательство: пусть - корень F(x) вGF(q^m)  U(i)=

V(i)=U(l+d_i)=

Вообще:

17