Лекции / 2-й семестр / ЛЕКЦИИ~1

Лекция.

1. Z_p – поле.

2. Если f(x) – непрерывен над Р, то 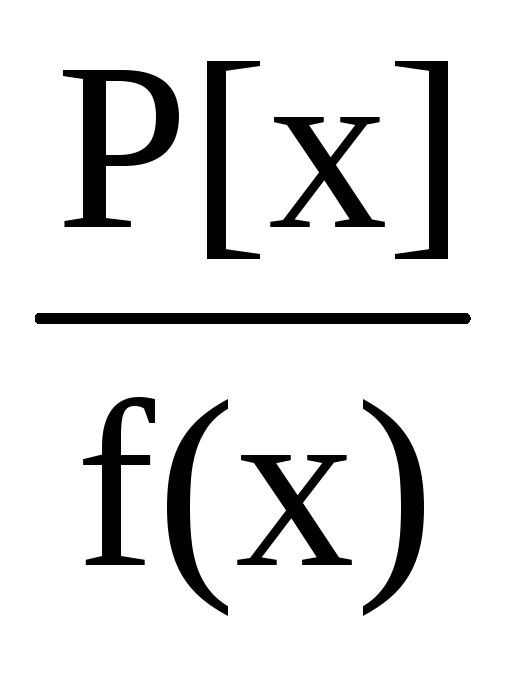- поле и

Покажем:

Утверждение: пусть Р – конечное поле, тогда ;

Доказательство: 1. РР₀ = {0, e, 2e, …, (p-1)e}, где р – характеристика поля Р: р=char P;

2. ₁P\{0};

₂P\I₁; I₁={₁C₁\C₁P₀};

₃P\I₂; I₂={₁C₁ + ₂C₂\C₁C₂P₀};

…………………………………….….

_k+1P\I_k;

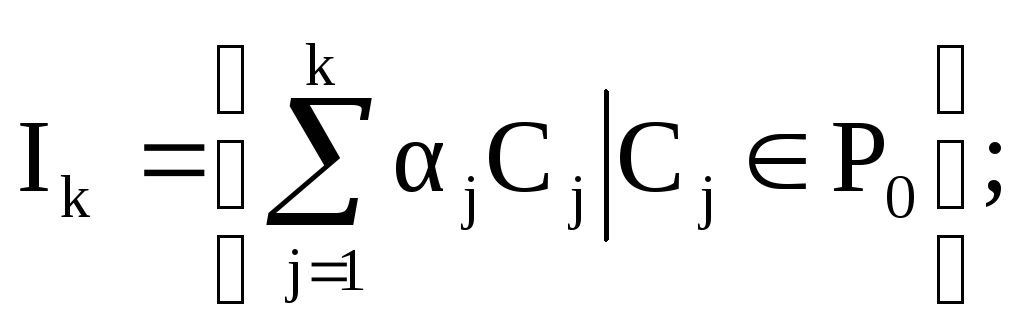
Пусть _t – последний, который удалось выбрать, то есть Р\I_t=   xP,

Для того, чтобы доказать: осталось доказать, что все такие суммы попарно различны.

От противного: пусть (С_1, …, С_t)(С_1, …, то есть отличаются хотя бы в одной координате.

Пусть С_t, С_t-1 - первое несовпадение.

 - это противоречит выбору _s  не существует две равные суммы  все такие суммы попарно различны и задают различные элементы поля. Число таких сумм равно числу элементов поля и равно р^t;

Теорема: пусть Р – конечное поле, над которым раскладывается на линейные множители, тогда - поле из р^t элементов.

Доказательство: f(x)=; f^/(x)=-e;  (f(x), f^/(x))=1  f(x) – не имеет кратных корней, то есть они все различны  корней f(x)=р^t.

Пусть ,  - корни f(x)  - корень f(x).

+ - ? (+)^р = ^р + 

Ч.Т.Д.

 Вывод: корни многочлена f(x) – образуют поле (ассоциативность, дистрибутивность выполняются).

Следствие: Q<P, где Q – подполе Р;

Доказательство: все элементы Р – корни многочлена , так как Q – подполе  характеристика та же  все элементы Q корни многочлена , а

d=(t, d)  d/t; так как корни НОДа совпадают с корнями , так как:

{Лемма: (а_х, b_x) = (a_xc_xb_x, b_x);}

; то есть алгоритм Евклида для показателей.

Теорема “О примитивном элементе”: пусть   Р: ord=p^t–1;

Доказательство: Р^=Р\{O}; P^ - комм. группа 

1. expP^=NOK{ord, P^};

2.  : ord=expP^;

Пусть P^  все элементы Р^ - корни многочлена ;

Число элементов:

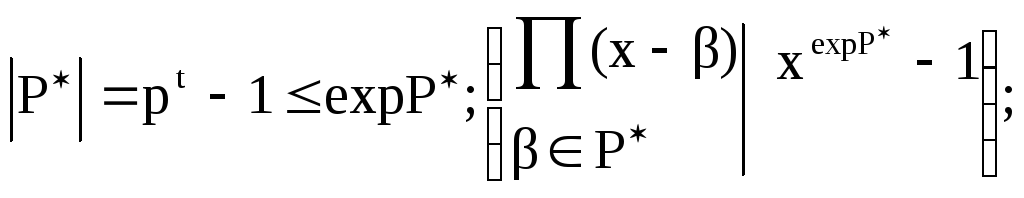
Определение: элемент порядок которого равен мощности поля без единицы называется примитивным элементом поля:

Следствие: пусть  - примитивный элемент поля   Р\О,  = ^k;

Доказательство: , ², …, все элементы различны.

Теорема: пусть (q – простое число или его степень), f(x) – неприводимый над Р, degf(x)=n   Q>P:  Q: f()=0. При этом все различные корни f(x) в Q имеют вид:

Доказательство:

1. Покажем, что такое поле Q существует:

пусть ;

пусть с₁=…=с_n-1  {с₀с₀Р}=Р  Р Q;

пусть хQ; f(x)0(modf(x)) – по определению  х – f(x);

2. Q>P, Q, f()=0, пусть

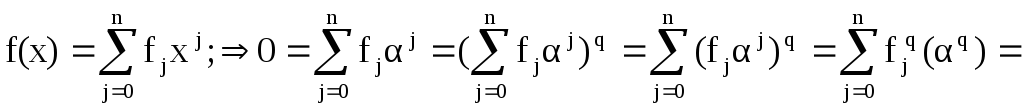
корень корни.

Осталось доказать, что все они различны:

корни f(x);

пусть среди корней есть совпадения: 

(- то есть минимальное k с таким свойством)

, а

kn; ;

Берём коэффициент (один). Надо доказать, что он из поля Р:

{(-1)^k-s=-1, так как q – нечётное число};

если i_k-s<k-1 то показатель увеличивается на 1

если i_k-s=k-1 то , то есть слагаемые

,

а слагаемые то есть возведение в степень q приводит просто к перестановке слагаемых в сумме, то есть  коофициент многочлена остаётся на месте  g(x)P[x], а g(x)f(x), 0<degg(x)<n – противоречие с неприводимостью f(x)  k=n  . Ч.Т.Д.

Примечание:

пусть Р₀=Z_р; Р₀<Р₁; f₁(x) – имеет корень в Р₁  Р₁<Р₂; аналогично f₂(x) – имеет корень и т.д.  за конечное число шагов мы разложим в произведении над каким-нибудь полем.

1. Берём поле Р₀<Р₁ и многочлен f₁(x) раскладываем на линейные множители в Р_1.

2. Берём Р₁<Р₂ и f₂(x) ……………………

………………………………………………

11. Р_k<Р_k+1 и f_k+1(x) ………………………...

На S-ом шаге получим поле, над которым многочлен раскладывается на линейные множители.

Определение: пусть Q>P; унитарный многочлен f(x) наименьшей степени с коэффициентами из Р , такой что для  Q, f()=0 – минимальный многочлен элемента  над полем Р: m_,P(x);

Утверждение: пусть Q>P, Q,  m_,P(x) – неприводимый.

Доказательство: пусть m_,P(x)=f(x)g(x); 0<degf(x)<degm_,P(x); m_,P()=f()g()=0; либо f() либо g() равны 0, но degf и degg < m_,P – противоречие с определением линейного многочлена  предположение о разложении неверно.

Ч.Т.Д.

Теорема: пусть Р – конечное поле Р=q=p^t   n  f(x)P[x]:

11. Degf(x)=n;

2. f(x) – неприводим.

Доказательство: qⁿ=p^tn; Q – поле из такого количества элементов, что  это поле из корней многочлена: , где Q>P;

Рассмотрим все поля G_k вида: Q> G_k, k – простое и kn  G_k - поле из элементов.

.{2p₁p₂…..p_t>2^t+1  число простых делителей натурального числа строго меньше чемlog₂n}

 Q\ m_,P(x) – неприводим. Все его корни имеют вид: , ^q, …,  если k<n то m_,P(x) – имеет корень в поле из q^k элементов, то есть этот корень лежит в каком-то собственном подполе Q, то есть в одном из G_k – противоречие  k=n, то есть получили неприводимый многочлен deg=n  m_,P(x).

Отображение “след”.

Определение: пусть есть поле Р из q элементов и поле Р^/ из q^m элементов. Отображение называется “следом” если:

Теорема: 1.

2. - минимальное отображение над GF(q); пусть a,b  GF(q);

3. km

Доказательство: чтобы доказать, что надо доказать, что

Проверим свойство линейности:

Докажем последний пункт теоремы:

[обозначим через q₁=q^k; ] =

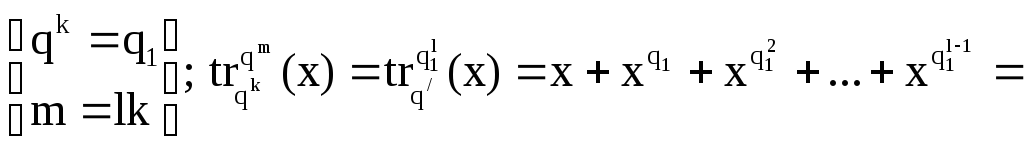
1. j₂j₁  j₂-j₁0; j₂-j₁>0; k-1 j₂-j₁k – противоречие 1.

2. j₂=j₁;  s₁=s₂; мы доказали, что в множестве нет одинаковых элементов.

k-1+k(m/k –1)=m-1; 0, 1, 2, 3, ….., m-1

Теорема:  отображение конечного поля в себя может быть задано многочленом.

Доказательство: GF(q)={0, ₁, …, _q-1}

f: GF(q)  GF(q); f(_i)=_i;

Свойство: (x-)^q-1; y^q=y; y(y^q-1-1)=0; y^q-1=1,; yGF(q)0; 1-(x-)^q-1=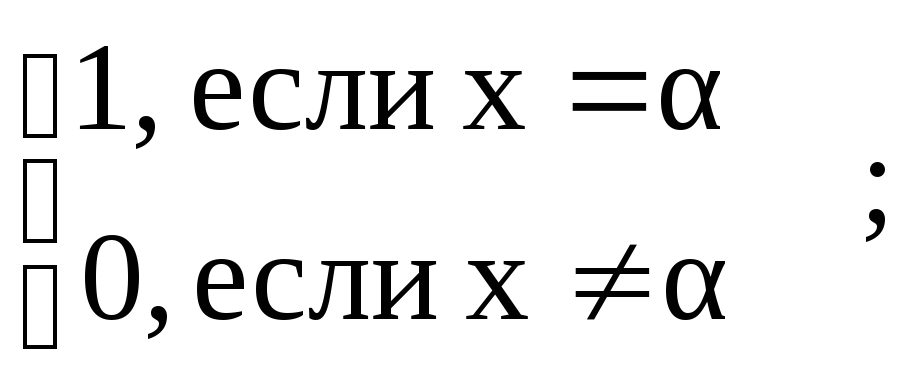

Семинар.

1. GF(2). Доказать, что неприводим: х⁵+х+1.

Корней нет в GF(2), то есть “0” или “1”  неприводим, так как deg(х) 3.

2. 

с₀+с₁x+c₂x²+c₃x³+c₄x⁴  с₀+с₁+c₂²+c₃³+c₄⁴; [x]=; c_i{0,1};  - класс элемента х;

0=⁵+²+1=[х]⁵+[х]²+1=[х⁵+х²+1] класс многочлена х⁵+х²+1 – это класс 0.

Пример: [х⁵+х²+1]=[0]

х⁴+х+1; GF(2); ⁴=+1; (1++²)+(+³)=?; (1++²)(+³)=?;

(1+Q+Q²)+(Q+Q³)=Q³+Q²+1 (в GF(2)); (1+Q+Q²)(Q+Q³)=Q+1;

Q⁵=QQ⁴=Q(Q+1);

3. Подсчитаем “след” от элемента: +1;

4. Берём любой элемент, возводим в степень 15. Ответ должен равняться 1, проверим это:

I: (Q²+Q³)¹⁵=Q³⁰(Q+1)¹⁵; Q³⁰=Q²Q^47=Q²(Q+1)⁷;

II: (Q+1)^q=(Q+1)⁸⁺¹=(Q+1)(Q+1)⁸=(Q+1)(Q⁸+1)=(Q+1)((Q+1)²+1)=Q²(Q+1);

(Q+1)¹⁵=(Q+1)(Q+1)²(Q+1)⁴(Q+1)⁸=(Q+1)(Q²+1)(Q⁴+1)(Q⁸+1)=(Q+1)(Q²+1)(Q+1+1)((Q+1)²+1)= =(Q+1)(Q²+1)(Q)(Q²)=(Q³+Q+Q²+1)Q³=Q⁶+Q⁵+Q⁴+Q³=Q²(Q+1)+(Q+1)+Q(Q+1)+Q³=Q³+Q²+Q+ +1+Q²+Q+Q³=1.

5. GF(s); -; 1-(x-)⁴ – выпишем многочлен:

 3(1-(х⁴))+4(1-(х-1)⁴)+2(1-(х-3)⁴)+2(1-(х-4)⁴);

6. GF(s); 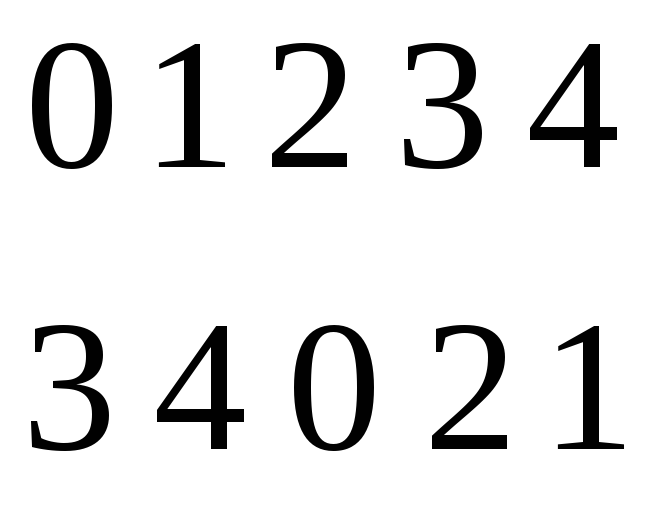; докажем что х⁴ существует:

1-(х-)⁴  3(1-(х⁴))+4(1-(х-1)⁴)+2(1-(х-3)⁴)+1(1-(х-4)⁴);

В общем случае:

7. Построить поле из q элементов:

GF(3), x²+ax+b; x²+x+2;

[x]=; ²=--2; ²++2=0;

перемножим элементы: =²=--2;

c₀+c₁+c₂²+c₃³(c₀ c₁ c₂ c₃);

b₀+b₁+b₂²+b₃³, раскрываем скобки: c_jb_j^i+j; ^i+j=^k=

(b₀ b₁ b₂ b₃): b_jc_j_i+j; если две 1, то прибавляем к результату;

если одна 1, то никуда не идёт.

Умножаем на  и всё сдвигаем:

(с₀+с₁+с₂²+с₃³)(с₀ с₁ с₂ с₃)+ (с₀…с₃)=(0, с₀, с₁, с₂)+с₃(1, 1, 0, 0);

Как строим вектора:

⁰=1;

;^m=(0, _m-1);

^m=c_m-1^m-1+….+c₀;

8. Построим векторы для поля:

GF(2): x⁴+x+1; ⁴=+1; 1=c₀+c₁+c₂²+c₃³;

5