Координатные плоскости, рекуррент над полем.

GF(q); q=p²; deg f(x)=r;

элементы поля ;

Элементы : 1,, ^r, …, ^r-1 – базис

Пусть ₀ ₁ …_r-1 – некоторый базис поля

U – ЛПР;

Определение: последовательность значений (U_j(0), U_j(1), …) – j-ая координатная последовательность ЛРП U в базисе  :

Теорема: пусть U-ЛРП максимального периода порядка m ( то есть deg F(x)=m ) над полем GF(q)   базиса = (₀…_r-1) – базис поля

1. U_j – ЛРП – максимального периода над полем GF(p) степени r^m;

2. U₀, …, U_r-1 – ЛНз над GF(p);

3.  j,k U_j – сдвиг U_k на число шагов кратное :

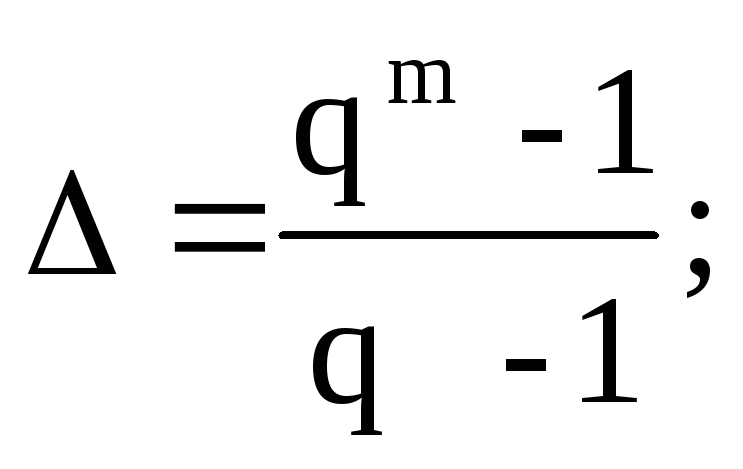
Доказательство:

Определение: базис = (X₀…X_r-1) – двойственный к базису , если : ;

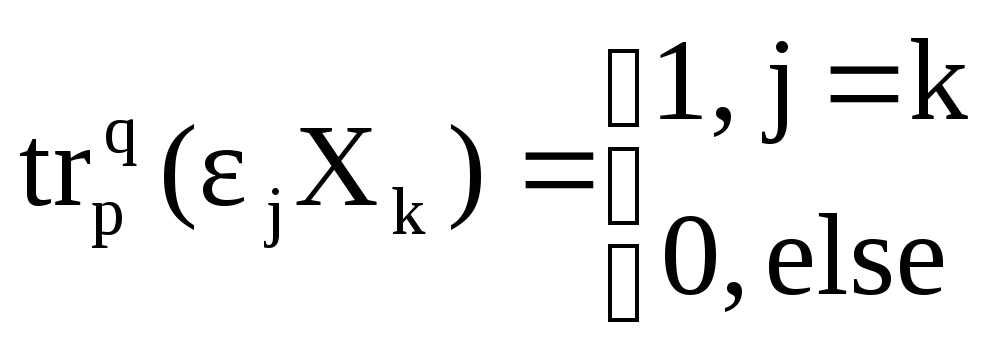( Для каждого базиса существует к нему двойственный ).

1. Пусть - корень в GF(q^m) 

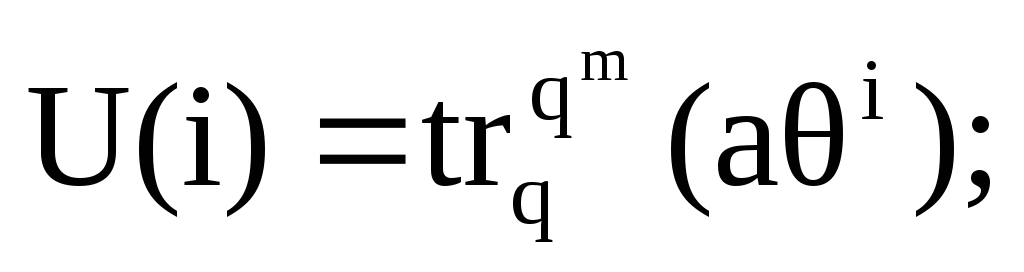
С другой стороны:

ord= q^m-1 = p^2m-1; корень некоторого многочлена GF(p)(x)  G(x) степени rm (то есть примитивный элемент мультипликативной группы поля GF(q^m)) 

T(G) = ord p^2m –1; G(x) = m_GF(p)(x);

2. Пусть все координатные плоскости ЛЗ   С₀,…С_r-1 : не все равные0.

- возможно в том и только в том случае, когда a=0, a0  - последнее  С_j=0, j , но мы предположили, что не все С=0  противоречие.

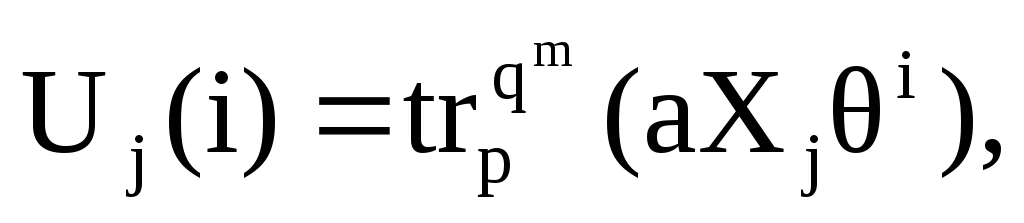3. так как  - примитивный элемент поля   l : X_j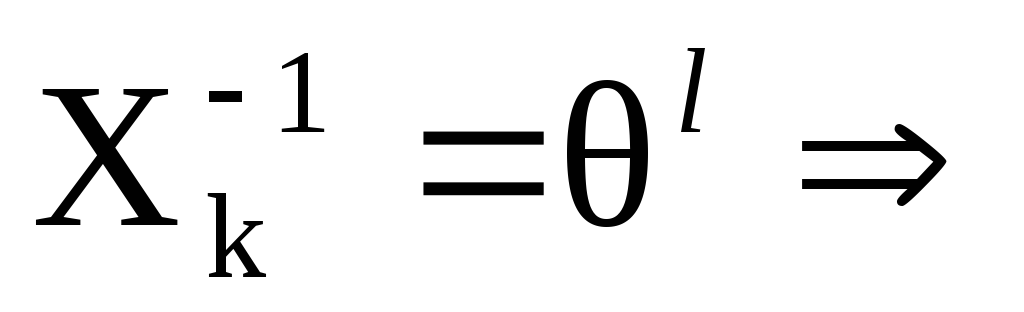 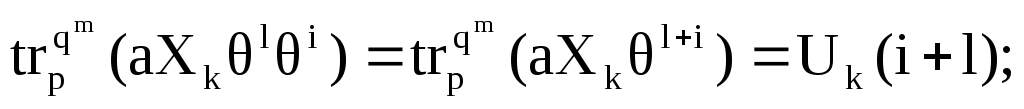то есть сдвиг на l шагов.

, а 

. Ч.Т.Д.

Пусть  - корень f(x), degf(x)=r над GF(p)[x]  {1, , ², …, ^r+1} – базис  H(i)=H_j(i)^j;

Произведение ЛРП на её сдвиг.

Пусть U-ЛРП;

V(i) = f(H(i) … U(i+m+1));

Пусть V(i) = U(i)U(i+k);

Опишем вид минимального многочлена произведения ЛРП максимального периода на её сдвиг, то есть U-ЛРП максимального периода над GF(q), f(x), degf(x) = m;

Пусть  - корень f(x) вGF(q)

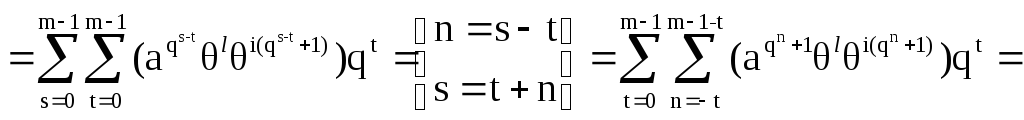{так как

Так как предел суммирования от (-t) до (m-1-t), то можно его заменить на от (0) до (m-1) }=

= возьмём элемент:  элементы: корни неприводимого многочлена.

0 1 2 m-2 m-1 , то есть все слагаемые разбиваются на пары ( или почти все).

Пусть m = 2+1;

;

Пусть m = 2 

0 1 2 -1  +1 m-1 остаётся  без пары  V(i)= ------ +

последний след можно переписать;

Теорема: пусть U-ЛРП над GF(q), c f(x), degf(x) = m,  - корень многочлена f(x) в его поле разложения GF(q^m), a – параметр, задаваемый начальным вектором U;

 последовательность V определяется равенством:

V(i) = U(i)U(i+l) – имеет f-ное представление вида: m = 2;

Следствие: пусть в условиях теоремы

Доказательство: в теореме получено f-ное представление V в виде суммы ЛРП-ей с попарно- различными неприводимыми множествами  m_V(x) = произведению тех неприводимых множеств, у которых соответствующие коофициенты не равны нулю. (^l + ^lqⁿ)0

20