Лекции / Лекции Кузьмина / WORD6~1 / ЛЕКЦИИ~1

Лекция.

1. Z_p – поле.

2. Если f(x) – непрерывен над Р, то - поле и

Покажем:

Утверждение: пусть Р – конечное поле, тогда ;

Доказательство: 1. РÉР₀ = {0, e, 2e, …, (p-1)e}, где р – характеристика поля Р: р=char P;

2. a₁ÎP\{0};

a₂ÎP\I₁; I₁={a₁C₁\C₁ÎP₀};

a₃ÎP\I₂; I₂={a₁C₁ + a₂C₂\C₁C₂ÎP₀};

…………………………………….….

a_k+1ÎP\I_k;

Пусть a_t – последний, который удалось выбрать, то есть Р\I_t=Æ ~ " xÎP,

Для того, чтобы доказать: осталось доказать, что все такие суммы попарно различны.

От противного: пусть (С_1, …, С_t)¹(С_1, …, то есть отличаются хотя бы в одной координате.

Пусть С_t¹, С_t-1¹ - первое несовпадение.

Þ - это противоречит выбору a_s Þ не существует две равные суммы Þ все такие суммы попарно различны и задают различные элементы поля. Число таких сумм равно числу элементов поля и равно р^t;

Теорема: пусть Р – конечное поле, над которым раскладывается на линейные множители, тогда - поле из р^t элементов.

Доказательство: f(x)=; f^/(x)=-e; Þ (f(x), f^/(x))=1 Þ f(x) – не имеет кратных корней, то есть они все различны Þ корней f(x)=р^t.

Пусть a, b - корни f(x) Þ - корень f(x).

a+b - ? (a+b)^р = a^р + Þ

Ч.Т.Д.

Þ Вывод: корни многочлена f(x) – образуют поле (ассоциативность, дистрибутивность выполняются).

Следствие: Q<P, где Q – подполе Р;

Доказательство: все элементы Р – корни многочлена , так как Q – подполе Þ характеристика та же Þ все элементы Q корни многочлена , а

d=(t, d) Þ d/t; так как корни НОДа совпадают с корнями , так как:

{Лемма: (а_х, b_x) = (a_x*c_x*b_x, b_x);}

; то есть алгоритм Евклида для показателей.

Теорема “О примитивном элементе”: пусть Þ $ aÎР: orda=p^t–1;

Доказательство: Р^*=Р\{O}; P^* - комм. группа Þ

1. expP^*=NOK{ordb, bÎP^*};

2. $ a: ord=expP^*;

Пусть bÎP^* Þ все элементы Р^* - корни многочлена ;

Число элементов:

Определение: элемент порядок которого равен мощности поля без единицы называется примитивным элементом поля:

Следствие: пусть a - примитивный элемент поля Þ " bÎР\О, b = a^k;

Доказательство: a, a², …, все элементы различны.

Теорема: пусть (q – простое число или его степень), f(x) – неприводимый над Р, degf(x)=n Þ $ Q>P: $ aÎQ: f(a)=0. При этом все различные корни f(x) в Q имеют вид:

Доказательство:

1. Покажем, что такое поле Q существует:

   пусть ;

   пусть с₁=…=с_n-1º0 Þ {с₀½с₀ÎР}=Р Þ РÌ Q;

   пусть хÎQ; f(x)º0(modf(x)) – по определению Þ х – f(x);

2. Q>P, aÎQ, f(a)=0, пусть

корень корни.

Осталось доказать, что все они различны:

корни f(x);

пусть среди корней есть совпадения: Þ

(- то есть минимальное k с таким свойством)

, а

k½n; ;

Берём коэффициент (один). Надо доказать, что он из поля Р:

{(-1)^k-s=-1, так как q – нечётное число};

если i_k-s<k-1 то показатель увеличивается на 1

если i_k-s=k-1 то , то есть слагаемые

,

а слагаемые то есть возведение в степень q приводит просто к перестановке слагаемых в сумме, то есть " коофициент многочлена остаётся на месте Þ g(x)ÎP[x], а g(x)½f(x), 0<degg(x)<n – противоречие с неприводимостью f(x) Þ k=n Þ . Ч.Т.Д.

Примечание:

пусть Р₀=Z_р; Р₀<Р₁; f₁(x) – имеет корень в Р₁ Þ Р₁<Р₂; аналогично f₂(x) – имеет корень и т.д. Þ за конечное число шагов мы разложим в произведении над каким-нибудь полем.

1. Берём поле Р₀<Р₁ и многочлен f₁(x) раскладываем на линейные множители в Р_1.

2. Берём Р₁<Р₂ и f₂(x) ……………………

………………………………………………

11. Р_k<Р_k+1 и f_k+1(x) ………………………...

    На S-ом шаге получим поле, над которым многочлен раскладывается на линейные множители.

    Определение: пусть Q>P; унитарный многочлен f(x) наименьшей степени с коэффициентами из Р , такой что для " aÎQ, f(a)=0 – минимальный многочлен элемента a над полем Р: m_a,P(x);

    Утверждение: пусть Q>P, aÎQ, Þ m_a,P(x) – неприводимый.

    Доказательство: пусть m_a,P(x)=f(x)g(x); 0<degf(x)<degm_a,P(x); m_a,P(a)=f(a)g(a)=0; либо f(a) либо g(a) равны 0, но degf и degg < m_a,P – противоречие с определением линейного многочлена Þ предположение о разложении неверно.

    Ч.Т.Д.

    Теорема: пусть Р – конечное поле ½Р½=q=p^t Þ " n $ f(x)ÎP[x]:

12. Degf(x)=n;

2. f(x) – неприводим.

Доказательство: qⁿ=p^tn; Q – поле из такого количества элементов, что $ это поле из корней многочлена: , где Q>P;

Рассмотрим все поля G_k вида: Q> G_k, k – простое и k½n Þ G_k - поле из элементов.

.{2*p₁*p₂…..p_t>2^t+1 Þ число простых делителей натурального числа строго меньше чемlog₂n}

$ aÎQ\ m_a,P(x) – неприводим. Все его корни имеют вид: a, a^q, …, Þ если k<n то m_a,P(x) – имеет корень в поле из q^k элементов, то есть этот корень лежит в каком-то собственном подполе Q, то есть в одном из G_k – противоречие Þ k=n, то есть получили неприводимый многочлен deg=n Þ m_a,P(x).

Отображение “след”.

Определение: пусть есть поле Р из q элементов и поле Р^/ из q^m элементов. Отображение называется “следом” если:

Теорема: 1.

2. - минимальное отображение над GF(q); пусть a,b Î GF(q);

3. k½m

Доказательство: чтобы доказать, что надо доказать, что

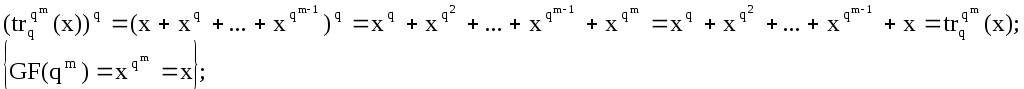
Проверим свойство линейности:

Докажем последний пункт теоремы:

[обозначим через q₁=q^k; ] =

1. j₂¹j₁ Þ j₂-j₁¹0; j₂-j₁>0; k-1³ j₂-j₁³k – противоречие 1.

2. j₂=j₁; Þ s₁=s₂; мы доказали, что в множестве нет одинаковых элементов.

k-1+k(m/k –1)=m-1; 0, 1, 2, 3, ….., m-1

Теорема: " отображение конечного поля в себя может быть задано многочленом.

Доказательство: GF(q)={0, a₁, …, a_q-1}

f: GF(q) Þ GF(q); f(a_i)=b_i;

Свойство: (x-a)^q-1; y^q=y; y(y^q-1-1)=0; y^q-1=1,; yÎGF(q)½0; 1-(x-a)^q-1=

Семинар.

1. GF(2). Доказать, что неприводим: х⁵+х+1.

   Корней нет в GF(2), то есть “0” или “1” Þ неприводим, так как dega(х)£ 3.

2. 

   с₀+с₁x+c₂x²+c₃x³+c₄x⁴ ~ с₀+с₁q+c₂q²+c₃q³+c₄q⁴; [x]=q; c_iÎ{0,1}; q - класс элемента х;

   0=q⁵+q²+1=[х]⁵+[х]²+1=[х⁵+х²+1] класс многочлена х⁵+х²+1 – это класс 0.Þ

   Пример: [х⁵+х²+1]=[0]

   х⁴+х+1; GF(2); q⁴=q+1; (1+q+q²)+(q+q³)=?; (1+q+q²)(q+q³)=?;

   (1+Q+Q²)+(Q+Q³)=Q³+Q²+1 (в GF(2)); (1+Q+Q²)(Q+Q³)=Q+1;

   Q⁵=QQ⁴=Q(Q+1);

3. Подсчитаем “след” от элемента: q+1;

   

   

4. Берём любой элемент, возводим в степень 15. Ответ должен равняться 1, проверим это:

   I: (Q²+Q³)¹⁵=Q³⁰(Q+1)¹⁵; Q³⁰=Q²Q^4*7=Q²(Q+1)⁷;

   II: (Q+1)^q=(Q+1)⁸⁺¹=(Q+1)(Q+1)⁸=(Q+1)(Q⁸+1)=(Q+1)((Q+1)²+1)=Q²(Q+1);

   (Q+1)¹⁵=(Q+1)(Q+1)²(Q+1)⁴(Q+1)⁸=(Q+1)(Q²+1)(Q⁴+1)(Q⁸+1)=(Q+1)(Q²+1)(Q+1+1)((Q+1)²+1)= =(Q+1)(Q²+1)(Q)(Q²)=(Q³+Q+Q²+1)Q³=Q⁶+Q⁵+Q⁴+Q³=Q²(Q+1)+(Q+1)+Q(Q+1)+Q³=Q³+Q²+Q+ +1+Q²+Q+Q³=1.

5. GF(s); -a; 1-(x-a)⁴ – выпишем многочлен:

   å 3(1-(х⁴))+4(1-(х-1)⁴)+2(1-(х-3)⁴)+2(1-(х-4)⁴);

6. GF(s); ; докажем что х⁴ существует:

   1-(х-a)⁴ Þ 3(1-(х⁴))+4(1-(х-1)⁴)+2(1-(х-3)⁴)+1(1-(х-4)⁴);

   В общем случае:

7. Построить поле из q элементов:

   GF(3), x²+ax+b; x²+x+2;

   [x]=q; q²=-q-2; q²+q+2=0;

   перемножим элементы: q*q=q²=-q-2;

   c₀+c₁q+c₂q²+c₃q³~(c₀ c₁ c₂ c₃);

   b₀+b₁q+b₂q²+b₃q³, раскрываем скобки: c_jb_jq^i+j; q^i+j=q^k=

   

   (b₀ b₁ b₂ b₃): åb_jc_ja_i+j; если две 1, то прибавляем к результату;

   если одна 1, то никуда не идёт.

   Умножаем на q и всё сдвигаем:

   q(с₀+с₁q+с₂q²+с₃q³)~(с₀ с₁ с₂ с₃)+ q(с₀…с₃)=(0, с₀, с₁, с₂)+с₃(1, 1, 0, 0);

   Как строим вектора:

   q⁰=1;

   ;a^m=(0, a_m-1);

   q^m=c_m-1q^m-1+….+c₀;

8. Построим векторы для поля:

GF(2): x⁴+x+1; q⁴=q+1; 1=c₀+c₁q+c₂q²+c₃q³;

; ;
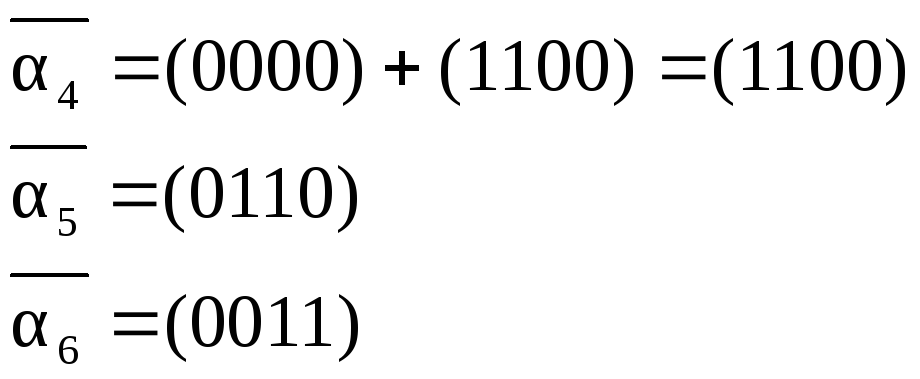