Лекции / Лекции Кузьмина / WORD6~1 / ЛЕКЦИИ~2

Перемножим:

b₀c₀+b₀c₁+b₀c₂+b₀c₃+b₁c₀+…++++++=(0100)+(0010)+ +(1100)+(0110)=(1100) по (mod2).

Линейные рекуррентные последовательности.

Последовательность над полем Р – произвольное отображение множества N₀ в поле Р:

U: N₀®P; U=(H(0), U(1), U(2), …);

P^¥ - всё множество последовательностей над Р.

Линейная рекуррентная последовательность (ЛРП) над Р – последовательность U для которой $ mÎN, c₀, c₁, …, c_m-1ÎP: " i ³0 :

Отрезок последовательности: (U(c), …, U(m-1)) – начальный вектор рекуррентна.

Определение: - характеристический многочлен последовательности.

Порядок рекуррентны = deg(F(x));

Пример1: ГПр – ЛРП: b_n+1=qb_n; F(x)=x-q;

Пример2: АПр Þ а_n+1=a_n+d=a_n+(a_n-a_n-1); Þ a_n+2=2a_n+1-a_n; F(x)=x²-2x+1=(x-1)²;

Пример3: Фибоначчи: U_n+2=U_n+1+U_n; 1,1,2,3,5,8,11,…; F(x)=x²-x-1;

Утверждение: ЛРП U с характеристическим многочленом F(x), degF(x)=m – однозначно определяется своим начальным вектором длины m.

Следствие: число рекуррент (с F(x): degF(x)=m) =½P½^m;

Обозначение: множество всех ЛРП над Р с характеристическим многочленом F(x): pL(F).

Операции над последовательностями.

1. W=U+V; то есть: W(i)=U(i)+V(i);

2. CÎP, W=CU; W(i)=CU(i);

Утверждение: pL(F) – абелева группа, замкнутая относительно операции умножения на элементы Р (то есть ВПр-во).

Доказательство: 1. Замкнутость относительно ±, то есть W=(U-V)Î pL(F);

то есть WÎ pL(F);

2. Замкнутость относительно * на СÎР:

h(i+m)=CU(i+m)=åc_j(CU(i+j))=åc_jW(i+j);

Ч.Т.Д.

Определение: последовательности U₁, …, U_m Î pL(F) – базис семейства ЛРП с характеристическим многочленом F(х), если:

1. VÎpL(F) $ c₁, …, c_m: V=c₁U₁+…+c_mU_m;

2. Константы c₁, …, c_m – определены однозначно, то есть представление 1. – однозначно.

Утверждение: U₁, …,U_m – базис Û

1. " VÎpL(F) $ c₁, …, c_m : V=c₁U₁+…+c_mU_m;

2. c₁U₁+…+c_mU_m=0 Þ c₁=c₂=…=c_m=0.

Доказательство: “Þ”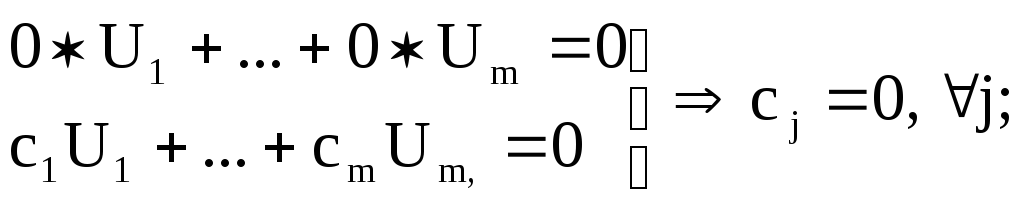

“Ü” пусть

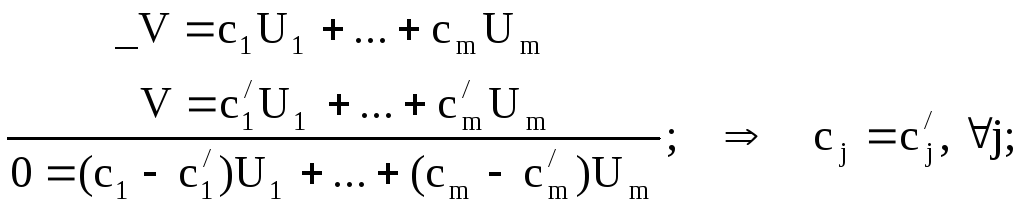
Ч.Т.Д.

Пусть е_k – последовательность ÎpL(F): её начальный вектор длины m: , то есть (е(₀), е(₁), …, 0, …, е(_m-1)) – начальный вектор последовательности е_k.Þ

(U(0), …, U(m-1)) Þ

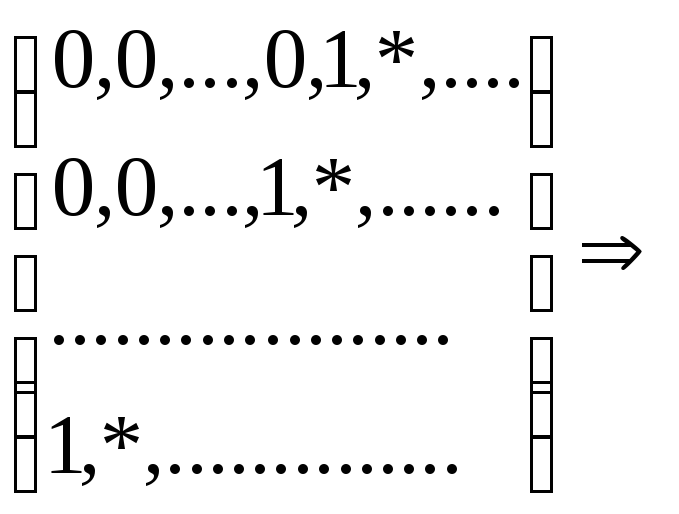
Теорема: последовательности U₁, …, U_m - -базис Û, то есть определитель из начальных векторов не равен 0.

Доказательство: от противного: пусть ½А½=0, тогда :

“Þ” - это уравнение имеет ненулевое решение: (c₁, …,.c_m)= Þ

то есть пусть V=åc_jU_jÎ pL(F), где V¹0 – начальный вектор.

Þ V=0 – нулевая последовательность Þ по утверждению о базисе: U₁, …,U_m – не базис.

“Ü”½А½¹0 Þ - такая система линейных уравнений однозначно разрешима для любого вектора V. Пусть (c₁, …, c_m)- решение Þ ЛРП VÎpL(F), V=åc_jU_j;

Ч.Т.Д.

Определение: пусть UÎР^¥, h(x)=;

Þ произведение последовательности U на многочлен h(x) – последовательность W=h(x)*U;

Пример: x*(U(0), U(1), U(2), …)=(U(1), U(2), …)

Свойства умножения последовательности на многочлен.

1. (A(x)+B(x))U=A(x)U+B(x)U;

2. (A(x)B(x))U=A(x)*(B(x)U);

3. A(x)(U+V)=A(x)U+A(x)V;

Теорема: pL(F)={UÎP^¥: F(x)U=0};

Доказательство: UÎ pL(F) Û U(i+m)=åc_jU(i+j) Û U(i+m)-åc_jU(i+j)=0 Û F(x)U=0;

Утверждение: UÎ pL(F) Þ " A(x), A(x)UÎ pL(F);

Доказательство: F(x)*(A(x)U)=(F(x)A(x))*U=(A(x)F(x))*U=A(x)*(F(x)U)=A(x)*0=0.

Следствие: " ЛРП имеет ¥ число характерных многочленов.

Доказательство: F(x) –характеристический многочлен ЛРП: U;

G(x) – имеет старший коэффициент равный 1;

G(x)*F(x) – характеристический многочлен ЛРП: U.

Определение: характеристический многочлен наименьшей возможной степени – минимальный многочлен ЛРП: m_U(x).

Утверждение: если UÎpL(F) Þ m_U(x)½F(x); (то есть минимальный многочлен ЛРП делит любой её характерный).

Доказательство: F(x)=m_U(x)q(x)+r(x); degr(x)<degm_U(x);

F(x)U=0=[m_H(x)q(x)+r(x)]*U=q(x)*(m_H(x)U)+r(x)U=0; Þ r(x) – минимальный многочлен ЛРП U (если его поделить на С, обратную старшему коэффициенту r(x), тогда получим унитарный многочлен, а degr(x)<degm_U(x)) – противоречие.

Следствие: множество всех характерных многочленов ЛРП U имеет вид: {g(x)*m_U(x)½g(x)ÎP(x); g(x) – унитарный}.

Определение: импульсная последовательность с характерным многочленом f(x): e^fÎpL(f) – последовательность принадлежащая pL(f) с начальным вектором: (0, ….., 0, 1)=e_m-1;

Теорема: для любого HÎpL(f) $! j_U(x), degj_U(x)<m: U=j_U(x)*e^f;

Доказательство:

1. по теореме: {e^f, xe^f, …, x^m-1e^f} – базис pL(f) Þ

$! (j₀, j₁, …, j_m-1): U=j₀e^f+j₁xe^f+…+j_m-1x^m-1e^f=(j₀+j₁x+…+j_m-1x^m-1)e^f=j_U(x)*e^f; degj_U(x)<m;

Ч.Т.Д.

Определение: многочлен j_U(x) из Т – генератор плоскости U.

Следствие1: pL(f)={j(x)*e^f, j(x)ÎP[x], degj(x)<m} – другое описание множества всех ЛРП

над Р с характерным многочленом f(x).

Следствие2: j_U(x)=U(0)x^m-1+

Теорема: как найти минимальный многочлен ЛРП по её характерному:

1. пусть UÎpL(f) Þ

2. пусть V=H(x)*U Þ

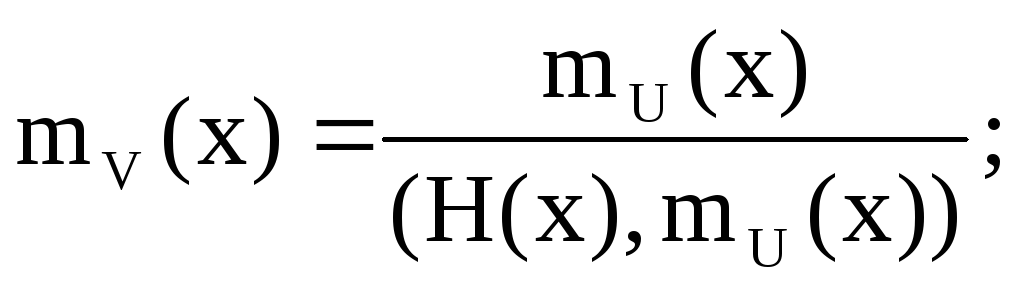
Доказательство: 2.

Þ характеристический многочлен для V и

0=m_V(x)*V= m_V(x)*H(x)*U Þ m_U(x)½H(x)*m_V(x) Þ d(x)m_U(x)=H(x)*m_V(x);

многочлен и U½m_V(x) Þ

1. заметим, что

пусть по определению;

знак с номером S последовательности равен 1, а по определению все знаки равны 0 – противоречие: то есть deg<degf(x)=m – ошибочно

Þ минимальный многочлен импульсной последовательности: deg=m;

½f(x) (оба унитарные и одной степени m) Þ =f(x);

U=j_U(x)*e^f; Þ

Ч.Т.Д.

Определение: аннулятор последовательности: A_nnU={g(x)ÎP[x]½g(x)*U=0}.

Теорема: пусть UÎpL(f) Þ A_nnU={g(x)ÎP[x]½F(x)½g(x)*j_U(x)}

Доказательство: U=j_U(x)e^f; g(x)U=g(x)* j_U(x)e^f; Þ g(x)U=0 Û g(x)j_U(x)e^f=0 Û

Ч.Т.Д.

Пример: Р={0, 1, q, 1+q}; q²+q+1=0 – определяющее соотношение. Найти генератор и т.п.

Соотношения между семействами рекуррент.

1. pL(G)ÌpL(F) Û G(x)½F(x);

2. L(G)ÇL(F)=L((G,F));

3. L(G)+L(F)=L([G,F]);

4. (F(x),G(X))= Þ L(F*G)=L(F)+L(G);

При этом представление каждой рекурренты из семейства L(F*G) в виде суммы рекуррент из семейств L(F), L(G) – однозначно.

Доказательства: 1. “Ü”F(x)=G(x)*H(x); " UÎL(G) Û G(x)*U; ½*H(x)

H(x)G(x)*U=0; F(x) Þ F(x)*U=0 Û UÎL(F)

Ч.Т.Д.

1. в одну сторону “É”:

   (G,F)½G Þ L((G,F))ÎL(G);

   (G,F)½F Þ L((G,F))ÎL(F);

   тогда L((G,F))ÌL(G)ÇL(F);

   в другую сторону “Ì”:

   пусть UÎL(F)ÇL(G); Þ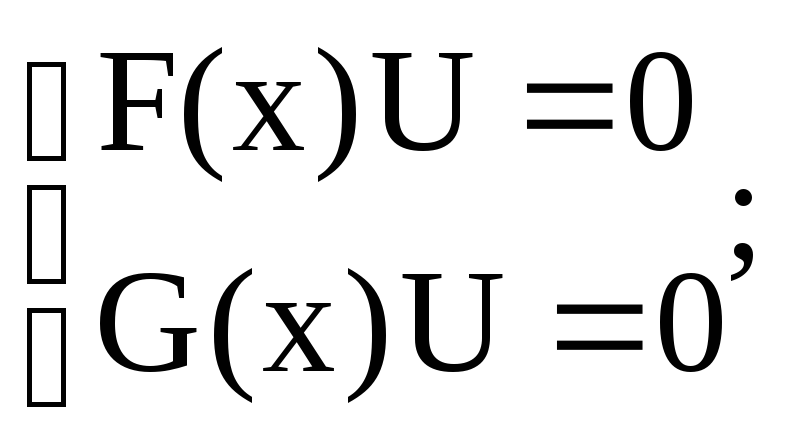(A(x)F(x)U=B(x)G(x)U=0)

   пусть A(x)F(x)+B(x)G(x)=(G,F); Þ (A(x)F(x)+B(x)G(x))*U=0; (G,F)*U=0 Û UÎL((G,F)), а так как “Ì ” и “É” то, “=”. Ч.Т.Д.

2. “Ì ”

   G(x)½[G,F] Þ L(G)ÌL[GF];

   F(x)½[G,F] Þ L(F)ÌL[GF] Þ L(G)+L(F)ÌL[GF];

   “É” : L(G)+L(F)ÉL[GF] - ?

   [GF]=F(x)*G₁(x); G₁(x)½G(x);

   

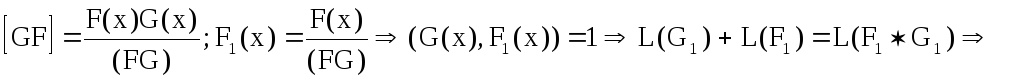
   UÎL([GF]); U=[A(x)F₁(x)+B(x)G₁(x)]*U;

   U=A(x)F₁(x)U+B(x)G₁(x)U: A(x)F₁(x)G(x)U=0 & B(x)F(x)G₁(x)U=0. Ч.Т.Д.

3. A(x)F(x)+B(x)G(x)=1;

пусть UÎL(FG); U=[A(x)F(x)+B(x)G(x)]U; Þ U=A(x)F(x)U+B(x)G(x)U Þ

A(x)F(x)UÎL(G) Þ G(x)A(x)F(x)U=A(x)(G(x)*F(x))U=0 Þ L(FG)ÌL(F)+L(G);

аналогично для B(x)G(x)UÎL(F), то есть “É”.

“Ì ” показывается как в 3:

L(F)ÌL(FG);

L(G)ÌL(FG) Þ L(F)+L(G)ÌL(FG);

Однозначность: пусть _U=V₁+W₁; V₁V₂ÎL(F);

U=V₂+W₂; W₁W₂ÎL(G);

0=(V₁-V₂)+(W₁-W₂); ½*F(x)

0=F(x)(V₁-V₂)+F(x)(W₁-W₂);

0=F(x)(W₁-W₂); ½*A(x)

0=F(x)A(x)(W₁-W₂);

0=(1-B(x)G(x))(W₁-W₂);

0=(W₁-W₂)-B(x)G(x)(W₁-W₂);

0=(W₁-W₂) Þ 0=(V₁-V₂) Þ W₁=W₂, V₁=V_2. Ч.Т.Д.

Способы представления ЛРП.

U: N₀®P; U(i) - ?

Замечание: (F,G)=1 Þ UÎL(F*G); $!: U=V+W, VÎL(F), WÎL(G).

Биномиальные последовательности. Биномиальный базис.

Пусть aÎP\0, биномиальная последовательность l-го порядка с корнем a - последовательность, знаки которой определяются по правилу:

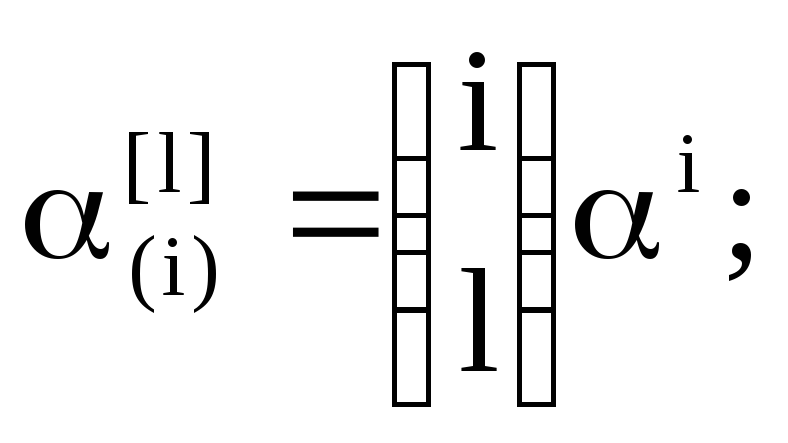
Утверждение:

Доказательство: (x-a)a^[l]=V; Þ V(i)=a^[l](i+1)-aa^[l](i)=

(x-a)a^[l]=aa^[l-1];

(x-a)²a^[l]=a²a^[l-2];

………………….;

(x-a)^la^[l]=a^la^[0], a a^[0](i)= a^l(x-a)a^[0]=0; (x-a)^l+1a^[l]=0 Þ

(x-a)^l+1 – характеристический многочлен Þ

пусть k£l,

a^l*a^[0](0)=a^l¹0 – противоречие.

Теорема: пусть рекуррентное семейство Þ a^[0], a^[1], …, a^[l] – биномиальная последовательности – образуют базис множества.

Доказательство: 1. a^[j]ÌL((x-a)^l+1); j£ l – из утверждения­.

2. покажем, что это базис:

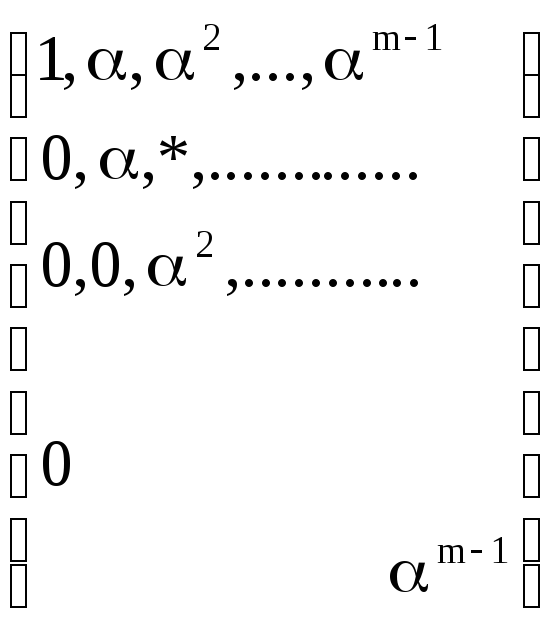; D=1*a*a²…..*a^m-1¹0 Þ базис. Ч.Т.Д.

Теорема: пусть F(x) раскладывается над Р на линейные множители:

последовательности: -образуют базис множества рекуррент pL(F).