8.2.3. Поворот гусеничного трактора з навантаженням на гаку

Для визначення основних параметрів динаміки повороту приймаємо: трактор рухається стало (j=0); радіус повороту постійний; ділянка шляху горизонтальна (α=0); буксування гусениць відсутнє; опір перекочуванню обох гусениць однаковий.

Cхема сил, які діють на трактор в даних умовах, приведена на рис. 8.8.

Поворот трактора здійснюється за рахунок різниці дотичної сили тяги на гусеницях ( Р_К2 > Р_К1 ). Під дією сили тяги на гаку полюса обертання гусениць і корпуса О₁, О₂ і О₃ зміщаються на величину Х_П назад (точки О'₁, О'₂ і О'₃ відповідно ). Величина зміщення полюсів обертання визначається за залежністю

Х_П , (8.25)

де Р_Г – сила тяги на гаку, Н;

l – відстань від середини опорної поверхні гусениць до точки прик- ладання сили тяги на гаку, м;

µ – приведений коефіцієнт опору повороту;

q_cp – середній питомий тиск гусениць на грунт, Н/м²;

b – ширина гусениці, м.

Середній питомий тиск гусениць на грунт дорівнює

q_cp = . (8.26)

Рис. 8.8. Схема сил, які діють на гусеничний трактор при повороті

з навантаженням на гаку

Із-за зміщення полюсів обертання дещо змінюється сумарний момент опору повороту (формула 8.23). Ця зміна враховується поправочним коефіцієнтом k. Тому величина сумарного момента повороту становить

М_П = . (8.27)

Точно визначити величину коефіцієнта дуже важко. В звичайних умовах повороту трактора з навантаженням на гаку величина менша одиниці і відрізняється від неї на незначну величину. Тому при приблизних, в тому числі і навчальних, розрахунках можливо приймати k = 1. В граничному випадку, при х_д/L=1/6 та х_п/L=0,207 =0,78 (х_д – величина зміщення центра тиску гусеничного трактора відносно середини опорної поверхні гусениці ).

Результуючий момент опору повороту дорівнює сумі двох моментів: сумарного момента опору повороту та момента, який утворюється від дії бокової реакції сили тяги на гаку. Величина момента дорівнює

М_РЕЗ = М_П + М_ПРг = + Р_Г tg ( l – x_п ). (8.28)

Для подолання момента опору повороту (формула 8.28) потрібен відповідний повертаючий момент. Він створюється шляхом підведення до забігаючої і відстаючої гусениць сил тяги різної величини. Величина повертаючого момента визначається із умови рівноваги трактора відносно полюсів обертання гусениць О₁ і О₂, яку записують так

Р_К2В = Р_f2B + M_П + 0,5ВР_Г + М_ПРг; (8.29)

Р_К1В = Р_f1В – М_П + 0,5ВР_Г – М_ПРг, (8.30)

де Р_f1 і P_f2 – сили опору перекочування відстаючої і забігаючої гусениць відповідно, Н.

Віднімаючи почленно від рівняння (8.29) рівняння (8.30), з урахуванням рівняння (8.28), отримаємо

В( Р_К2 – Р_К1 ) + В( Р_f2 – P_f1 ) = 2М_РЕЗ. (8.31)

Враховуючи те, що Р_f2 = Р_f1, рівняння (8.31) записуємо так

М_ПОВ = М_РЕЗ = 0,5В( Р_К2 – Р_К1 ). (8.32)

Для трактора з простим диференціальним механізмом повороту

(8.33)

де М_г – гальмівний момент;

r_к – робочий радіус зірочки.

Повертаючий момент по двигуну становить

, (8.34)

де М_кн – ведучий момент при номінальній потужності;

М_к – ведучий момент при прямолінійному русі.

Мінімальний радіус повороту при цьому R_min= 0,5В.

Для трактора з подвійним диференціальним механізмом повороту (рис.8.9)

Рис. 8.9. Схема механізма повороту з подвійним диференціалом

Рис. 8.10. Схема одинарного планетарного механізма повороту

, (8.35)

де і_диф = 2,5…3 – передавальне число подвійного диференціала, яке дорівнює

де Z_зс, Z_т, Z_о, Z_вс – число зубців, відповідно, зовнішніх сателітів, гальмівних шестерень, піввісьових шестерень, і внутрішніх сателітів.

Повертаючий момент по двигуну дорівнює

. (8.36)

Мінімальний радіус повороту R_min= 0,5В·і_диф.

У трактора з фрикційним механізмом повороту середня швидкість при повороті становить

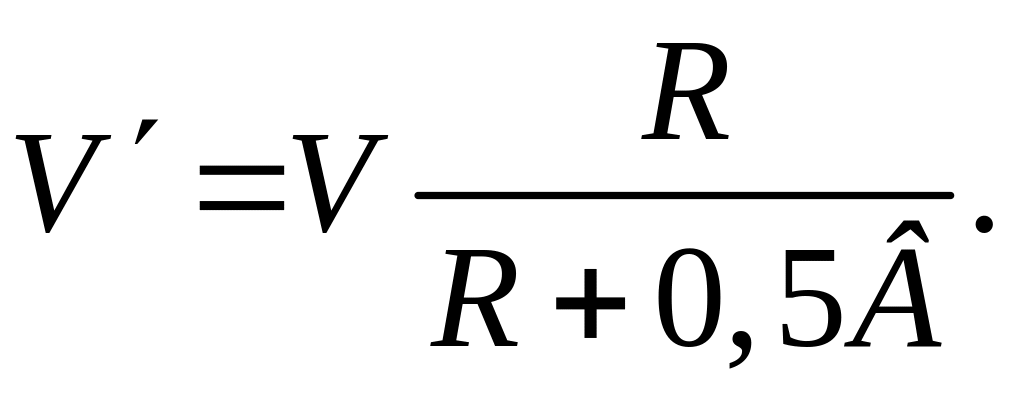
Повертаючий момент при виключеному фрикціоні дорівнює

, (8.37)

а при виключеному фрикціоні з гальмуванням відстаючої гусениці

. (8.38)

Повертаючий момент по двигуну визначається за залежністю

. (8.39)

Мінімальний радіус повороту R_min= 0,5В.

З одинарним планетарним механізмом повороту (рис. 8.10) кінематика та динаміка повороту аналогічна фрикційному механізму повороту.

При прямолінійному русі піввісьові гальма Т_о відпущені, а гальма Т_n планетарного механізму затягнуті. Передавальне число ПМП становить

, (8.40)

де Z_к і Z_с – число зубів коронної і сонячної шестерень.

Для повороту звільняють гальма Т_n планетарного механізму, для крутого повороту, крім цього, затягують піввісьове гальмо Т_о.

Характеристика повороту, це залежність моментів М_n, М_nN та М_n від радіуса R або відносного радіуса (рис 8.11).