Теоретические сведения

МОДЕЛЬ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ ДИСЦИПЛИН

ЗАМЕНЫ СТРАНИЦ В ИЕРАРХИЧЕСКОЙ ПАМЯТИ

Процесс решения на ЭВМ задач, обладающих определенной стационарностью статистических характеристик, можно описать, используя математический аппарат конечных цепей Маркова.

Будем считать, что процесс выполнения программы описывается марковской цепью первого порядка, в которой каждому из состояний ставится в соответствие одна из страниц программы.

При реализации такой программы в машинах со страничной организацией памяти широко используются алгоритмы: RAND – любая страница может с одинаковой вероятностью оказаться заменяемой; LRU – выводится из оперативной памяти страница, к которой дольше всего не было обращения; FIFO – выводится из оперативной памяти страница, которая раньше всех там оказалась. Для определенности далее рассматривается алгоритм LRU.

Полагается, что иерархическая память состоит из двух уровней: оперативной памяти и внешнего запоминающего устройства (ВЗУ). Эти уровни обозначим соответственно через u и (u+1) (см. рис. 3).

Рис. 3

ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ ОПРЕДЕЛЕНИЯ ЧИСЛА МЕЖУРОВНЕВЫХ ОБМЕНОВ

Введем следующие обозначения:

- множество страниц программы;

m – число страниц, размещающихся в верхнем уровне памяти;

x₁, x_k – соответственно начальная и конечная страницы программы;

P_ij – вероятность перехода от страницы x_i к x_j странице;

N_u^{(u+1) –} среднее число обменов между уровнями u и (u+1) в процессе реализации программы;

(N_u^(u+1)) – среднее число перезаписей страницы x_i из уровня u в уровень (u+1) в процессе реализации программы;

R_l – кратность обращений (среднее обращение к l–й странице после одной перезаписи с нижнего уровня памяти в верхний до ее удаления из верхнего уровня памяти).

Требуется определить N_u^(u+1) , если известны ; m, x, x₂, P_ij.

При решении задачи предполагается, что в системе применен алгоритм смены страниц LRU.

РЕАЛИЗАЦИЯ АЛГОРИТМА LRU

Управление замещением страниц при том или ином алгоритме осуществляется посредством определения действий операционной системы с некоторым списком страниц верхнего уровня памяти. Страницам верхнего уровня присваиваются номера от 1 до m, а всем страницам, находящимся в ОЗУ, - номера m+1. Для алгоритма LRU считается, что при обращении к странице x_l (l= ) ей присваивается номер 1 (страница x_l ставится на первое место в списке). Пусть - момент времени, в который произошло обращение к странице x_l. Тогда для любого момента времени и такого, что в интервале [ , ] не было ни одного обращения к странице x_l, ей присваивается номер по правилу:

где - число различных страниц, к каждой из которых произошло обращение в интервале времени [ , ]. Такая дисциплина перемещения страниц в списке страниц отвечает требованию алгоритма LRU: выводится из ОП страница, к которой дольше всего не было обращений. Ниже приводятся некоторые моменты перераспределения страниц в списке при m = 4:

а) страница x_l вызывается из ВЗУ. Она ставится на первое место в списке, занимающая m–е место удаляется из списка (удаляется из верхнего уровня памяти);

;

б) страница x_l вызывается с третьего места в списке. Ей присваивается первый номер, а номера страниц и увеличиваются на единицу:

в) страница x_l находится на третьем месте, и происходит обращение к странице . Страница меняется местом со страницей , а позиция страницы x_l не изменяется:

ОПРЕДЕЛЕНИЕ ЧИСЛА МЕЖУРОВНЕВЫХ ОБМЕНОВ

В ИЕРАРХИЧЕСКИХ ЗУ

Для определения числа межуровневых обменов в иерархических ЗУ можно применять два подхода:

а) аналитическое решение поставленной задачи;

б) моделирование на ЭВМ процесса реализации программ.

АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ЧИСЛА МЕЖУРОВНЕВЫХ ОБМЕНОВ

Среднее число обращений к -й странице за время реализации программы можно определить как:

,

откуда

.

Тогда выражение для имеет вид

.

Для определения составим переходную матрицу Q, интерпретируя конечную страницу программы как поглощающее состояние:

.

Матрица Q описывает поведение процесса в множестве невозвратных состояний до перехода в поглощающее состояние и позволяет определять среднее число попаданий процесса в каждое из невозвратных состояний, т.е. . Для этого образуется фундаментальная матрица . Каждый элемент фундаментальной матрицы означает среднее число попаданий процесса в данное невозвратное состояние в зависимости от начального состояния. Элементы первой строки фундаментальной матрицы равны среднему числу обращений к страницам за время выполнения программы. Таким образом, есть -й элемент первой строки фундаментальной матрицы. Определение основано на анализе перемещения страницы в списке S. Это перемещение можно описать, используя метод расширения цепи Маркова. Суть метода применительно к рассматриваемой задаче сводится к тому, что исходная марковская цепь с состояниями преобразуется в новую цепь, состояниями которой являются всевозможные списки страниц верхнего уровня памяти. Эта цепь полностью характеризует поведение страниц на верхнем уровне памяти до ее удаления из верхнего уровня. Из элементов переходов между списками страниц строится матрица , для которой можно определить фундаментальную матрицу . Первый элемент первой строки этой матрицы определяет среднее число заходов в начальное состояние, т.е. кратность .

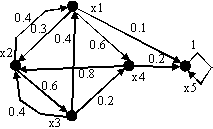
Правило составления расширенной матрицы Z поясним на примере.

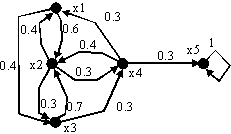
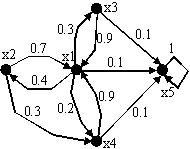
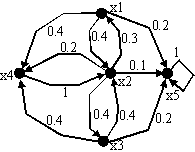
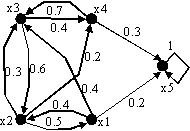
Пусть анализируемая программа состоит из 5 страниц и описывается цепью Маркова, граф которой изображен на рис. 4. Требуется построить расширенную матрицу t для второй страницы при условии, что в верхнем уровне памяти может находиться не более трех страниц (m=3). С этой целью следует рассмотреть возможные списки страниц, содержащие страницу , и переходные вероятности матрицы t с учетом положений. Страницы, стоящие в списке правее страницы , не учитываются. При определении переходных вероятностей следует помнить, что страница, с которой в данный момент работает программа, занимает первое место в списке.

Рис. 4

Так, например, список с вероятностью переходит в список (страница обращается к странице , ставится на первое место, а двигается на одну позицию вправо).

МОДЕЛИРОВАНИЕ НА ЭВМ ПРОЦЕССА РЕАЛИЗАЦИИ ПРОГРАММЫ С ЦЕЛЬЮ ОПРЕДЕЛЕНИЯ ЧИСЛА МЕЖУРОВНЕВЫХ ОБМЕНОВ

Рис. 5

Блок-схема, моделирующая процесс реализации программы, изображена на рис. 5. Исходными данными (блок 1) являются элементы переходной матрицы марковской цепи, моделирующей процесс реализации программы, размер верхнего уровня памяти и число повторений цикла решения программы.

Назначение оставшихся блоков программы пояснено на рис. 5 и не требует дополнительных комментариев. Исключение составляет блок 3, его функционирование проиллюстрируем следующим простым примером.

Пусть марковская цепь задана матрицей вероятностей перехода

На рис. 6 показаны строки матрицы в виде отрезков 1, 2, 3, 4.

Рис. 6

Допустим, что марковская цепь стартует из состояния . Выбирая случайные числа ( ) из равномерного закона распределения, будем определять исходы испытаний. Пусть первое случайное число , выданное машиной, равно 0,295. Определяем, что в качестве испытания следует принять состояние , так как случайное число попало на отрезок, соответствующий вероятности . Дальнейшая процедура: пусть =0,891, следовательно, произошел переход из состояния в состояние . Далее пусть =0,525. Значит, произошел очередной переход . Если = 0,651, то происходит переход в состояние и т. д.

Таким образом, при заданной матрице перехода Р и начальном состоянии последовательность случайных чисел 0,295; 0,891; 0,525; 0,651, … соответствует последовательности состояний марковской цепи . При другой выборке из равномерного распределения, естественно, может получиться реализация, отличная от приведенной.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

В процессе выполнения работы необходимо по заданной марковской цепи, описывающей процесс реализации программ, определить двумя методами (аналитическим и имитационным) оценки среднего числа межуровневых обменов, в которых участвовала одна из страниц программы, и сравнить полученные результаты.

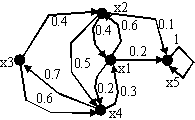
Получите у преподавателя марковскую цепь, аналогичную изображенной на рис. 4. Проведите исследования для второй страницы программы при условии, что в верхнем уровне памяти может разместиться не более m=2 страниц.

АНАЛИТИЧЕСКИЙ РАСЧЕТ

1. По заданной марковской цепи (рис. 7) постройте матрицу переходов порядка n.

2. Постройте матрицу переходов Q во множестве невозвратных состояний.

3. Постройте фундаментальную матрицу , где I – единичная матрица порядка (n-I):

.

Для расчета обратной матрицы воспользуйтесь сервисными средствами программы Mathcad.

4. Постройте расширенную матрицу Z для m=2.

5. Постройте фундаментальную матрицу с помощью процедуры, аналогичной процедуре построения матрицы L.

6. Определите среднее число обменов, в которых участвовала i -я страница. Для расчета воспользуйтесь формулой: ,

где - i-й элемент первой строки матрицы L, а - первый элемент первой строки матрицы F, построенной по матрице Z для i -й страницы.

1	2
3	4
5	6
7	8
9	10
Рис.7

МОДЕЛИРОВАНИЕ

Решите задачу определения числа межуровневых обменов с помощью имитационного эксперимента на ПЭВМ.

Вызовите программу лабораторной работы № 2 из пакета “АС ТПП” и в диалоговом режиме введите следующие данные:

• матрицу переходов ;

• количество прогонов программы МУ (МУ=I0, МУ=20, МУ=50, МУ=100, МУ=1000).

Результатом имитационного эксперимента являются:

X – среднее число обращений к i-й странице программы;

Z – среднее число обменов, в которой участвовала i-я страница.

СОДЕРЖАНИЕ ОТЧЕТА

1. Краткое описание модели управления технологическим процессом и методика расчета среднего числа межуровневых обменов.

2. Расчет величины .

3. Краткое описание моделирующей программы.

4. Листинг результатов моделирования.

5. Анализ и сравнение результатов.