- 44 -

Лабораторная работа № 1 Исследование модели нестационарного технологического процесса методом взвешенной рекурсивной регрессии

НАЗНАЧЕНИЕ И ЦЕЛЬ РАБОТЫ

Целью работы является ознакомление с методикой и алгоритмами оценки параметров нестационарных процессов по методу взвешенной рекурсивной регрессии автоматизации таких процессов.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

В современной промышленности существует большое количество технологических операций, конечный продукт которых оценивается одним или несколькими количественными показателями, причем эти показатели могут колебаться случайным образом от изделия к изделию, от партии к партии и т.д., так как они зависят от большого числа случайных факторов, таких например, как температура, давление, количество сырья, колебания технологических режимов, настройка станков и т.д.

Для любых задач управления такими технологическими операциями или объектами необходимо исследование влияния некоторых переменных на остальные и, в особенности на показатели качества конечного продукта. Таким влиянием может быть, конечно, простая функциональная связь между переменными, однако во многих физических процессах это скорее исключение, чем правило. Часто, по-видимому, существует функциональная связь, которая слишком сложна для описания в простых терминах. В таком случае мы можем стремиться подобрать аппроксимацию этой функциональной связи с помощью некоторой простой математической функции (скажем, такой, как полином) и аппроксимировать "истинную" функцию в некоторой ограниченной области изменения этих переменных.

Воспользуемся одним общеизвестным частным методом получения математической зависимости [1]. Этот метод исходит из предположения о том, что имеет место определенный тип линейной зависимости относительно неизвестных параметров. Простейшим примером этой процедуры является подбор прямой по парам наблюдений (Х₁, Y₁), (Х₂,Y₂),..., (Х_n,Y_n) над переменными Х и Y. Будем называть переменную Х независимой, т.е. такой, для которой можно устанавливать желаемые значения (например, начальную температуру) либо ее можно наблюдать, но не управлять ей (например, атмосферная влажность). В результате изменений, прошедших с независимой переменной, произведенных намеренно или случайно, происходит изменение зависимой переменной (например, чистота конечного химического продукта). Разделение на зависимые и независимые переменные является, конечно, чисто условным и зависит от наших целей.

Предположим, что мы хотим узнать, как изменения одной переменной влияют на другую и с этой целью проводим эксперимент. Если мы теперь установим связь зависимой случайной величины Х₂ и независимой Х₁ (или наоборот), то уравнение связи Х₂ с Х₁ обычно называется уравнением регрессии.

Рассмотрим, как такое уравнение можно получить методом наименьших квадратов (МНК). Предположим, что линия регрессии переменной Х₂, которую мы для удобства обозначим через Y от переменной Х₁, которую обозначим через Х, имеет вид . Тогда мы можем записать линейную модель

Y= , (1)

где  есть отклонение действительного значения Y от линии регрессии. Уравнение (1) отражает модель, которую мы предполагаем, т.е. предварительно допускаем ее правильность.

В уравнении (1) __и неизвестны, причем  меняется от наблюдения к наблюдению, а _и _- постоянны. Хотя мы не можем найти _и _точно, однако мы можем использовать информацию, содержащуюся в n наблюдениях: (X₁, Y₁), (X₂, Y₂),...(X_n, Y_n). Эта информация может быть использована для получения оценок b₀ и b₁ параметров _и _. Можно записать это в таком виде

, (2)

где есть предсказанное значение y, когда b₀ и b₁ определены. Уравнение (1) можно записать также в виде

y_i=_ _x_i + _i , . (3)

Следовательно, сумма квадратов отклонений от линии регрессии есть

. (4)

Будем подбирать значения оценок b₀ и b₁ так, чтобы их подстановка вместо _и _в уравнение (4) давала минимальное значение S. Можно определить b₀ и b₁ путем дифференцирования уравнения (4) сначала по _затем по _ и путем приравнивания результатов к нулю.

(5)

так что для оценок b₀ и b₁ имеем

(6)

где при приравнивании выражений (5) к нулю мы подставили b₀ и b₁ вместо

_и _ Из (6) имеем

(7)

или

(8)

Уравнения (8) называются нормальными. Их решение относительно b₁ дает

, (9)

где .

Решения уравнений (8) для b₀ дает

. (10)

Обозначив , получим

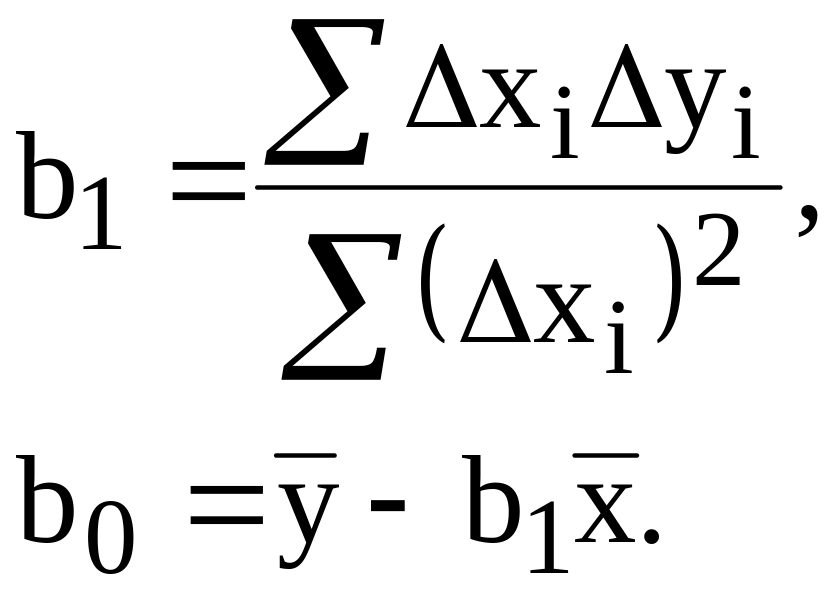(11)

Подставив (11) в (2), получим оцениваемое уравнение регрессии

. (12)

Линейная модель в общем случае может содержать и несколько независимых переменных x₁, x₂, ... , x_n и иметь вид

, (13)

или в матричной форме

Y=X +, (14)

где Y - (n  1) - вектор наблюдений,

X - (n  m) - заданная матрица,

 - (n  1) - вектор ошибок,

 - (n  1) - вектор параметров.

Нормальные уравнения в этом случае записываются в виде

(X^тX)b=X^тY, (15)

где (Т)- символ транспонирования матрицы.

Решение нормальных уравнений может быть записано в виде

b=(X^тX)^-1 X^тY, (16)

где (-1)- символ обращения матриц.

Проведенная процедура нахождения оценок по методу наименьших квадратов может быть использована тогда, когда коэффициенты __..., _m в (13) постоянны.

Однако для технологических объектов часто имеет место дрейф параметров _i, так что для целей управления необходимо решать систему нормальных уравнений (15) снова и снова, набирая новые данные и отбрасывая старые. Таким образом, процесс управления требует "свежих" оценок b_j, характеризующих состояние объекта в момент времени, возможно более близкий к настоящему, текущему моменту времени.

Объекты, коэффициенты _i которых изменяются, относятся к классу нестационарных объектов. Для таких объектов необходимо проводить текущий регрессионный анализ, заключающийся в нахождении оценок b_{i ,} которые еще не успели "устареть" для целей управления.

Однако решение системы нормальных уравнений (15) чрезвычайно трудоемко. Это приводит к тому, что за время решения уравнений, само решение может либо "устареть" для целей управления, либо требовать больших затрат оборудования. Поэтому созданы методы текущего регрессионного анализа, которые основаны на итеративном принципе. Ниже излагается один из таких методов. Этот метод является одной из разновидностей метода взвешенной рекурсивной регрессии. Суть метода состоит в следующем.

Поделив в формуле (9) числитель и знаменатель на n, получим

(17)

Так как имеют место соотношения

,

,

то

(18)

Обозначим штрихом новые расчетные значения величин, найденные при поступлении новых данных. Для расчета средних значений переменных примем экспоненциальное сглаживание. Пусть - среднее значение, полученное на основе прошлых данных, - среднее значение, посчитанное после поступления новых данных.

Для экспоненциального сглаживания имеем

. (19)

Представим новое значение b₁ в виде

b₁= b₁+ b₁, (20)

где

, b₁= f (x,y). (21)

Так как ,

то .

Так как находим

,

.

Тогда

. (22)

Вычисляя аналогично , получаем

. (23)

Подставляя (22) и (23) в (21) и преобразуя результат, получаем окончательно

. (24)

Результат (24) может быть также представлен в виде

. (25)

Таким образом, для вычисления оценки b₁ имеем простое в вычислительном соотношении рекуррентное выражение

. (26)

Аналогичные результаты могут быть получены и для моделей, в которых на y влияет большое число факторов. Например, если искомое регрессивное уравнение в оценках есть

, (27)

то при отсутствии корреляции между переменными x₁ и x₂ имеем простые соотношения

, (28)

, (29)

позволяющие определить текущие значения оценок b₁ и b₂ при непрерывном поступлении новых данных.

ЗАДАЧИ ЛАБОРАТОРНОЙ РАБОТЫ:

1. Текущее оценивание регрессионных коэффициентов _t)_t двухфакторного нестационарного технологического объекта, описываемого уравнением

, (30)

где x₁ и x₂ – факторы, влияющие на выходную величину объекта, (t) – случайная помеха, воздействующая на выход объекта, _tи _tизменяющиеся во времени (дрейфующие) коэффициенты регрессивной модели.

2. Анализ качества управления нестационарным технологическим объектом на основе текущих оценок коэффициентов _tи _t

Модель предусматривает формирование выходной величины объекта y в соответствии с выражением (30).

Факторы x₁ и x₂ задаются от программного датчика случайных чисел, распределенных по закону равномерной плотности в некотором диапазоне, указываемом преподавателем.

В качестве законов изменения (дрейфа) коэффициентов ₁ и ₂ в работе приняты

₁(t)= ₁₀ + B₁Sin ₁t + B₁₁ t , B₁< ₁₀ (31)

₂(t)= ₂₀ + B₂Sin ₂t + B₂₂ t , B₂< ₂₀ .

Набор данных для различных условий моделирования приведен в таблице (см. стр. 8). Соответствующий вариант задается преподавателем.

Блок вычисления текущих оценок коэффициентов регрессионного уравнения реализует вычислительный алгоритм, задаваемый соотношениями (28) и (29), которые выводятся на печать.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. По указанию преподавателя ввести в ЭВМ все константы, задающие состояние объекта для вычисления коэффициентов регрессии, из таблицы исходных данных.

2. Обработать результаты эксперимента в виде графиков, на которых представить действительные кривые изменения коэффициентов ₁ и ₂ , а также их оценки b₁ и b₂ (в программе B=₁, AV=b₁; Q=₂, AE=b₂).

3. Показать в виде графиков характер изменения параметров S₁ и S₂, функции Z, ошибки прогноза переменной y(t), обусловленной искажением коэффициентов _и _, если Z = Z(S₁,S₂) = Z( ₁ - b₁, ₂ - b₂).

Библиографический список

1. Драйпер Н., Смит Г. Прикладной регрессионный анализ. - М.: Статистика, 1973.

2. Бородюк В.П., Лецкий Э.К. Математическое описание промышленных объектов. - М.: Энергия, 1971.

3. Райбман Н.С., Чадаев В.М. Адаптивные модели в системах управления. - М.: Сов. радио, 1966.

№ варианта	1	2	3	4	5	6	7	8	9	10
A(0)	1	2	3	4	5	6	7	8	9	10
A(1)	3	1	6	5	4	2	7	3	7	6
A(2)	1	0,5	2	1	0,5	0,5	1	0	2	0
A(3)	1	0	0	0	1	0,5	0	2	1	0,5
Налич. или отсут. A(4)	1	1	1	1	1	1	1	1	1	1
A(5)	1,73	1,73	1,73	1,73	1,73	1,73	1,73	1,73	1,73	1,73
A(6)	1,73	1,73	1,73	1,73	1,73	1,73	1,73	1,73	1,73	1,73
A(7)	1	1	1	1	1	1	1	1	1	1
A(8)	1	1	1	1	1	1	1	1	1	1
A(9)	200	200	500	500	300	300	400	400	500	200
A(10)	400	109	109	109	106	106	104	104	105	103
A(11)	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
A(12)	0,05	0,03	0,08	0,06	0,04	0,01	0,02	0,03	0,07	0,06
A(13)	1	1	1	1	1	1	1	1	1	1
Дис. время 	0	0	0	0	0	0	0	0	0	0
AU	1	2	3	4	5	6	7	8	9	6
AE	3	1	6	5	4	2	5	9	3	6
Дискр.период. данных V	10	10	10	10	10	10	10	10	10	10
A(16)	0	0	0	0	0	0	0	0	0	0
A(17)	0	0	0,002	0,002	0,001	0,001	0,003	0,003	0,001	0,002

A(0) – коэффициент _

A(1) – коэффициент _

A(2) – коэффициент B_

A(3) – коэффициент B_

A(5) – среднее значение входной переменной х₁( )

A(6) – среднее значение входной переменной х₂( )

A(7) – среднеквадратичное отклонение переменной х₁( ). Вводится

A(8) – среднеквадратичное отклонение переменной х₂( ). Вводится

A(9) – период изменения коэффициента _

A(10) – период изменения коэффициента _

A(11) – коэффициент 2(1-), где  - коэффициент экспоненциального сглаживания 0<<1

A(12) – коэффициент 2(1-), где  - коэффициент экспоненциального сглаживания 0<<1

AU – начальное значение оценки В₁

AE – начальное значение оценки В₂

A(16) – коэффициент B_

A(17) – коэффициент B_