Теорема Ферма. П усть функция определена и дифференцируема на интервале (a;b) и в некоторой точке x0 этого интервала принимает наибольшее или наименьшее значение. Тогда .
Доказательство:
По определению производной:
.
Пусть для определенности в точке
функция
принимает набольшее значение. Тогда
числитель
.
Рассмотрим два случая:
1)
.
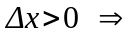
По теореме о предельном переходе в
неравенствах: предел дроби меньше нуля
.
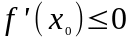2)
.
.
Ч.т.д.
Геометрический смысл теоремы Ферма:
Так как
,
то угловой коэффициент касательной
равен нулю
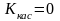
касательная параллельна оси ОХ.
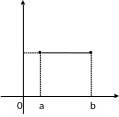
Теорема Ролля.
Пусть функция
определена и непрерывна на отрезке
[a;b] и дифференцируема на интервале
(a;b), причем на концах интервала принимает
одинаковые значения
.
Тогда существует точка с(a;b),
значения производной в которой равно
0, т.е.
.
Доказательство:
Т.к.
функция
непрерывна на отрезке [a;b], то по II-й
т. Вейерштрасса о непрерывных функциях
принимает на [a;b] наибольшее М и наименьшее
m значения. y
Возможны два случая:
1) М=m.
2)
М
m.
y
Хотя бы одна из точек, в которых функция принимает наибольшее или наименьшее значения, находится внутри [a;b].
В этом случае в указанной точке выполняются условия теоремы Ферма и, следовательно, существует точка c, принадлежащая (a;b), в которой производная .
Ч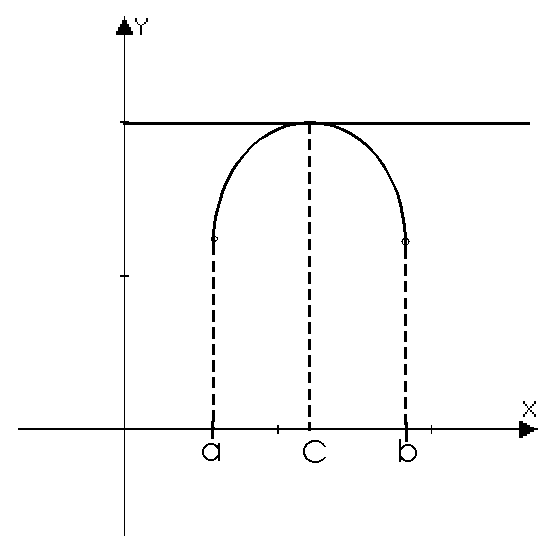
.т.д.
Геометрический смысл теоремы Ролля:
Þ Ккас=0 Þ касательная
в точке c параллельна оси ОX.
Теорема Лагранжа.
Пусть функция
определена и непрерывна на отрезке
[a;b] и дифференцируема на интервале
(a;b). Тогда существует точка c(a;b),
значение производной в которой равно
.
Доказательство:
Введем вспомогательную функцию
.
Эта функция непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций
.
Итак, для F(x) выполняются
все условия теоремы Ролля.
существует точка с(a;b)
такая, что
.
.
Ч.т.д.
Геометрический смысл теоремы Лагранжа:
.
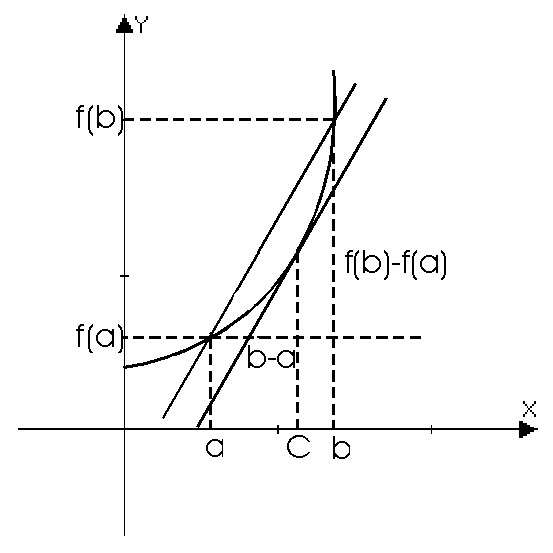Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:
.
Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].
Теорема Коши.
Пусть функции f(x) и g(x) определены и
непрерывны на отрезке [a;b] и дифференцируемы
на интервале (a;b), причем производная
функции g(x) отлична от нуля, g(x)0.
Тогда существует такая точка c(a;b),
для которой выполняется равенство:
.
Доказательство:
Рассмотрим вспомогательную функцию:
.
непрерывна и дифференцируема как сумма
непрерывных и дифференцируемых функций.
Итак, для F(x) выполняются все условия
теоремы Ролля.
существует точка с(a;b): .
;
.
.
.
Ч.т.д.
Правило Лопиталя.
Теорема.
Пусть функции f(x) и g(x) определены и
дифференцируемы в некоторой окрестности
точки x0, за исключением может быть
самой точки x0, и
,
.
Тогда если существует предел отношения
производных функций
,
то существует предел отношения самих
функций
,
причем они равны между собой, т.е.
.
Доказательство:
Доопределим f(x) и g(x) в точке x0, положив
f(x0) = g(x0) = 0.
В окрестности точки x0, т.е. на (x0,х) для функций f(x) и g(x) выполняются условия теоремы Коши. Следовательно, существует точка с(x0, х) такая, что
,
т.к. f(x0) = g(x0) = 0.
Перейдем к пределу при x
x0
с
x0:
.
Ч.т.д.
Замечание. На практике при раскрытии
неопределенности типа
можно пользоваться правилом Лопиталя
и в случаях, когда x,
x.
Для раскрытия неопределенностей типа
существует аналог правила Лопиталя,
т.е. справедливо следующее утверждение:
Теорема.
Пусть функции f(x) и g(x) непрерывны и
дифференцируемы в некоторой окрестности
точки x0, за исключением самой
точки x0, причем
.
Пусть
,
.
Тогда если существует предел отношения
производных функций
,
то существует предел отношения самих
функций
,
причем они равны между собой, т.е.
.
В дальнейшем это утверждение будем также называть правилом Лопиталя.
Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (-), (0), (1), (¥0), (00), сводя их к неопределенностям типа , .
Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида или , то его можно применить повторно.
Формулы Тейлора и Маклорена.
Теорема. Пусть функция
n раз дифференцируема в окрестности
точки x0. Тогда в этой окрестности
для функции
справедлива следующая формула Тейлора:
+
+
.
Здесь
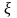некоторая точка, заключенная между
и
(
),
зависящая от
,
а
=
-
остаточный член в форме Лагранжа.
Доказательство: Обозначим через
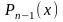многочлен
.
Ясно, что для каждого выбранного
существует такое число
,
для которого будет выполняться равенство:
.
(1)
Покажем, что это число
при уже выбранном
будет равно
при некотором
из промежутка
.
Определим функцию
.
Ясно, что
Следовательно, доказательство мы
закончим, если покажем, что в некоторой
точке
(
)
будет выполняться равенство:
.
Непосредственными вычислениями
проверяется (см. многочлен Тейлора!),
что для всех
выполняются равенства:
(2)
Число
выбрано
таким образом, чтобы выполнялось
равенство (1) и, следовательно,
.
Таким образом, для функции
на промежутке
[
]
выполняются все условия теоремы Ролля.
Следовательно, на интервале (
)
существует такая точка
,
производная функции
,
в которой равна нулю, то есть
.
Но тогда с учетом (2) теорему Ролля можно
применить к функции
на промежутке [
]
и так далее. Применяя, в конце концов,
теорему Ролля к функции
на соответствующем промежутке, получим
точку
,
для которой будет справедливо равенство
.
Утверждение доказано.
Если x0=0, то формула Тейлора превращается в формулу Маклорена:
+
Заметим, что числа n могут выбираться различными, в зависимости и от наличия у функции производных соответствующего порядка, и от необходимой точности расчетов. Например, формула Тейлора для n=4 будет иметь вид:
Разложение некоторых элементарных функций по формуле Маклорена.
1.
.
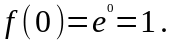
Þ
,
где
.
2.
.
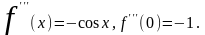
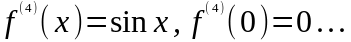
Þ
,
где
.
3.
.
,…
Þ
,
где
.
Пусть функция
определена и непрерывна на промежутке
(a;b).
Определение: Функция
называется неубывающей (невозрастающей)
на (a;b), если для любых x1<x2,
принадлежащих (a;b), выполняется
(
).
Определение: Функция
называется возрастающей (убывающей)
на (a;b), если для любых x1<x2,
принадлежащих (a;b), выполняется
(
).
Теорема 1.
Для того чтобы функция
,
дифференцируемая на (a;b), была возрастающей,
необходимо, чтобы производная на этом
промежутке была неотрицательна, т.е.
,
и достаточно, чтобы
.
Доказательство:
Необходимость.
Пусть f(x) возрастает на (a;b). Тогда для
любых
выполняется
.
Þ
Þ
.
По определению производной:
.
Достаточность.
Пусть
на (a;b). f(x) дифференцируема на (a;b). Выберем
на этом промежутке 2 точки х1; х2.
Тогда на (х1; х2) выполняется условие теоремы Лагранжа:
существует точка с (х1;
х2) такая, что
.
Þ
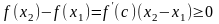(т.к.
).
.
Þ
возрастает на (a;b).
Ч.т.д.
Теорема 2.
Для того чтобы функция
,
дифференцируемая на (a;b), была убывающей,
необходимо, чтобы производная на этом
промежутке
и достаточно, чтобы
.
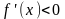