Период занятости системы m/d/1 и его продолжительность

Займемся теперь исследованием системы массового обслуживания с другой точки зрения. Заметим, что любая СМО в процессе работы последовательно проходит периоды занятости, чередующиеся с периодами простоя. Цель этого параграфа состоит в нахождении характеристик распределений длительностей периода занятости и периода простоя для системы M/G/1.

Наиболее существенными в управлении системой являются две последовательности случайных величин: последовательность моментов поступления требований и последовательность длительностей обслуживания. Введем обозначения:

– n-е требование;

– время поступления требования ;

– промежуток времени между и ;

– время обслуживания требования .

Определим теперь важный случайный процесс .

по определению – незавершенная работа системы к моменту времени t;

t – остаточное время, необходимое для освобождения системы от находящихся в ней в момент времени t требований.

Функция удачно названа незавершенной работой: она представляет собой промежуток времени, который требуется, чтобы полностью освободить систему, если после момента времени t в нее не поступают новые требования.

Обратимся теперь к рисунку 1, который показывает, каким образом период занятости чередуется с периодом простоя. Продолжительность периодов занятости обозначены , …, а продолжительность периодов простоя – , … . Требование поступает в систему в момент времени и приносит с собой работу (т. е. время, необходимое на его обслуживание) продолжительностью . Это требование застает систему свободной, поэтому его поступление завершает предыдущий период простоя и начинает новый период занятости. Предполагается, что до этого поступления система была пустой, поэтому незавершенная работа, очевидно, равна нулю.

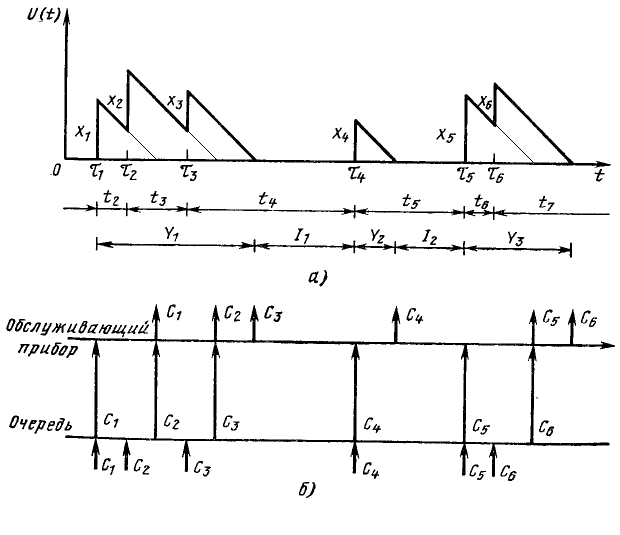
Рисунок 1. Работа СМО:

а – незавершенная работа и период занятости; б – история требований.

В момент поступления требования незавершенная работа, или задолженность системы, совершает скачок на величину , так как это время пройдет до освобождения системы, если не поступит новое требование. С момента начинается обслуживание требования , и незавершенная работа убывает со скоростью 1с/c, т. е. функция убывает с наклоном, равным –1. Через секунд, в момент времени поступает новое требование , что приводит к новому скачку незавершенной работы на величину , равную времени обслуживания требования . Затем функция снова убывает со скоростью 1с/c, и так до тех пор, пока поступление требования не приведет к новому скачку на величину в точке . Функция продолжает убывать, пока работает обслуживающий прибор, т. е. пока в момент не завершается обслуживание всех поступивших требований и система не остается пустой. В этот момент кончается период занятости и начинается новый период простоя. Период простоя кончается в момент времени , когда поступает требование . Второй период занятости характеризуется обслуживанием только одного требования, а затем снова наступает период простоя. За третий период занятости обслуживаются два требования, и т.д.

Для наглядности на рисунке б) дано обычное изображение той же последовательности требований в системе двух осей времени. На одной из этих отмечены моменты времени поступлений, а на другой – время обслуживания требований в том же масштабе, что и на рис. а), в предположении обслуживания в порядке поступления.

Таким образом, функция представляет собой ломанную линию с вертикальными скачкам и в моменты поступления требования (величина каждого скачка равна соответствующему времени обслуживания), убывающую со скоростью 1с/c до тех пор, пока она положительна. Достигнув значения нуль, функция сохраняет его до поступления следующего требования.

Как следует из рисунка а), моменты уходов могут быть получены, если продолжить убывающие куски до пересечения с горизонтальной осью. В эти моменты обслуженные требования уходят, и начинается новое обслуживание. Подчеркнем, что это замечание относится только к дисциплине обслуживания в порядке поступления. Важно, однако, отметить, что сама функция не зависит от дисциплины обслуживания! Это утверждение будет справедливым, если прибор остается занятым, пока в системе имеются требования, и если не одно требование не покидает прибор до полного завершения его обслуживания. Такая система называется “сохраняющей работу”.

Период простоя системы

Вспомним, что

где и не зависят от n.

Нас интересуют распределения

– распределение периода простоя;

– распределение периода занятости.

Вычисление распределения периода простоя для системы M/G/1 тривиально. Заметим, что когда система выходит из периода занятости, начинается новый период простоя, который длится вплоть до поступления следующего требования. Так как процесс поступления требований не имеет последействия, то время до следующего требования распределено по пуассоновскому закону, и поэтому

.

Теперь о периоде занятости; это далеко не так просто.

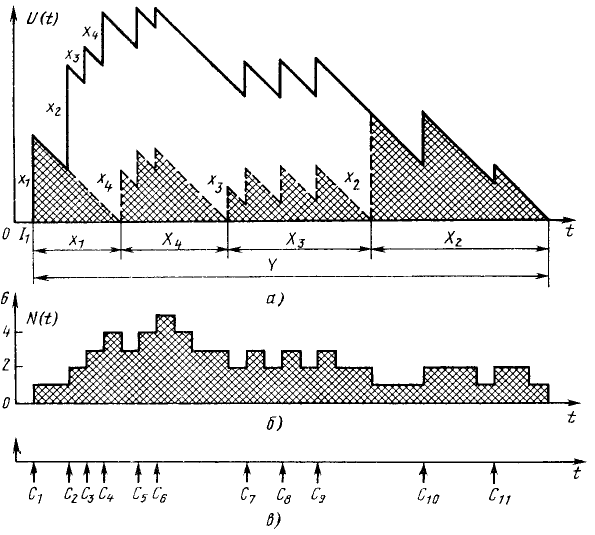
Рисунок 2. Период занятости: обслуживание в обратном порядке:

а – разложение периода занятости; б – число требований в системе;

в – история требований

Рассмотрим рисунок 2. На рис. 2а) опять рассматривается незавершенная работа . Предположим, что система свободна вплоть до момента , когда требование начинает период занятости продолжительностью Y. Время обслуживания этого требования равно . Очевидно, что это требование покинет систему в момент . За время его обслуживания в систему могут поступить другие требования, которые продлят период занятости. Как видно из рисунка, в рассматриваемом примере за время обслуживания требования поступают три других требования ( , и ). Воспользуемся прекрасной схемой, предложенной Такачем. В частности поменяем порядок обслуживания и введем дисциплину обслуживания в обратном порядке (продолжительность периода занятости не зависит от порядка обслуживания).

При уходе требования на обслуживание поступает последнее требование, в нашем случае . Кроме того, так как все последующие требования этого периода занятости должны быть обслужены раньше любого требования (кроме ), поступившего за время облуживания (в нашем примере и ), последние можно рассматривать (временно) как находящиеся вне системы. Тогда, поступая на обслуживание, требование как бы начинает новый период занятости, который назовем подпериодом занятости. Подпериод занятости, порожденный требованием , будет иметь продолжительность , точно такую же, как время обслуживания этого требования и всех новых требований, которые, поступая в систему, застают ее занятой (при этом требования и ) не учитываются. Таким образом, на рисунке 2 показан подпериод занятости, порожденный требованием , в течение которого обслуживаются в указанном порядке требования , и . В момент этот подпериод занятости кончается, и продолжается тот же обратный порядок обслуживания, применяемый теперь к возвращенному в систему требованию . Очевидно, его можно рассматривать как порождающее свой собственный подпериод занятости продолжительностью , за который в обратном порядке (а именно , , и ) обслуживаются все его “потомки”. Наконец, когда система снова оказывается пустой, возвращается требование и начинается его подпериод занятости (длиной ), которым завершается основной период занятости и в течение которого обслуживаются требования , и, наконец .

Рисунок 2а) показывает, что очертание любого подпериода занятости повторяет в точности очертание главного периода занятости над тем же промежутком времени и только сдвинуто на постоянную величину. Этот сдвиг равен суммарному времени обслуживания всех тех требований, которые поступили за время обслуживания требования и которые образуют собственные подпериоды занятости. Общее число требований в системе в любой момент времени при рассматриваемой дисциплине обслуживания показано на рисунке 2б).

Таким образом, поскольку речь идет о СМО, постольку – это строго система облуживания в обратном порядке, от начала и до конца. Однако анализ упрощается, если сосредоточить внимание на подпериодах занятости и заметить, что каждый из них статистически подобен главному периоду занятости, порожденному требованием . Это очевидно, поскольку все подпериоды занятости также, как и главный период занятости, начинаются с появления одного требования; при этом все требования независимы и имеют одно и то же распределение времени обслуживания. Каждый подпериод занятости продолжается до тех пор, пока система не сбрасывает нагрузку в том смысле, что незавершенная работа падает до нуля. Таким образом, случайные величины независимы, одинаково распределены и имеют ту же функцию распределения, что и главный период занятости Y.

Теперь наша точка зрения ясна: продолжительность Y периода занятости является суммой случайных величин, первая из которых – время обслуживания требования , а остальные описывают подпериоды занятости, каждый из которых распределен так же, как и сам период занятости. Случайная величина равна числу поступающих требований за время обслуживания требования . Отсюда получается важное соотношение

.

Обозначим функцию распределения периода занятости

.

Из предыдущего известно, что имеет функцию распределения , а – функцию распределения . Введем преобразование Лапласа для плотности распределения, связанного с Y:

.

Сведения о преобразовании Лапласа-Стилтьеса.

Пусть – функция распределения случайной величины. Тогда есть преобразование Лапласа-Стилтьеса этой функции. Например, если функция распределения характеризует экспоненциальную случайную величину , то легко получить .

Следует отличать преобразование Лапласа-Стилтьеса от обычного преобразования Лапласа . Связь между этими преобразованиями легко получить путем выполнения интегрирования по частям:

.

Тогда для экспоненциального распределения .

Обратим внимание на некоторые важные свойства преобразования.

1. Важным свойством преобразования Лапласа-Стилтьеса является то, что преобразование Лапласа-Стилтьеса суммы случайных величин равно произведению преобразований Лапласа-Стилтьеса каждой из этих величин.

2. Если есть k-й момент случайной величины относительно начала координат, то

, т. е. моменты случайной величины определяются дифференцированием в нуле (при ) соответствующее число раз преобразования Лапласа-Стилтьеса функции распределения этой величины. Первый центральный момент определяет математическое ожидание (среднее значение) случайной величины, , а второй момент нужен для нахождения дисперсии случайной величины

.

3. Вероятностный смысл преобразования Лапласа-Стилтьеса. Величина есть вероятность сложного события, состоящего в том, что случайная величина не превысит значения (сомножитель ), а кроме того, за время не произойдет ни одной “катастрофы” (сомножитель ). Параметр рассматривается как интенсивность “катастроф”. Интегрирование по всему диапазону дает . Таким образом, вероятностный смысл преобразования Лапласа-Стилтьеса состоит в том, что оно определяет вероятность того, что за время не произойдет ни одной “катастрофы”.

Воспользуемся теперь мощной техникой условных распределений, часто применяемой в теории вероятностей. Эта техника позволяет записать вероятность, связанную со сложным событием, через условные вероятности этого события при соответствующих условиях, для которых условная вероятность может быть вычислена. Если эти условия несовместимы и исчерпывающи, то безусловную вероятность находят по формуле полной вероятности как сумму произведений условных вероятностей на вероятности условий. В нашем случае будем рассматривать Y в зависимости от двух условий: длительности обслуживания требования и числа поступающих за время его обслуживания новых требований. Затем выполним следующие условные преобразования:

.

Поскольку длительности подпериодов занятости взаимно независимы, последнее равенство можно переписать в виде

.

Так как x – заданная постоянная величина, то , и, кроме того, так как подпериоды занятости распределены одинаково с соответствующим преобразованием , то

.

Поскольку представляет собой число поступающих требований за время x , то эта величина распределена по закону Пуассона со средним значением . Поэтому можно убрать условие, налагаемое на , следующим образом:

Точно так же можно убрать условие, налагаемое на , интегрируя с интегрирующей функцией , чтобы в конце концов, получить в виде

В последнем выражении легко узнать преобразование плотности распределения времени обслуживания, вычисленного для значения, стоящего в скобках в показателе степени, т. е.

. (*)

Этот главный результат дает преобразование распределения периода занятости для системы M/G/1 (при любом порядке обслуживания), выраженное функциональным уравнением (которое обычно нельзя обратить). Указанное равенство было получено в результате рассмотрения подпериодов занятости, причем эти подпериоды имеют то же распределение, что и сам период занятости.

Ввиду трудностей, связанных с обращением преобразования, найдем, что удастся, прямо из функционального уравнения; в частности, вычислим моменты периода занятости.

Определим как k-й момент распределения периода занятости. Мы намерены получить первые два момента, выраженных через моменты времени обслуживания . Имеем по определению

;

.

Из уравнения (*) непосредственно получаем

Заметим, что при также , поэтому

.

Решая относительно и учитывая, что , получаем

.

Находим, что средняя длина периода занятости для системы M/G/1 равна среднему времени, проводимому требованием в системе M/M/1, и зависит только от и .

Вычислим теперь второй момент периода занятости. Тогда

и, таким образом,

.

Решая относительно и применяя полученный результат для , получаем

,

и, окончательно,

.

Последний результат дает второй момент периода занятости. Теперь легко вычислить дисперсию периода занятости, обозначаемую через , в виде

,

или

,

где – дисперсия времени обслуживания.