Цепи Маркова

1. Определение

Рассмотрим независимые испытания, которые можно описать следующим образом. Задано множество возможных исходов (в конечном или бесконечном числе), и каждому из них соотнесена некоторая вероятность ; вероятности последовательностей исходов определяются по правилу умножения: . В теории цепей Маркова мы рассматриваем простейшее обобщение этой схемы, которое состоит в том, что для любого испытания допускается зависимость его от непосредственно предшествующего ему испытания (и только от него). С исходом не связана более фиксированная вероятность , но зато каждой паре теперь соответствует условная вероятность ; при условии, что появился в некотором испытании, вероятность появления в следующем испытании равна . Помимо нам должны быть заданы вероятности исходов в начальном испытании. Чтобы имели приписанный им смысл, вероятности последовательностей исходов, соответствующих двум, трем или четырем испытаниям, должны быть определены равенствами

и вообще

(1.1)

Здесь начальному испытанию присвоен номер нуль, так, что испытание номер один является вторым.

Определение. Последовательность испытаний с возможными исходами называется цепью Маркова, если вероятности последовательностей исходов определяются формулой (1.1) через распределение вероятностей для в начальном (или нулевом) испытании и через фиксированные условные вероятности появления при условии, что в предыдущем испытании появился .

Для приложений цепей Маркова удобнее несколько видоизмененная технология. Возможные исходы обычно называются возможными состояниями системы; вместо того, чтобы говорить, что -е испытание окончилось появлением , говорят, что -й шаг приводит к состоянию или что система попадает в на -м шаге. Наконец, называется вероятностью перехода из в . Как обычно, мы считаем, что испытания происходят через равные интервалы времени, так что номер шага служит временным параметром.

Вероятности перехода будут расположены в матрицу переходных вероятностей

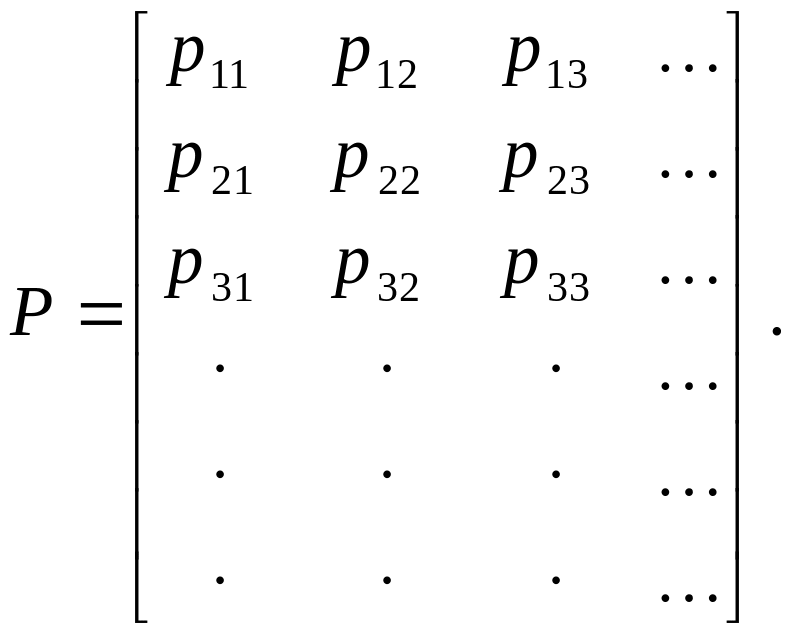(1.3)

где первый индекс означает номер строки, а второй – номер столбца. Ясно, что – квадратная матрица с неотрицательными элементами и единичными суммами по строкам. Такая матрица (конечная или бесконечная) называется стохастической матрицей. Любая стохастическая матрица может служить матрицей переходных вероятностей; вместе с нашим начальным распределением она полностью определяет цепь Маркова с состояниями .

В некоторых частных случаях бывает удобно нумеровать состояния, начиная с 0, а не с 1. Тогда к матрице следует добавить нулевые строку и столбец.

2. Пояснительные примеры

а) Когда у цепи есть только два возможных состояния , матрица переходных вероятностей с необходимостью имеет вид

.

Подобная цепь могла бы быть реализована в следующем мысленном эксперименте. Частица движется вдоль оси таким образом, что абсолютная величина ее скорости остается постоянной, но направление движения может меняться на противоположное. Говорят, что система находится в состоянии , если частица движется направо, и в состоянии , если она движется налево. Тогда – вероятность поворота, когда частица движется направо, а – вероятность поворота при движении налево.

б) Случайное блуждание с поглощающими экранами. Пусть возможными состояниями будут ; рассмотрим матрицу переходных вероятностей

.

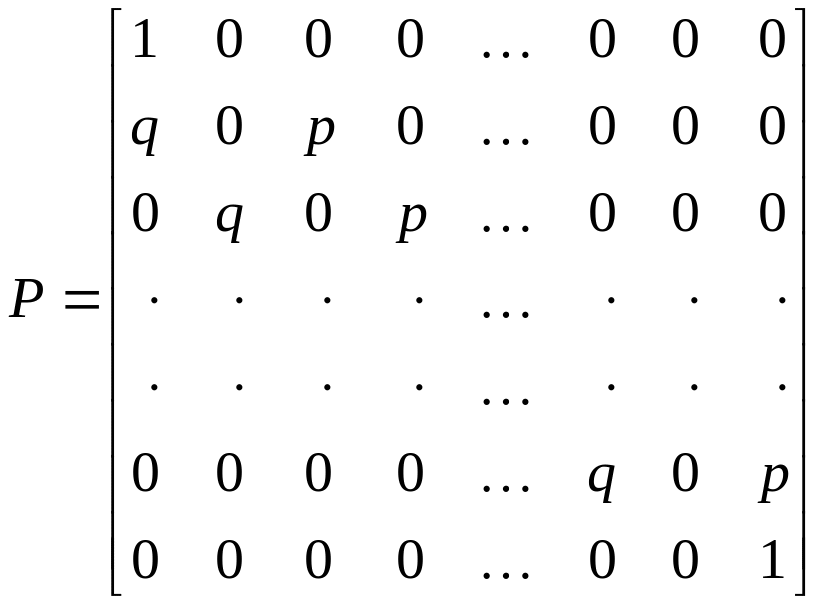Из каждого “внутреннего” состояния возможны переходы в правое и левое соседние состояния (с вероятностями и ). Однако ни из ни из невозможны переходы в какое либо иное состояние; система будет переходить из одного состояния в другое, но коль скоро будет достигнуто или система останется неизменной навсегда.

в) Отражающие экраны. Интересный вариант предыдущего примера представляет собой цепь с возможными состояниями и переходными вероятностями

.

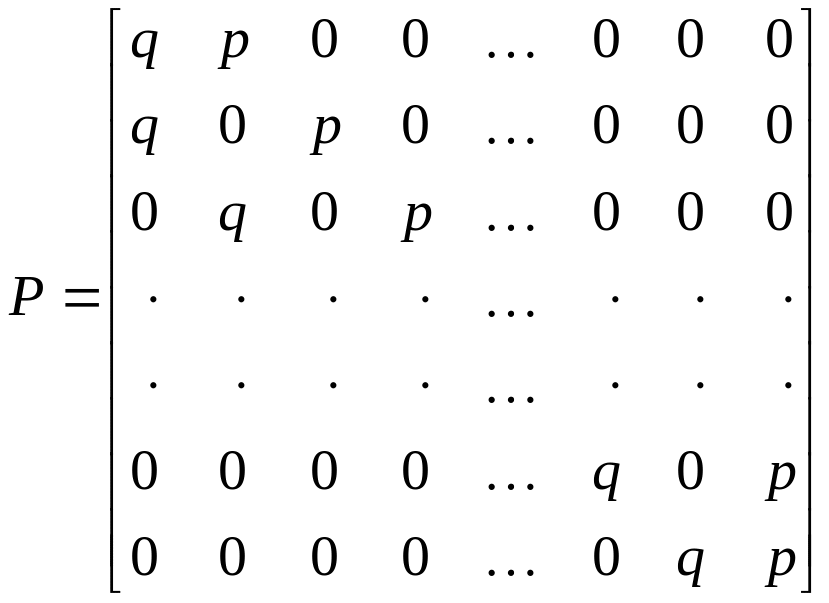Эту цепь можно интерпретировать на языке азартных игр, рассматривая двух игроков, ведущих игру с единичными ставками и с соглашением, что каждый раз, когда один из игроков проигрывает свой последний доллар, тот немедленно возвращается ему его противником, так, что игра может продолжаться бесконечно. Мы предполагаем, что игроки вместе имеют долларов, и мы говорим, что система находится в состоянии , если их капиталы равны и соответственно. Тогда переходные вероятности даются нашей матрицей .

г) Рекуррентные события и остаточные времена ожидания. Мы будем использовать цепь с набором состояний и переходными вероятностями

.

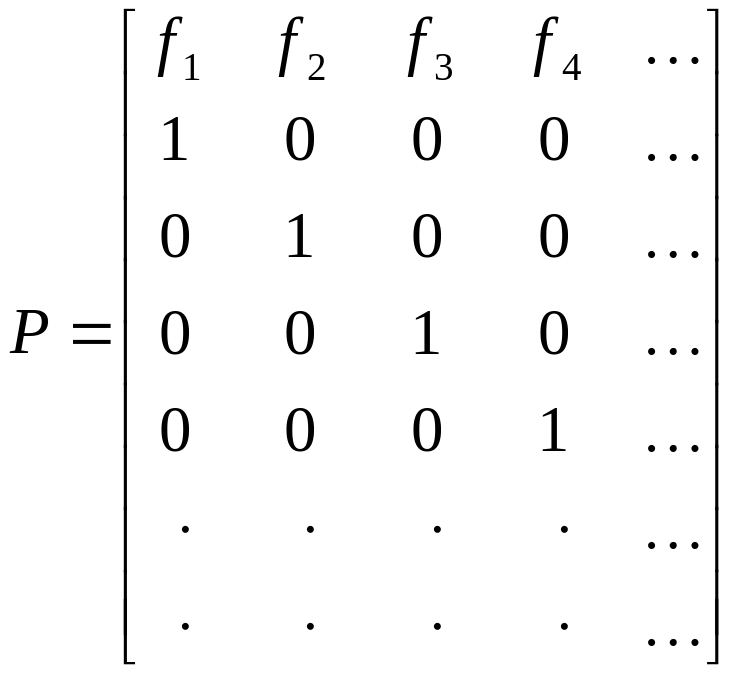Вероятности произвольны, за тем лишь исключением, что в сумме они должны давать единицу. Чтобы наглядно представить себе этот процесс, предположим, что начальным состоянием будет . Если первый шаг приводит в , то система обязана пройти последовательно через состояния и на -м шаге вернуться в , откуда процесс начнется сначала. Таким образом, последовательные возвращения в представляют из себя возвратное рекуррентное событие с распределением для времен возвращения. Состояние системы в любой момент времени определяется временем ожидания следующего прохождения через .

Данной марковской цепи соответствует модель, приведенная на рис. 1.

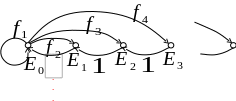
Рис. 1. Марковская модель

Например, в теории самовосстанавливающихся устройств иногда предполагается, что срок службы вновь установленного элемента зависит от выбора этого элемента, но вполне определен, коль скоро выбор уже сделан. С другой стороны, в теории массового обслуживания последовательные моменты начала обслуживания отдельных клиентов обычно соответствуют рекуррентным событиям. Предположим теперь, что имеется много типов клиентов, и для каждого из этих типов требуется обслуживание известной продолжительности. Тогда время ожидания между двумя последовательными моментами начала обслуживания определяются единственным образом с того момента, когда начинается обслуживание соответствующего клиента.

г) Другая цепь, связанная с рекуррентными событиями. Рассмотрим цепь с набором возможных состояний и переходными вероятностями

,

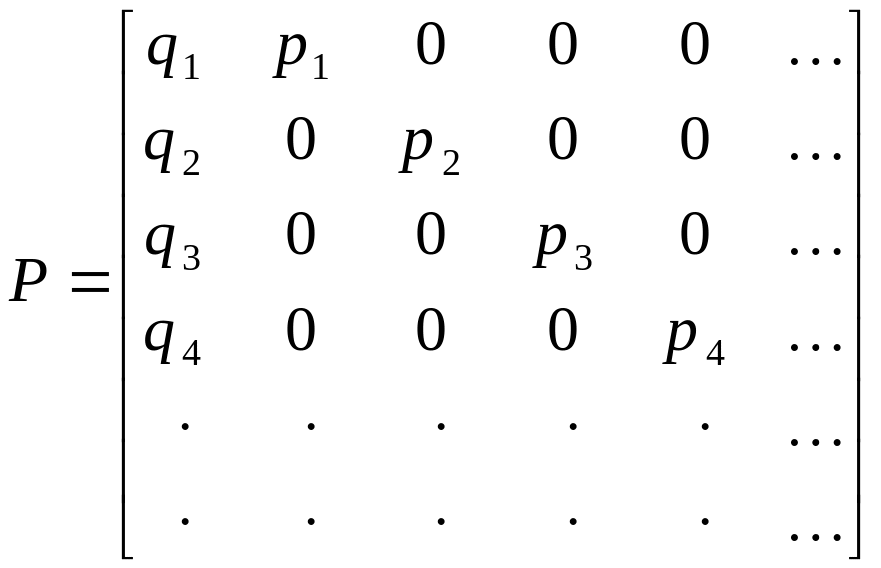где (рис. 2).

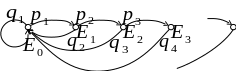
Рис. 2. Другая марковская модель

Для наглядности мы можем интерпретировать состояние как представляющее “возраст” системы. По достижении системой возраста процесс старения с вероятностью продолжается, а с вероятностью система “омолаживается”, и процесс начинается заново – с нулевого возраста. Последовательные прохождения через состояние здесь снова представляют рекуррентное событие, и вероятность того, что время возвращения равно , дается произведением . Можно подобрать так, чтобы получить заданное распределение для времен возвращения; достаточно положить , затем и т.д. В общем виде

. (2.5)

Таким образом, произвольное рекуррентное событие с распределением времен возвращения соответствует цепи Маркова с матрицей , определяемой вероятностями (2.5). После -го испытания система окажется в состоянии тогда и только тогда, когда последним испытанием, при котором произошло событие , было испытание с номером (здесь ). Номер этого состояния часто называется “затраченным временем ожидания”.

д) Серии успехов. В качестве частного случая предыдущего примера рассмотрим последовательность испытаний Бернулли и условимся, что при -м испытании система будет в состоянии , если последняя неудача наблюдалась при испытании с номером . Здесь , и считается, что нулевое испытание привело к неудаче. Иначе говоря, индекс равен длине непрерывавшейся последовательности успехов, оканчивающейся -м испытанием. Переходные вероятности здесь те же, что и в предыдущем примере с и .