Задача № 4 Расчет и обоснование складских запасов на предприятии

1. Цель и задачи работы

Целью работы является ознакомление с действующими методиками расчетов производственных запасов материально-технических ресурсов (МТР) и обоснования их нормативных размеров, а также выработка навыков и умений практической работы в сфере логистики запасов МТР.

Задачами работы является проведение специальных плановых расчетов по обоснованию размера производственного запаса и его составляющих (страхового и текущего складских запасов) в зависимости от характера имеющейся информации.

2. Постановка задачи

В практике планово-экономических расчетов по обоснованию нормативов производственных запасов материально-технических ресурсов на промышленных предприятиях широко используются:

• методы теории вероятностей и математической статистики,

• методы планирования на основе анализа статистических данных за предшествующие периоды деятельности предприятия;

• оптимизация размера партии поставок для регулярно закупаемых материальных ресурсов.

Согласно представленной исходной информации (исходным данным) предлагается произвести расчет оптимального размера производственных запасов, используя вышеназванные методики, в три этапа.

Исходные данные и методические указания к проведению расчетов представляются для каждого метода в рамках соответствующего этапа.

На четвертом этапе предлагается проиллюстрировать графически взаимосвязь различных составляющих производственного запаса по данным аналитических расчетов предшествующих этапов.

2. Исходные данные, методические указания и пояснения по ходу выполнения работы

2.1. Этап 1

На данном этапе предлагается произвести расчет планового размера производственного запаса сырья на складе с применением методов теории вероятностей и математической статистики (1 час).

Необходимо определить плановый расчетный запас сырья на складе предприятия, принимая во внимание, что в рассматриваемой системе складских запасов имеет место следующее распределение доверительной вероятности осуществления объема поставки (Q_пост) и объема выдачи (Q_выд) сырья, представленное в общем виде:

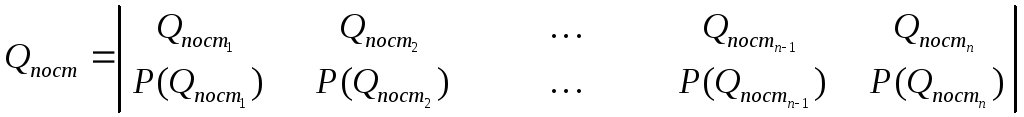(1.1)

(1.2)

где:

• P(Q_{пост i}) и P(Q_{выд j}) – соответственно величина вероятности того, что на склад прибудет Q_{пост i} количество сырья, а со склада будет выдано Q_{выд j} количество сырья.

• n – количество вариантов поставок сырья разного (i) объема,

• m – количество вариантов выдачи сырья со склада разного (j) объема.

Исходная статистическая информация по различным вариантам представлена в таблицах 1.1 и 1.2.

Таблица 1.1

Объем поставки и выдачи сырья (по вариантам для студентов)

№ варианта (для студента)	Объем поставки в тоннах				Объем выдачи в тоннах
	Qпост1	Qпост2	Qпост3	Qпост4	Qвыд1	Qвыд2	Qвыд3
1	2	3	4	5	6	7	8
1	100	150	200	240	80	120	180
2	85	125	160	210	90	125	150
3	60	100	140	180	110	150	160
4	120	145	185	220	120	150	180
1	2	3	4	5	6	7	8
Окончание табл. 1.1.
№ варианта (для студента)	Объем поставки в тоннах				Объем выдачи в тоннах
	Qпост1	Qпост2	Qпост3	Qпост4	Qвыд1	Qвыд2	Qвыд3
5	110	140	175	205	130	160	190
6	90	115	135	175	100	150	175
7	105	135	165	190	90	120	150
8	150	250	350	400	120	200	300
9	125	130	225	275	130	160	200
10	115	130	160	185	100	150	200
11	140	175	205	110	160	210	150
12	115	160	175	90	140	180	150
13	135	205	190	105	185	220	170
14	250	175	400	150	140	185	160
15	130	190	275	125	175	205	150
16	165	400	185	175	150	175	120
17	350	275	250	130	170	190	200
18	225	185	130	175	120	140	160
19	160	190	130	160	135	175	150
20	185	200	175	205	155	180	210

Таблица 1.2

Вероятность осуществления поставок и выдачи сырья

№ варианта	Вероятность поставки				Вероятность выдачи
	Р(QП1)	Р(QП2)	Р(QП3)	Р(QП4)	Р(QB1)	Р(QB2)	Р(QB3)
1	0,15	0,25	0,40	0,20	0,15	0,50	0,35
2	0,1	0,2	0,5	0,2	0,4	0,2	0,4
3	0,2	0,15	0,35	0,3	0,35	0,35	0,3
4	0,05	0,35	0,4	0,2	0,25	0,35	0,4
5	0,25	0,25	0,25	0,25	0,45	0,25	0,3
6	0,2	0,2	0,3	0,3	0,4	0,4	0,2
7	0,35	0,35	0,1	0,2	0,15	0,6	0,25
8	0,4	0,2	0,2	0,2	0,25	0,25	0,5
9	0,25	0,15	0,4	0,2	0,3	0,2	0,5
10	0,35	0,25	0,2	0,2	0,3	0,3	0,4
11	0.25	0,2	0,35	0,2	0,25	0,35	0,4
12	0,35	0,35	0,1	0,2	0,45	0,25	0,3
13	0,15	0,25	0,3	0,3	0,25	0,55	0,2
14	0,4	0,2	0,2	0,2	0,15	0,6	0,25
15	0,2	0,2	0,3	0,3	0,15	0,50	0,35
16	0,15	0,45	0,2	0,2	0,3	0,35	0,35
17	0,15	0,25	0,3	0,3	0,15	0,6	0,25
18	0,2	0,2	0,2	0,4	0,25	0,3	0,45
19	0,25	0,15	0,4	0,2	0,35	0,35	0,3
20	0,25	0,25	0,25	0,25	0,5	0,1	0,4

Доверительную вероятность (надежность оценки) определения расчетной величины запасов сырья рекомендуется принимать по вариантам согласно данных таблицы 1.3.

Таблица 1.3

Доверительная вероятность (надежность оценки) событий

№ варианта (для студента)	Доверительная вероятность
1, 6	0,950
2, 7	0,945
3, 8	0,964
4, 9	0,955
5, 10	0,935
11,16	0,945
12, 17	0,954
13, 18	0,975
14, 19	0,969
15, 20	0,962

Дальнейшее решение задачи рекомендуется проводить, используя рекомендуемые формулы в следующей последовательности:

1. Расчет страхового запаса:

(1.3)

2. Расчет размера производственного запаса при различных сочетаниях грузопотоков (объемов “i”поставки и “j”выдачи сырья):

(1.4)

3. Расчет вероятности наличия производственного запаса при различных сочетаниях грузопотоков (объемов “i”поставки и “j”выдачи сырья):

(1.5)

Примеры расчета запасов и вероятности их наличия для некоторых сочетаний (для варианта 1):

1. З_стр = 180 – 100 = 80 тонн

2. для Q_П1 и Q_B1 : З₁₁ = 80 + 100- 80 = 100 тонн

Р (З₁₁ = 100) = 0,150,15 = 0,0225

3) для Q_П1 и Q_B3 : З₁₃ = 80 + 100 – 180 = 0 тонн

Р (З₁₃ =0) = 0,150,35 = 0,0525

4) для Q_П3 и Q_B3 : З₃₃ = 80 + 200 - 180 = 100 тонн

Р (З₃₃ =100) = 0,40,35 = 0,14

5) для Q_П4 и Q_B3 : З₄₃ = 80 +240 - 180 = 140 тонн

Р (З₄₃ =140) = 0,20,35 = 0,070

Таким образом, должно быть определено 12 сочетаний грузопотоков на входе и выходе склада сырья (n*m =4*3=12).

4. Проверка нормированного условия, по которому сумма вероятностей всех событий, образующих полную группу (их получилось 12), должна быть равна 1.

(1.6)

Для рассматриваемого примера:

0,0225 + 0,075 + 0,0525 + 0,0375 + 0,125 + 0,0875 + 0,06 + 0,2 + 0,14 + 0,03 + 0,1 + 0,07 = 1,00

Таким образом, проверка подтвердила правильность расчетов.

5. Формирование сводной таблицы 1.4 для определения зависимости производственного уровня запасов сырья на складе от вероятности данного события (для всех 12 комбинаций).

Таблица 1.4

Зависимость наличия текущего уровня запасов от вероятности данного события (для варианта 1)

Производственный запас (Зпр), тонн	0	50	60	100
Вероятность наличия запаса Р (Зпр)	0,0525	0,0875	0,075	0,0225	0,14	0,07
Производственный запас (Зпр), тонн	110	150	160	200		240
Вероятность наличия запаса Р (Зпр)	0,125	0,00375	0,2	0,06	0,10	0,03

6. Построение интегральной функции распределения (накопленной вероятности) от меньших запасов к большим запасам по всей амплитуде изменений (таблица 1.5).

Таблица 1.5

Расчет функции накопленной вероятности

Производственный запас (Зпр), тонн	0	50	60	100	110
Функция накопленной вероятности F (Зпр)	0,0525	0,14	0,215	0,4475	0,5725
Производственный запас (Зпр), тонн	150	160	200	240
Функция накопленной вероятности F (Зпр)	0,61	0,81	0,97	1,00

7. Поиск интервала накопленных вероятностей, в который попадает заданная доверительная вероятность наличия запасов (для 1-го варианта - 0,95) и соответствующего интервала для производственных складских запасов:

0,81 < P=0,95 < 0,97

160 < З^пр < 200

8. Расчет оптимальной величины складских запасов в интервале З^пр160; 200, определяя ее по формуле линейной экстраполяции:

Проверка полученного результата: оптимальная величина производственного запаса (195 тонн) находится в заданном интервале З^пр160; 200.

9. Расчет нормы страхового запаса (N_стр) по отношению к оптимальному производственному запасу:

(1.7)