
- •Оглавление
- •Базы данных/Управление данными Олейник а.Г.
- •Базы данных. Реляционная модель данных: базовые понятия. Целостность бд.
- •Транзакции в базах данных. Управление транзакциями (конфликты, блокировка, сериализация)
- •Функциональные зависимости в данных. Нормализация данных. Нормальные формы (1нф-4нф)
- •Информационные сети/сети эвм и телекоммуникаций Шишаев м.Г.
- •Основные задачи уровня канала данных в сетях эвм и методы их решения
- •Сравнительная характеристика методов коммутации: каналов, сообщений, пакетов. Коммутация в сетях атм
- •Эталонная модель взаимодействия открытых систем. Состав уровней взаимодействия. Протокол уровня и межуровневый интерфейс
- •Маршрутизация в сетях эвм, типология алгоритмов маршрутизации
- •Методы аналоговой и дискретной модуляции и мультиплексирования
- •Компьютерная графика/Компьютерная геометрия и графика Рыженко а.А.
- •Алгоритмы заливки замкнутых областей
- •Виды компьютерной графики. Цветовые модели. Кодирование цвета
- •4. Корпоративные ис Маслобоев а.В.
- •Принципы организации и функционирования управляющих информационно-вычислительных систем
- •Технологии построения распределенных вычислительных систем (rpc, com, corba)
- •Типовые компоненты информационных систем, базовые логические архитектуры ис
- •6. Методы оптимизации Македонов р.А.
- •Классификация оптимизационных задач и способов их решения
- •7. Мультимедиа технология Вицентий а.В.
- •Классификация и области применения мультимедиа приложений
- •8. Надежность, эргономика и качество асОиУ/Надежность ис Тоичкин н.А.
- •Виды резервирования систем. Постановка задачи оптимального резервирования. Подходы к решению задачи оптимального резервирования
- •Классические методы расчета надежности
- •Система показателей надежности: показатели безотказности, сохраняемости, ремонтопригодности, долговечности
- •9. Операционные системы Шишаев м.Г.
- •Основные принципы организации файловых систем unix: пространство имен; структура записи каталога; структура описателя файла (inod-а); выделение блоков
- •Понятие операционной системы (ос). Основные функции ос. Классификация ос
- •Принципы организации системы прерывания программ. Векторное прерывание. Программное управление приоритетом
- •Концепция и принципы организации виртуальной памяти. Задачи управления виртуальной памятью. Страничный обмен
- •10. Организация эвм и систем/Архитектура эвм и систем Шишаев м.Г.
- •Архитектура эвм. Программная модель процессора. Режимы адресации памяти
- •Защищенный режим работы процессоров Intel: концепция, основные понятия, техника формирования физического адреса
- •Архитектура эвм с общей шиной. Принцип действия синхронных и асинхронных шин. Примеры и характеристика шин ввода-вывода
- •12. Представление знаний в ис Фридман а.Я.
- •14. Проектирование асоиу/Проектирование ис Тоичкин н.А.
- •Понятие жизненного цикла информационной системы. Модели жизненного цикла ис
- •Структурный и объектно-ориентированный подходы к проектированию программного обеспечения
- •15. Системное по Ломов п.А.
- •Основные этапы компиляции программ
- •Способы задания формальных языков. Классификация грамматик по Хомскому
- •16. Системы искусственного интеллекта/интеллектуальные информационные системы Фридман о.В.
- •Подходы к построению систем ии (логический, структурный, эволюционный, имитационный). Архитектура и основные составные части систем ии
- •17. Теоретические основы автоматизированного управления Малыгина с.Н.
- •Понятие автоматического и автоматизированного управления. Классификация систем автоматизированного управления
- •18. Теория вероятностей, математическая статистика и случайные процессы/Вероятность и статистика Селякова с.В.
- •Основные понятия и определения теории вероятностей. Законы распределения случайной величины. Характеристики случайной величины
- •Основные понятия и определения математической статистики. Типичные задачи математической статистики. Проверка правдоподобия гипотез
- •19. Теория игр и исследование операций Степенщиков д.Г.
- •Смешанное решение матричной игры
- •20. Теория информационных процессов и систем Быстров в.В.
- •Нечеткие множества: основные понятия, базовые операции
- •Основные принципы моделирования (виды подобия), классификация моделей
- •Система (понятие, определение, классификация, большие и сложные системы)
- •21. Теория принятия решений Фридман а.Я.
- •2 Основных этапа многокритериальной оптимизации.
- •Аксиома Парето и эффективные варианты. Определение множества Парето в дискретном и непрерывном случаях
- •Количественная оценка эффективности решений: функция полезности
- •22. Технология программирования Тоичкин н.А.
- •Рекурсивные алгоритмы. Примеры рекурсивных алгоритмов
- •Анализ временной сложности (трудоемкости) алгоритмов
- •23. Численные методы/Вычислительная математика Малыгина с.Н.
- •Постановка задач аппроксимации функций одной переменной: Интерполирование алгебраическими многочленами.
- •Методы решения систем линейных алгебраических уравнений
Методы решения систем линейных алгебраических уравнений
-
План ответа:
Постановка задачи
Прямые методы (определение, примеры)
Итерационные методы (определение, понятие одношаговых и двухшаговых методов, условия окончания итераций, каноническая форма записи итерационных методов, понятие стационарных, нестационарных, явных и неявных методов, понятие матрицы перехода от n-ой итерации к (n+1)-ой, достаточное условие сходимости стационарных методов, необходимое и достаточное условие сходимости стационарных методов)
Рассмотрим задачу численного решения системы вида
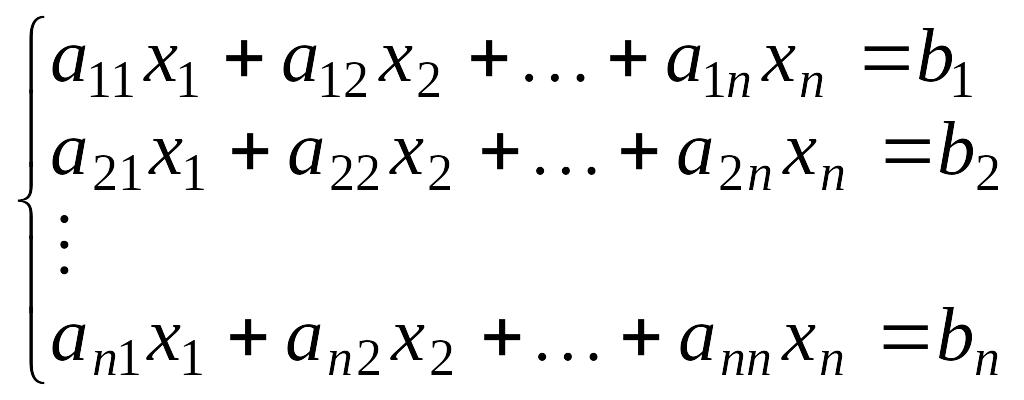 (1)
(1)В матричном виде она записывается
Ax = b, (1а)
где
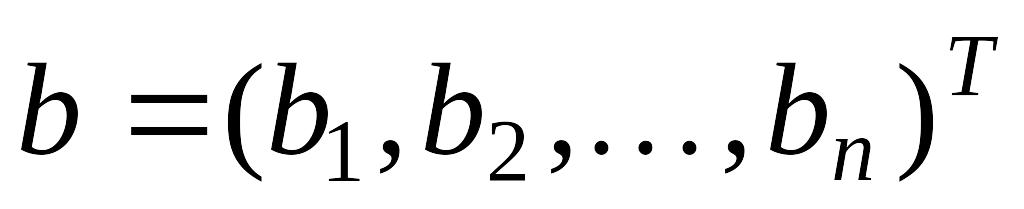 - вектор свободных членов;
- вектор свободных членов;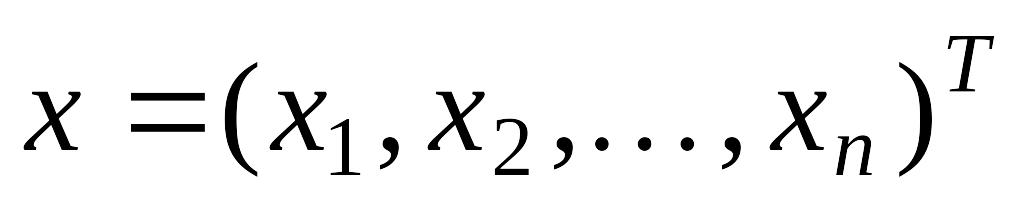 - вектор неизвестных с вещественными
координатами;
- вектор неизвестных с вещественными
координатами;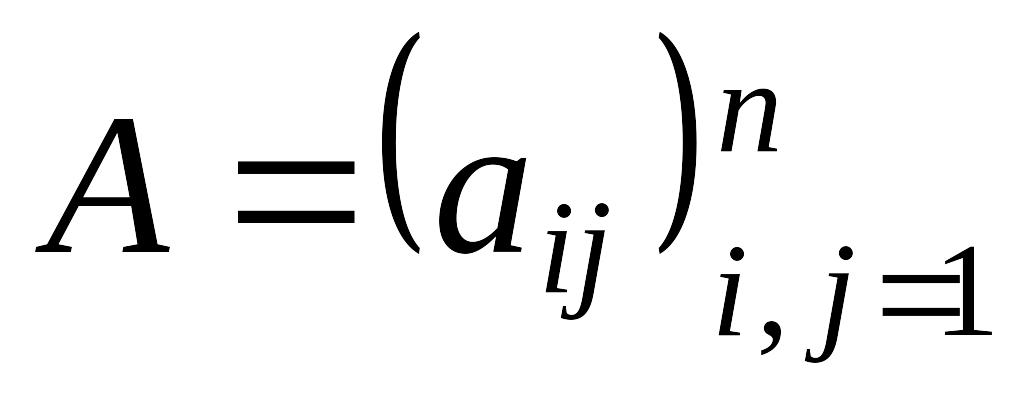 - вещественная квадратная матрица
коэффициентов системы размерности
- вещественная квадратная матрица
коэффициентов системы размерности
 .
.Будем предполагать, что определитель матрицы A отличен от нуля. Тогда для каждого вектора b система (1) имеет единственное решение.
Для решения таких систем можно использовать как прямые, так и итерационные методы.
Прямые методы позволяют за конечное число действий получить точное решение системы уравнений, если входная информация задана точно и вычисления ведутся без округления (напр., методы Гаусса, Крамера и т.п.).
Итерационный метод позволяет найти приближенное решение системы путем построения последовательности приближений (итераций), начиная с некоторого начального приближения. Само приближенное решение является результатом вычислений, полученным после конечного числа итераций.
Перейдем к общему описанию метода итераций для решения СЛАУ. Будем рассматривать систему
 (1)
(1)Для ее решения выбирается некоторое начальное приближение
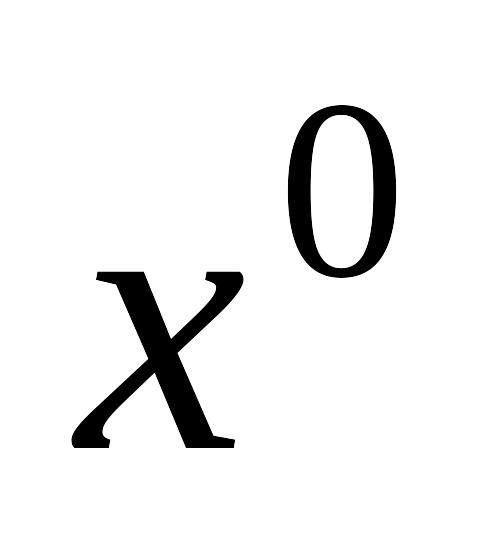 ,
и последовательно находятся приближенные
решения (итерации) уравнения (5.1).
Значение итерации
,
и последовательно находятся приближенные
решения (итерации) уравнения (5.1).
Значение итерации
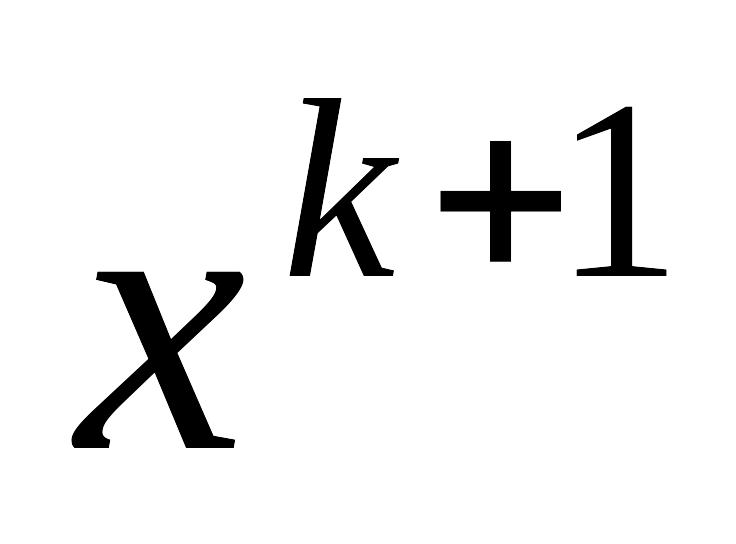 выражается через известные предыдущие
итерации
выражается через известные предыдущие
итерации
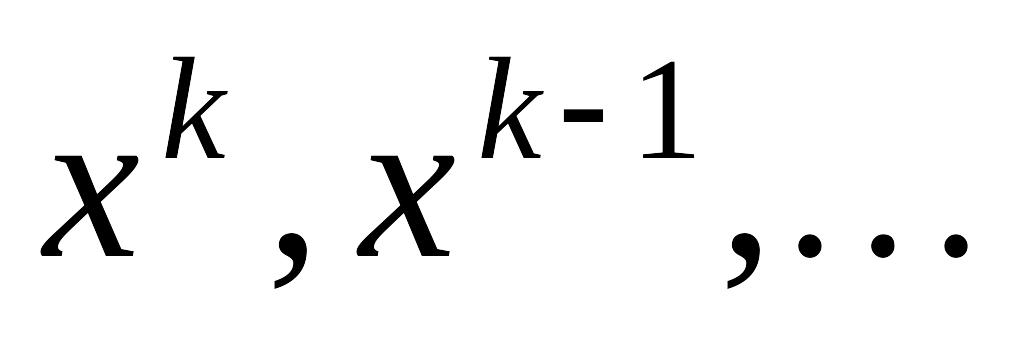 .
.В дальнейшем верхний индекс будет указывать номер итерации, т.е.
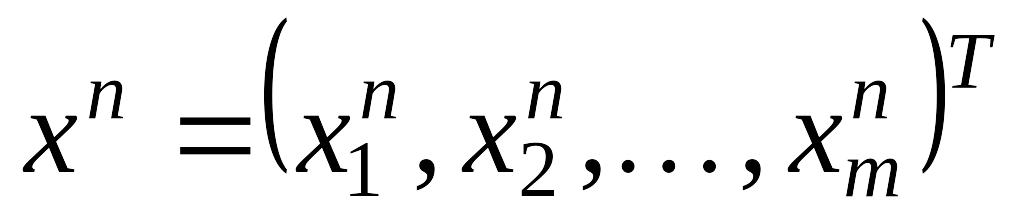 ,
где
,
где
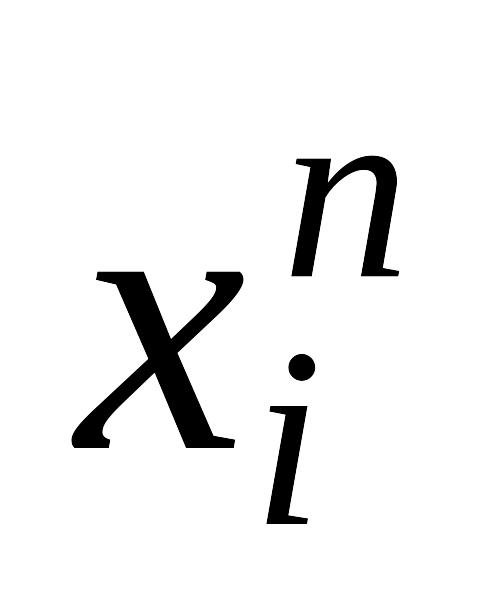 - n-ая итерация i–той
компоненты вектора x.
- n-ая итерация i–той
компоненты вектора x.Определение 1 Если при вычислении используется только одна предыдущая итерация
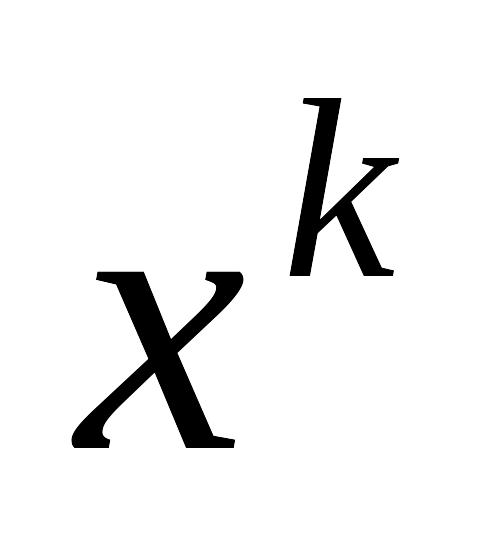 ,
то итерационный метод называют
одношаговым (или двухслойным)
методом; если же
выражается через две итерации
и
,
то итерационный метод называют
одношаговым (или двухслойным)
методом; если же
выражается через две итерации
и
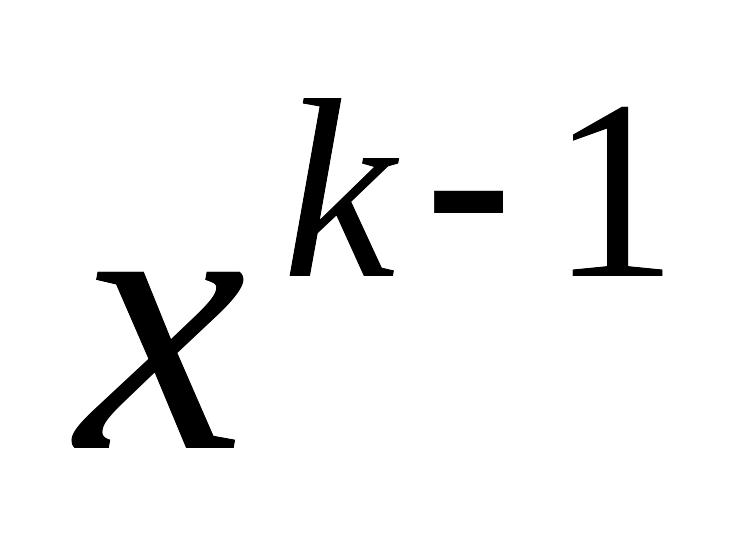 ,
то метод называют двухшаговым
(или трехслойным).
,
то метод называют двухшаговым
(или трехслойным).Окончание итераций определяется либо заданием максимального числа итераций
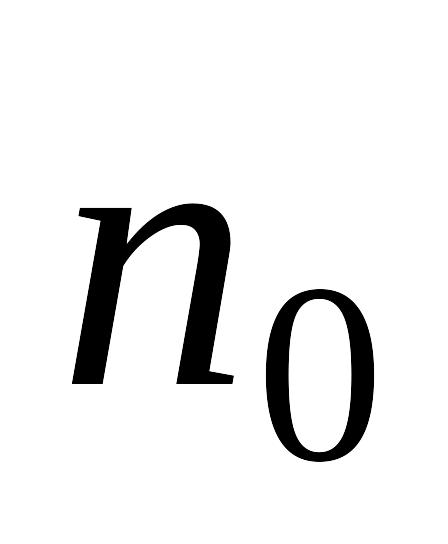 ,
либо условием
,
либо условием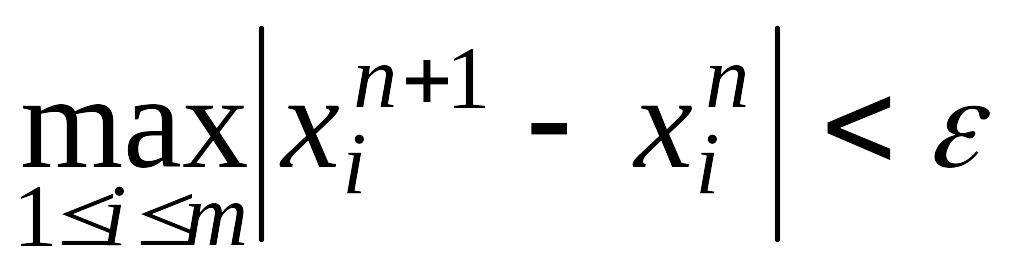 , (2)
, (2)где > 0 – заданное число.
Определение 2. Канонической формой одношагового итерационного метода решения системы вида (5.1) называется его запись в виде
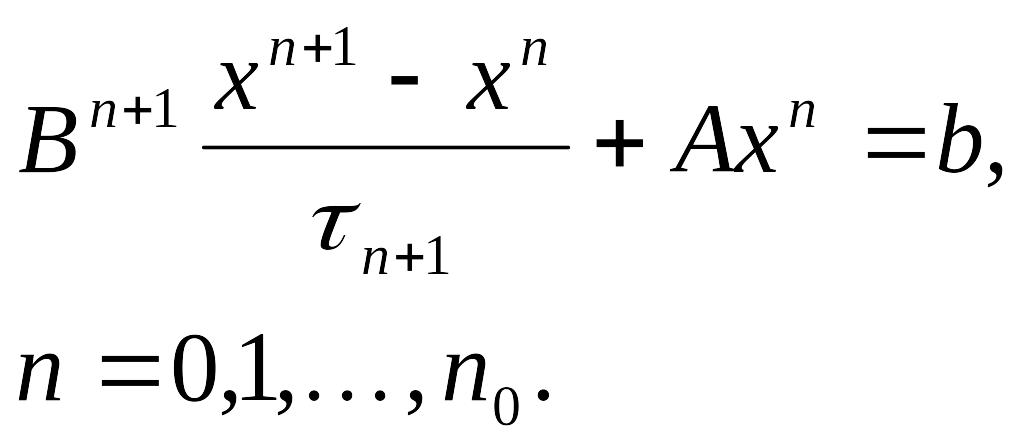 (3)
(3)Здесь
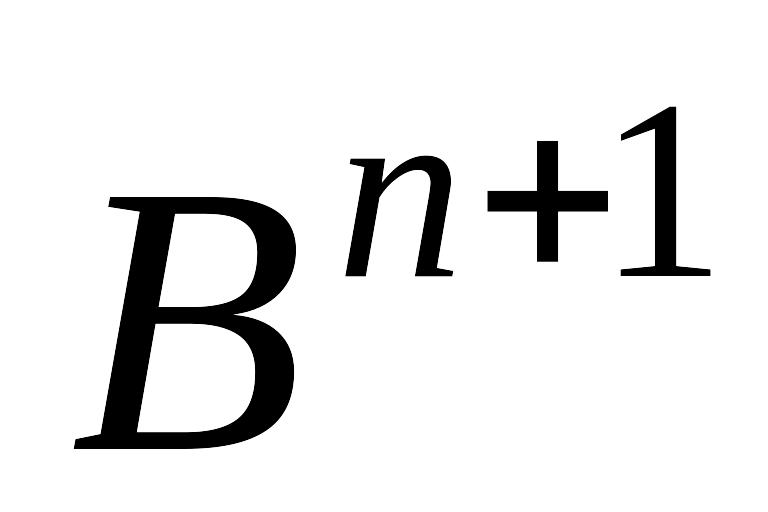 - матрица, задающая тот или иной
итерационный метод,
- матрица, задающая тот или иной
итерационный метод,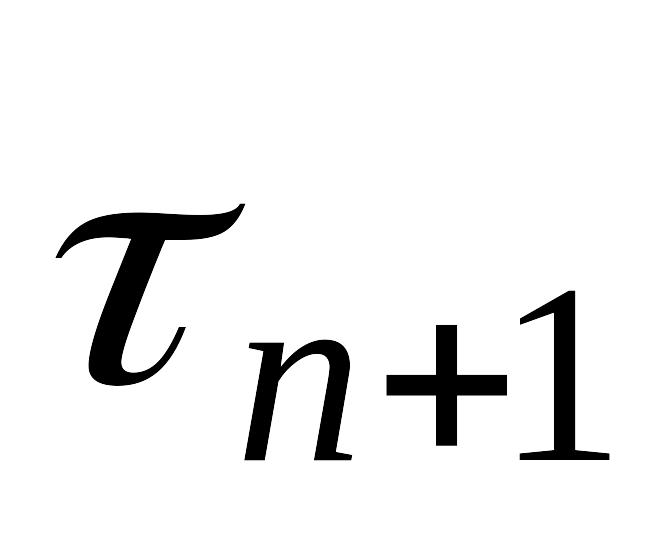 - итерационный параметр,
- итерационный параметр,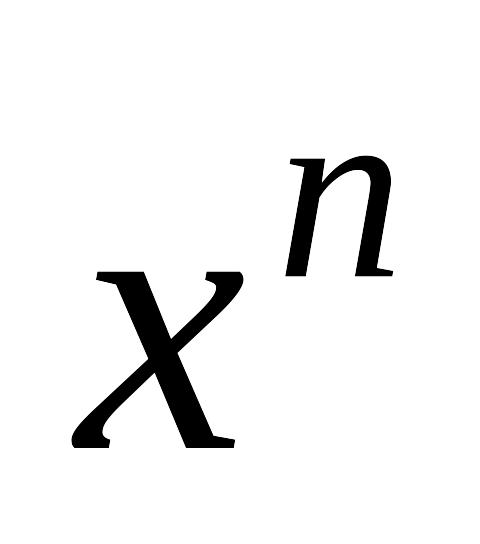 - вектор, полученный на n
– ой итерации.
- вектор, полученный на n
– ой итерации.Предполагается, что задано начальное приближение
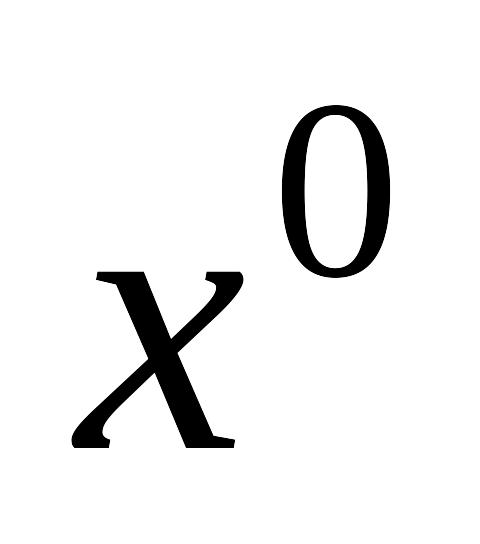 и существует
и существует
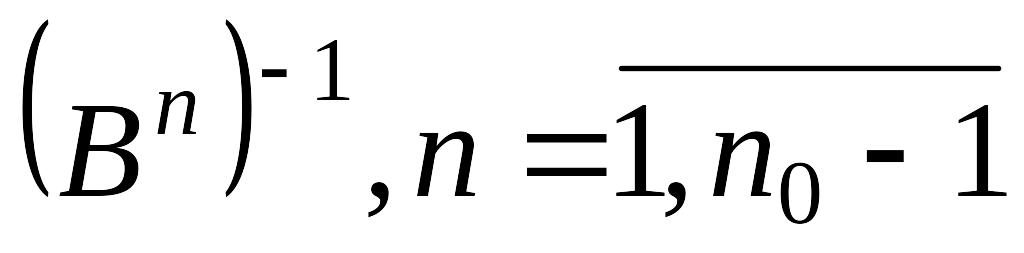 .
.Определение 3. Итерационный метод (3) называется явным, если
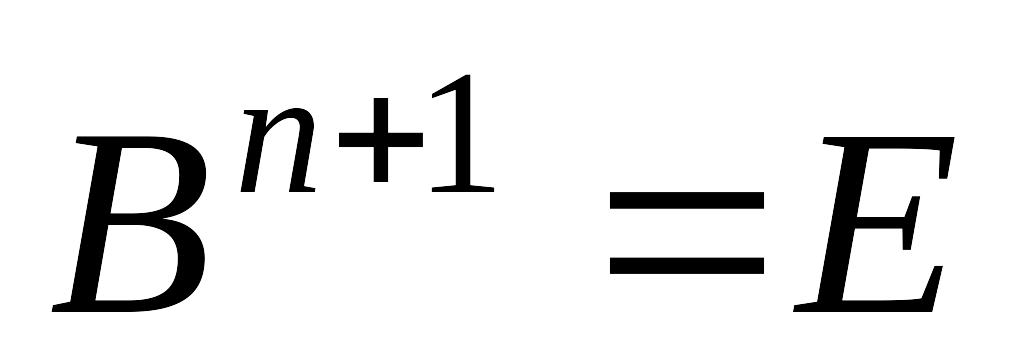 ,
неявным, если
,
неявным, если
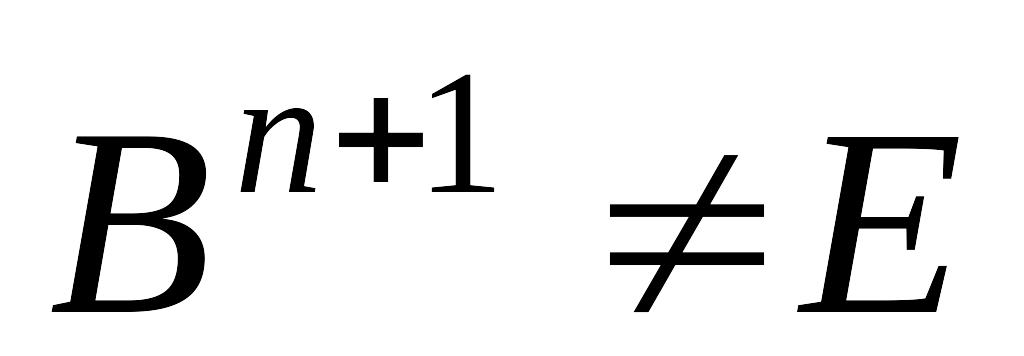 ,
где E – единичная
матрица.
,
где E – единичная
матрица.Определение 4. Итерационный метод (3) называется стационарным, если
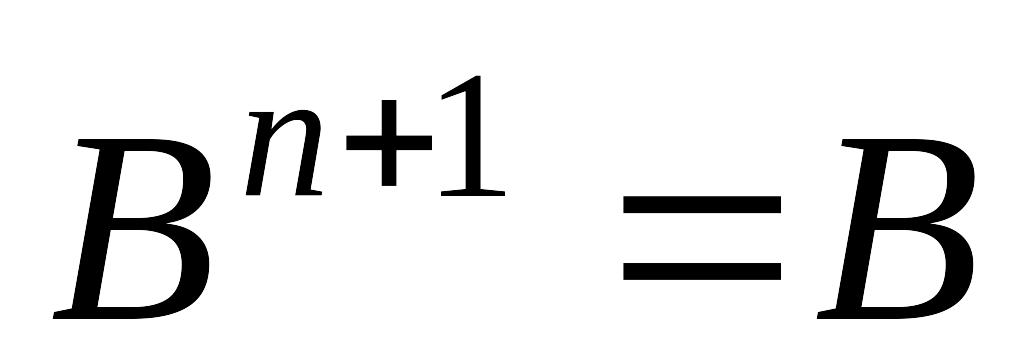 и
и
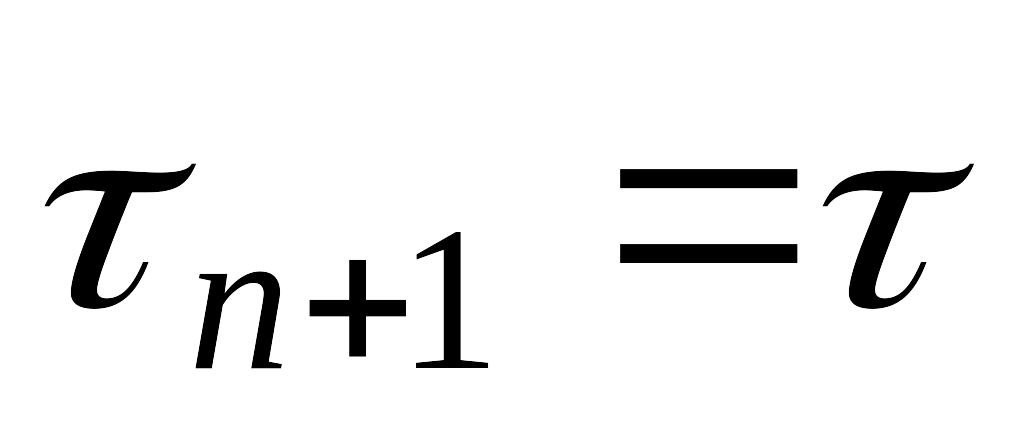 ,
т.е. не зависят от номера итерации, и
нестационарным – в противоположном
случае.
,
т.е. не зависят от номера итерации, и
нестационарным – в противоположном
случае.Определение 5. Матрица
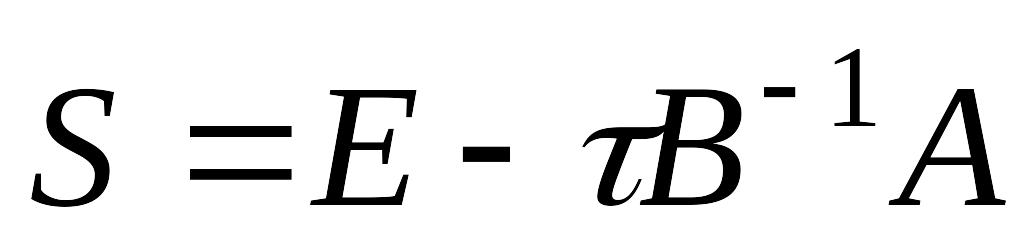 называется матрицей перехода от n-ой
итерации к (n+1)-ой.
называется матрицей перехода от n-ой
итерации к (n+1)-ой.Теорема 1. (Необходимое и достаточное условие сходимости)
Итерационный метод
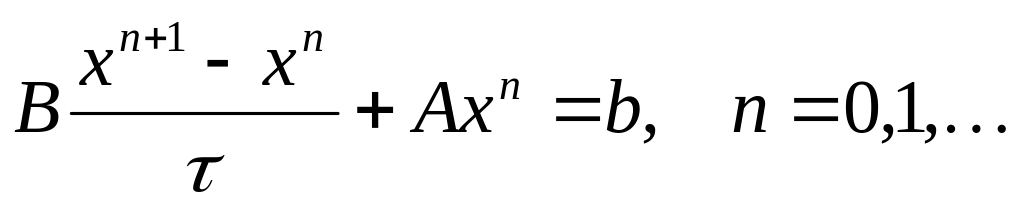 сходится при любом начальном
приближении, тогда и только тогда,
когда все собственные значения матрицы
перехода S по модулю
меньше единицы.
сходится при любом начальном
приближении, тогда и только тогда,
когда все собственные значения матрицы
перехода S по модулю
меньше единицы.Теорема 2. (Достаточное условие сходимости)
Итерационный метод сходится при любом начальном приближении, если норма матрицы перехода S меньше единицы.
