Глава 5. Тепловые процессы и аппараты

§ 5.1. Основы теплопередачи

Тепловыми называют процессы, скорость протекания которых определяется скоростью подвода или отвода теплоты.

Тепловая энергия передается от тел, имеющих более высокую температуру, телам с более низкой температурой. Совокупность значений температуры в данный момент для всех точек пространства называется температурным полем. Если температура зависит от времени, то температурное поле называется нестационарным, в противном случае поле стационарное.

Геометрическое место точек, имеющих одинаковую температуру, образует изотермическую поверхность.

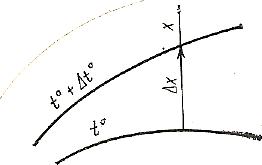" Если рассмотреть две изотермы (рис. 5.1) с температурой t° и t°+∆t° , то можно отметить, что наиболее резкое изменение темпе­ратуры наблюдается в направлении нормали к изотермическим поверхностям. Предел отношения разности температур к расстоянию между изотермами по нормали ∆x называется тем­пературным градиентом.

= dt°/dx = ◊t° , (5.1)

Где ◊t° -градиент температур.

Положительное направление градиента температур считается в сторону возрастания температуры.

Рис. 5.1 К объяснению Количество переносимой теплоты за единицу температурного градиента времени на­зывается тепловым потоком. Тепловой поток, отнесенный к единице поверхности, называется плотностью теплового потока. Направле­ние теплового потока противоположно направлению температурно­го градиента.

Различают три способа передачи теплоты: теплопроводность, конвекция и тепловое излучение.

Теплопроводность. Теплопроводность, или кондукция,— процесс распространения теплоты путем непосредственного соприкоснове­ния между частицами тела. Теплопроводностью передается теплота в газах, жидкостях и твердых телах.

Основной закон распространения теплоты теплопроводностью

q = -λ ◊t° , (5.2)

где q — плотность теплового потока; λ - коэффициент теплопровод­ности.

Соотношение (5.2) выражает основной закон теплопроводности Фурье. Знак минус в правой части уравнения показывает, что на­правления теплового потока и температурного градиента противо­положны. Коэффициент теплопроводности определяет собой коли­чество теплоты, которое проходит в единицу времени через единицу поверхности при разности температур в 1° на единицу длины. Ко­эффициент теплопроводности является физическим параметром ве­щества и зависит от свойств, тела: структуры, плотности, давления и температуры.

Общее количество теплоты Q, переданное теплопроводностью для стационарного температурного поля через плоскую стенку тол­щиной δ с поверхностью А за время t при разности температур на наружных поверхностях стенки ∆t° :

Q = qAt = 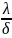∆t° At; (5.3)

то же, для плоской многослойной стенки

Q = qAt = At ,

Дифференциальное уравнение теплопроводности Фурье в непо­движной среде

, (5.4)

где а - коэффициент температуропроводности, a=λ / (cρ) ; ◊²t° - оператор Лапласа, ◊²t = d²t°/dx² + d²t°/dy² + d²t°/dz².

В частном случае при установившемся процессе температура не изменяется во времени и dt°/dt=0. При этом так как значение a не может быть равно нулю, то, следовательно, ◊²t° = 0 или

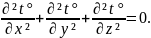(5.5)

Уравнение (5.5) является дифференциальным уравнением тепло­проводности в неподвижной среде при установившемся тепловом режиме.

Конвекция — процесс распространения теплоты перемещением частиц. Плотность теплового потока, передаваемого конвекцией, описывается уравнением Ньютона — Рихмана

q = α∆t°. (5.6)

Коэффициент теплоотдачи а показывает, какое количество теп­лоты отдается единицей поверхности в окружающую среду в еди­ницу времени при разности температур между теплоотдающим и тепловоспринимающим телом в 1°. На коэффициент теп­лоотдачи влияют: физические свойства жидкости или газа (вязкость, плотность, теплопроводность, теплоемкость); скорость дви­жения жидкости или газа (с увеличением скорости движения а возрастает); характер движения жидкости или газа — ламинарное или турбулентное; форма омываемой поверхности; степень шерохо­ватости поверхности и т. д.

Таким образом, коэффициент теплоотдачи в отличие от коэффи­циента теплопроводности не является физическим параметром жид­кости или газа.

При изучении конвективного теплообмена основной задачей яв­ляется определение коэффициента теплоотдачи. Определение его расчетными методами связано с большими трудностями, поэтому а находят обычно опытным путем.

Обычно а определяют через критерии подобия.

Уравнение (5.6) справедливо для стационарных режимов. В ин­женерной практике чаще приходится иметь дело с нестационарны­ми тепловыми процессами. Например, при тепловлажностной обра­ботке бетона в период подъема температуры количество теплоты, переданного поверхности изделия от паровоздушной среды, посто­янно изменяется, т. е. процесс конвективной передачи теплоты яв­ляется нестационарным.

Дифференциальное уравнение конвективного теплообмена (уравнение Фурье—Кирхгофа)

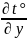vx + vy vz = a◊²t°. (5.7)

Для установившегося процесса член dt°/dt=0. Для твердых тел vx = vy = vz и уравнение превращается в дифференциальное уравнение теплопроводности.

Критерии теплового подобия можно получить, проведя подобные преобразования уравнения (5.7). В подобных преобразованиях зна­ки математических операторов могут быть отброшены, поэтому

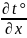( vx + vy vz ) ~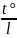 v; a◊²t° ~ ; ~ .

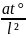Если в качестве масштаба сравнения принять количество теп­лоты, передаваемого, теплопроводностью, то, разделив член t°/t на at°/l² , получают безразмерный комплекс l²/(at). Обратную величи­ну этого комплекса называют критерием Фурье:

Fo = at/l². (5.8)

Необходимое условие подобия неустановившихся процессов теп­лообмена обеспечивается равенством критериев Фурье в сходствен­ных точках тепловых потоков. Этот критерий является аналогом критерия Но при гидродинамическом подобии.

Критерий Пекле, являющийся мерой соотношения конвективной и кондуктивной составляющих при конвективном теплообмене, по­лучают делением конвективного члена t°v/l на at°/l²:

Pе=v1/а. (5.9)

Умножив числитель и знаменатель критерия Ре на v, можно выразить его через критерии Рейнольдса и Прандтля:

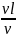
Pе = = (vlρ/η) (ηcp/λ) = Re Pr ,

откуда

Pr = ηcp/λ. (5.10)

Критерий Pr является мерой подобия полей температур и ско­ростей и характеризует подобие физических свойств теплоносите­лей при конвективном теплообмене. Передача теплоты в погранич­ном слое характеризуется уравнением: -λ ◊t° = α(t°ст –t°ж). Прове­дя подобные преобразования (отбросив знаки математических опе­раторов), получим –λ ◊t° ~ λ t°/l; α(t°ст –t°ж) = α∆t° ~ αt°, откуда критерий Нуссельта

Nu = αt° / (λt° / l) = αl / λ . (5.11)

Равенство критериев Нуссельта характеризует подобие процес­сов теплопереноса на границе между стенкой и потоком жидко­стей.

Поскольку искомый коэффициент теплоотдачи входит в крите­рий Нуссельта, он и является определяемым, т. е.

Nu = f΄΄(Fo , Pr , Re , Fr , Ho , Г) (5.12)

При вынужденном движении жидкости, когда влияние критерия Fr исчезающе мало, в установившемся процессе теплообмена (от­сутствие критериев Но и Fo) обобщенное уравнение принимает вид

Nu = ψ ( Re , Pr , Г). (5.13)

При естественной конвекции критерий Fr исключать нельзя. Вследствие трудностей при определении скорости движения жидко­сти при естественной конвекции последний обычно заменяют про­изводным критерием Архимеда, который равен

Ar = (gl³ / ν²) (∆ρ / ρ₀) (5.14)

Так как ∆ρ = ρ₀ - ρ₀ (1 - β∆t°) = ρ₀ β t° , то, подставляя в критерий Ar вместо ∆ρ его значение, получают критерий Грасгофа:

Gr = g l³ β ∆t° / ν², (5.15)

где l — определяющий геометрический размер (например, высота стенки); β — коэффициент объемного расширения жидкости; ∆t° — разность температур между жидкостью и стенкой.

Критерий Грасгофа есть мера отношения сил трения к подъем­ной силе.

Таким образом, при естественной конвекции или свободном дви­жении жидкости обобщенное уравнение имеет вид

Nu = Ф (Gr , Pr , Г ). (5.16)

Лучистый теплообмен - процесс распространения теплоты в виде электромагнитных волн. Часть тепловой энергии тела превращается в лучистую энергию и в виде электромагнитных колебаний рас­пространяется в пространстве со скоростью света. Встречая на сво­ем пути твердые, жидкие или газообразные тела, тепловые лучи частично поглощаются, частично отражаются и в некоторых слу­чаях частично проходят сквозь эти тела. Поглощенные лучи снова превращаются в тепловую энергию. Такое превращение энергии наблюдается непрерывно как для системы, в которой тела имеют различные температуры, так и для системы, где температура у всех тел одинакова. В этом случае количество излучаемой энергии равно поглощаемой, т. е. система находится в тепловом равновесии.

Общее количество теплоты, излучаемое поверхностью А в единицу времени, называют лучистым тепловым потоком Q. Величину лучистого теплового потока, отнесенную к единице поверхности, называют поверхностной плотностью лучистого теплового потока или лучеиспускательной способностью E=Q/A.

Количество теплоты, переданного лучистым теплообменом

q = αл ∆t, (5.17)

где αл — коэффициент теплообмена излучением,

αл = εп С₀ [ (T₁/100)⁴ - (T₂/100)⁴ ] / (T₁ - T₂), (5.18)

здесь εп — приведенная степень черноты излучаемого и восприни­маемого излучение тел; Со — коэффициент излучения абсолютно черного тела; Т₁ и Т₂ - абсолютные температуры тел.

В технике в передаче теплоты, как правило, участвуют одновре­менно два или все три способа передачи теплоты — теплопровод­ность, конвекция и излучение.

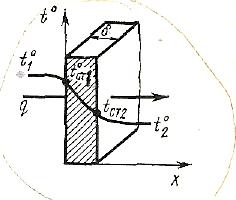Сложным теплообменом называют передачу теплоты одновре­менно несколькими способами. Теплообмен между горячей и хо­лодной средой через разделительную твердую стенку является од­ним из наиболее важных и часто используе­мых в промышленности строительных матери­алов. Например, в многочисленных теплообменных устройствах основным рабочим про­цессом является процесс теплообмена между теплоносителями. Такой теплообмен называ­ют теплопередачей. Рис.5.2 теплопередача через

плоскую однородную стену

Получим полный температурный на­пор t₁°-t₂° = q(1/α₁ + δ/λ + 1/α₂) , откуда определим значение плотности теплового потока

q = (t₁°-t₂°) / (1/α₁ + δ/λ + 1/α₂) (5.19)

Знаменатель равенства (5.19) представляет собой сумму терми­ческих сопротивлений, которая состоит из термического сопротивления теплопроводности δ/λ и двух термических сопротивлений теп­лоотдачи 1/α₁ и 1/α₂. Введем обозначение

К = 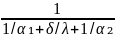. (5.20)

Из выражений (5.19) и (5.20) получим

q=K(t₁°-t₂°). (5.21)

Величину К называют коэффициентом теплопередачи [Вт/(м²·°С)], а величину, обратную коэффициенту теплопередачи, назы­вают полным термическим сопротивлением теплопередаче

R = 1/K = 1/α₁ + δ/λ + 1/α₂. (5.22)

В расчетах используют критерии Фурье — Fo = at/l² ; Био — Bi = al/λ ; геометрический критерий — Г = х/l , где х— расстояние от поверхности тела до расчетной точки; l — характеристический раз­мер тела (например, для шара — его радиус).

Критерий Био характеризует подобие процессов нестационарной теплопроводности и постоянство отношения внутреннего термиче­ского сопротивления теплопроводности к внешнему термическому сопротивлению теплоотдачи. Внешне он сходен с критерием Нус-сельта. Величина λ в критерии Bi в отличие от критерия Nu —ко­эффициент теплопроводности твердого тела ( в Nu — жидкости). Коэффициент теплоотдачи α в критерии Bi задается условиями однозначности.

Обычно в промышленности строительных материалов нестацио­нарный режим сводится к решению задач, связанных с установле­нием температуры в определенных точках тела в заданный момент времени, к определению длительности процесса нагрева или осты­вания тела, определению количества теплоты, полученного или от­данного телом в определенный промежуток времени.

Температуры поверхности (t°ст) и центра (tц°) стенки опреде­ляют по уравнениям:

θст/θ₀ = (t°ст - t°ср) / (t°₀ - t°ср) = f ( Bi, Fo); (5.24)

θц/θ₀ = (t°ц - t°ср) / (t°₀ - t°ср) = φ (Bi, Fo). (5.25)

Количество теплоты при нагреве или остывании стенки за время t вычисляют исходя из зависимости

θt /θ₀ = φ (Bi, Fo). (5.26)

В приведенных уравнениях θ = t°-t °ср - избыточная по отноше­нию к температуре среды температура поверхности (t°ст) или центра (t°ц) стенки в данный момент времени t; θ₀ = t°₀ - t°ср — избыточная температура поверхности или центра стенки в начальный момент времени, т. е. при t=0 и t° = t₀°; θ/θ₀ — безразмерная температура стенки, где θ — некоторая температура, принятая за масштаб темпе­ратур; θ₀ — внутренняя теплота стенки в начальный момент време­ни (за начало отсчета принята внутренняя теплота стенки при температуре, равной температуре окружающей среды).

Для определения t°ст , t°ц и θt сначала находят θст / θ₀ ; θц / θ₀ и θt /θ₀ по вычисленным критериям Bi и Fo, пользуясь графиками или таблицами, имеющимися в справочной литературе. Затем по фор­мулам (5.24...5.26) с известными начальными значениями t°₀ , t°ср и θ₀ вычисляют искомые величины.