
- •Допущения в сопротивлении материалов
- •Деформации: виды, определения
- •Метод сечений: определение внутренних сил
- •Напряжение: определение, виды
- •Условие прочности
- •Назначение и виды испытаний в сопромате. Диаграммы растяжения и сжатия
- •Влияние химического состава, температуры, термической обработки и скорости нагружения на механические свойства материалов
- •Коэффициент концентрации напряжений
- •Допускаемые напряжения. Коэффициент запаса прочности.
- •Расчеты на прочность при растяжении-сжатии (1 задание). Определение напряжения и деформации.
- •Связь между продольной и поперечной деформациями. (1 лабораторная)
- •Расчеты на прочность при чистом кручении. Деформация кручения, касательное напряжение.
- •Рациональные формы сечений при кручении.
- •Чистый и поперечный прямой изгиб.
- •Построение эпюр поперечных сил и изгибающих моментов при изгибе.
- •Деформация и нормальное напряжение при чистом изгибе.
- •Рациональные формы поперечных сечений балок при изгибе.
- •Гипотезы прочности. Третья гипотеза.
- •Расчет сжатых стержней на устойчивость – общее понятие.
- •Расчет на прочность при напряжениях, циклически изменяющихся во времени.
-
Коэффициент концентрации напряжений
Концентрацией называют явление скачкообразного увеличения напряжений вблизи резких смен формы детали, отверстий, выточек.
Мерой концентрации является теоретический коэффициент концентрации напряжений равный:
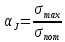 при растяжении, изгибе,
при растяжении, изгибе, 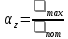 при кручении,
при кручении,
 — так называемое номинальное напряжение,
определяемое по формулам сопротивления
материалов,
— так называемое номинальное напряжение,
определяемое по формулам сопротивления
материалов, 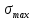 — наибольшее местное напряжение. Данные
о теоретическом коэффициенте концентрации
напряжений приводятся в справочниках
по машиностроению. Концентрация
напряжений оказывает на прочность
детали различное влияние в зависимости
от свойств материала и условий нагружения.
Поэтому вместо теоретического коэффициента
концентрации напряжения
— наибольшее местное напряжение. Данные
о теоретическом коэффициенте концентрации
напряжений приводятся в справочниках
по машиностроению. Концентрация
напряжений оказывает на прочность
детали различное влияние в зависимости
от свойств материала и условий нагружения.
Поэтому вместо теоретического коэффициента
концентрации напряжения 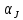 вводят эффективный коэффициент
концентрации напряжений
вводят эффективный коэффициент
концентрации напряжений 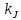 и
и 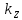 .
.
-
Допускаемые напряжения. Коэффициент запаса прочности.
Для того
чтобы конструкция была прочной, наибольшее
расчетное значение 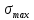 в
ней не должно превышать предельного:
в
ней не должно превышать предельного:
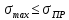
Это выражение
иногда называют физическим условием
прочности. Для надежной работы
конструкция должна обладать определенным
запасом надежности, запасом прочности,
т.к. фактические нагрузки и свойства
материала реально могут существенно
отличаться от принятых для расчета. При
этом все эти факторы, снижающие прочность
конструкции, носят случайный характер.
Следовательно, нельзя допускать чтобы
расчетное напряжение 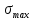 приближалось к предельному. Для
обеспечения надежности конструкции
вводят коэффициент запаса
прочности, равный отношению
предельного напряжения к расчетному
напряжению:
приближалось к предельному. Для
обеспечения надежности конструкции
вводят коэффициент запаса
прочности, равный отношению
предельного напряжения к расчетному
напряжению:
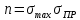
На основе
опыта проектирования и эксплуатации
устанавливают минимально необходимые
величины коэффициентов запаса прочности.
Эти величины
называют допускаемыми или нормативными коэффициентами
запаса и обозначают 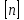 .
Расчетный запас прочности должен быть
не ниже допускаемого, т.е. условие
прочности принимает вид:
.
Расчетный запас прочности должен быть
не ниже допускаемого, т.е. условие
прочности принимает вид:
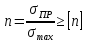
Перепишем выражение в виде
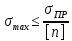 или
или
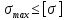
Это выражение называют: условием прочности по нормальным напряжениям.
Напряжение 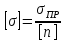 - допускаемое напряжение: напряжение
при котором обеспечивается безопасная
работа конструкции с надлежащим запасом
прочности.
- допускаемое напряжение: напряжение
при котором обеспечивается безопасная
работа конструкции с надлежащим запасом
прочности.
В машиностроении
на основании практики конструирования,
расчета и эксплуатации машин и сооружений
для пластичных материалов при статической
нагрузке принимают 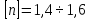 ;
для хрупких материалов
;
для хрупких материалов
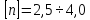
-
Расчеты на прочность при растяжении-сжатии (1 задание). Определение напряжения и деформации.
При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ. Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:
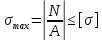
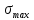 –
максимальные расчетные нормальные
напряжения в стержне,
N
– внутренние продольные силы (принимаются
с построенных эпюр),
А
– соответствующая площадь поперечного
сечения бруса,
–
максимальные расчетные нормальные
напряжения в стержне,
N
– внутренние продольные силы (принимаются
с построенных эпюр),
А
– соответствующая площадь поперечного
сечения бруса,
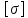 – допустимые напряжения (расчетное
сопротивление) для материала стержня.
– допустимые напряжения (расчетное
сопротивление) для материала стержня.
Данное условие означает что для того, чтобы стержень при растяжении-сжатии оставался прочным, напряжения σ в его сечениях не должны превышать допустимых значений [σ].
В случаях, когда для материала стержней допустимые напряжения на растяжение [σ]р и на сжатие [σ]сж отличаются, при сравнении необходимо учитывать знак напряжений σ, который зависит только от знака соответствующих внутренних сил N.
Так, положительные значения напряжений σ сравниваются с [σ]р, отрицательные напряжения по модулю не должны превышать значения [σ]сж.
Проверка на прочность
В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ, после чего максимальная из них сравнивается с заданным допустимым значением [σ].
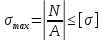
Ответ в данной задаче дается в виде заключения:
-
если
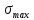 ≤
≤ 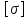 стержень прочный,
стержень прочный, -
если
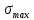 >
>
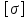 стержень непрочный.
стержень непрочный.
Подбор размеров сечения
По известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.
Для этого условие прочности записывается относительно искомой величины.
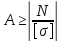
Полученные размеры в случае необходимости можно изменять под нагрузку. Уменьшение размеров приведет к повышению напряжениями допустимых значений и наоборот.
Определение грузоподъемности стержня
По известным
размерам и материалу можно рассчитать
величину допустимой внутренней силы,
которую может выдержать стержень,
оставаясь прочным.
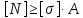
В данном случае условие прочности записано относительно внутренней силы N.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
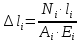
где N –
величина внутренней продольной силы,
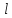 – длина рассматриваемого участка,
A
– площадь его поперечного сечения,
E
– модуль Юнга (продольной упругости)
для материала стержня
– длина рассматриваемого участка,
A
– площадь его поперечного сечения,
E
– модуль Юнга (продольной упругости)
для материала стержня
