
- •Учебная практика
- •По заправке оборудования (72 часа)
- •Задание
- •Бригаде уч-ся группы 361
- •Проверка правильности выбора сырья
- •Расчет вытяжки
- •Расчет крутки
- •Выбор и обоснование скоростных режимов
- •4 Выбор кпв. Расчет кро и ким
- •Расчет производительности
- •Методика определения степени разрыхления по массе клочков хлопкового волокна
- •Анализ отходов по переходам
- •Контроль качества прочеса на засоренность
- •Технологический расчет чесальной машины чм-50
- •Расчет общей и частной вытяжек и чисел зубьев вытяжной шестерни
- •Общая вытяжку можно найти исходя из утонения продукта на машине
- •Частная вытяжка между съемным барабаном 5 и питающим цилиндрами 1 рассчитывается по формуле
- •2. Определение числа зубьев ходовой шестерни и производительности машины
- •3. Определение частоты и скорости вращения рабочих органов
- •5. Определение времени наработки таза
- •Технологический контроль в чесальном цехе
- •Технологический расчет ленточной машины rsb – 951
- •Определение частных вытяжек и выбор параметров сменных элементов
- •2. Определение частоты вращения и окружных скоростей рабочих органов
- •3. Плановая производительность (кг/ч) одного выпуска ленточной машины определяется
- •4. Определение времени, необходимого для наработки одного таза.
- •Контроль качества ленты
- •Технологический расчет ровничной машины ра – 192
- •Определение диаметров сменных шкивов
- •Определение общей и частной вытяжек и числа зубьев вытяжных шестерен
- •Определение крутки ровницы и числа зубьев крутильной шестерни
- •Определение числа зубьев мотальной и подъемной шестерни
- •Определение числа зубьев механизма управления (замковых шестерен)
- •Частота вращения и окружные скорости рабочих органов
- •Определение производительности одного веретена
- •Определение массы ровницы на катушке и времени наработки съема
- •1.Расчет диаметра шкивов
- •2.Определение общей и частной вытяжек и числа зубьев вытяжных шестерен
- •3.Определение крутки пряжи и числа зубьев крутильной шестерни
- •4.Определение длины пряжи в слое и прослойке и числа зубьев мотальной шестерни и храповика
- •9.Максимальное натяжение пряжи в зоне «бегунок- початок».
- •Вычисление сводных характеристик результатов испытаний
- •Обработка результатов испытаний классическим способом
- •Нахождение границ классов
- •Литература
Обработка результатов испытаний классическим способом
Классический
способ является наиболее точным и его
можно применять при любом числе испытаний.
Допустим, что в результате n
измерений какого-либо свойства были
получены первичные данные
 ,
, ,
, …
… .
Необходимо определить среднее
арифметическое, среднее квадратичное
отклонение и коэффициент вариации.
.
Необходимо определить среднее
арифметическое, среднее квадратичное
отклонение и коэффициент вариации.
Среднее арифметическое вычисляется сложением всех первичных результатов испытаний и делением полученной суммы на число испытаний n:
 (38)
(38)
Среднее квадратичное отклонение вычисляют по формуле:
 (39)
(39)
где
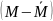 - отклонение каждого первичного результата
испытаний от среднего значения;
- отклонение каждого первичного результата
испытаний от среднего значения;
 0.005
0.005
Вычисляем коэффициент вариации
 =
=
Обработка результатов испытания способом произведений
При числе испытаний 50 и более ГОСТ 6611.1-73 предусматривает сокращение способы подсчета среднего арифметического, среднего квадратичного отклонения и коэффициента- способ сумм и способ произведений. Т.К. вычисление сводных характеристик классическим способом становится затруднительным с увеличением числа испытаний.
При использовании сокращенных способов обработки результатов испытаний составляют таблицы распределение первичных результатов испытаний по классам и проводят соответствующую обработку данных этой таблицы для установления сводных характеристик.
Порядок обработки результатов испытаний состоит из следующих этапов: нахождение границ классов. Разноска результатов испытаний по классам, вычисление сводных характеристик.
На примере данных полученных в результате 50 взвешиваний 100- метров пасм хлопчатобумажной пряжи линейной плотности 29 текс, рассмотрим порядок обработки испытаний способом сумм и способом произведений.
Нахождение границ классов
Классы представляют собой участки (численные интервалы) диапазона измеряемой свойства и служат для распределения результатов испытаний по группам.
 - сумма квадратов
отклонений первичных результатов
испытаний от среднего значения.
- сумма квадратов
отклонений первичных результатов
испытаний от среднего значения.
Коэффициент вариации (%) характеризует равномерность текстильного материала (рассчитывается до 0,01% и округляется до 0,1%) и вычисляется по формуле:

Таблица 21. Классический способ обработки результатов испытаний
Первичные результаты испытаний, %M |
Отклонение первичных результатов от среднего (M-M) |
Квадраты отклонений первичных результатов от среднего (M-M)2 |
1 |
2 |
3 |
5.84 5.83 5.83 5.93 5.92 5.93 5.84 5.88 5.84 5.87 5.87 5.90 5.93 5.95 5.94 5.82 5.83 5.85 5.92 5.88 5.88 5.76 5.73 5.73 5.82 5.84 5.80 5.84 5.86 5.87 5.93 5.91 5.90 5.87 5.88 5.81 5.84 5.84 5.85 5.91 5.84 5.87 5.91 5.90 5.90 5.81 5.79 5.80 5.76 5.91 |
-0.02 -0.03 -0.03 0.07 0.06 0.07 -0.02 0.02 -0.02 0.01 0.01 0.04 0.07 0.09 0.08 -0.04 -0.03 -0.01 0.06 0.02 0.02 -0.1 0.13 -0.13 -0.04 -0.02 -0.06 -0.020 0 0.01 0.07 0.05 0.04 0.01 0.02 -0.05 -0.02 -0.02 -0.01 -0.05 -0.02 0.01 0.05 0.04 0.04 -0.05 -0.07 -0.06 -0.1 0.05
|
0.0002 0.0009 0.0009 0.0049 0.0036 0.0049 0.0004 0.0004 0.0004 0.0001 0.0001 0.0016 0.0049 0.0081 0.0064 0.0016 0.0009 0.0001 0.0036 0.0004 0.0002 0.0001 0.0169 0.0169 0.0016 0.0004 0.0036 0.0004 0 0.0001 0.0049 0.0025 0.0016 0.0001 0.0004 0.0025 0.0004 0.0004 0.0001 0.0025 0.0004 0.0001 0.0025 0.0016 0.0016 0.0025 0.0049 0.0036 0.0001 0.0025 |
|
|
|
Рассмотрим классический способ обработки результатов определения неровноты ровницы 420 текс по трехсантиметровым отрезкам, проведенным в графе 1, табл.18.
 (40)
(40)
Определяем отклонение каждого первичного результата испытаний от среднего значения и заносим его в графу 2 таблицы 18. Алгебраическая сумма отклонений результатов должна ровняться нулю.
Находим величину квадрата каждого отклонения и записываем в графу 3 таблицы 18. Определяем сумму квадратов отклонений и по формуле вычисляем среднее квадратичное отклонение.
Каждый класс имеет нижнюю и верхнюю границы, т.е. предельные значения интервала.
Классы располагают столбцом от крайнего верхнего класса до крайнего нижнего класса в порядке возрастания числовых значений измеряемого свойства. Границы классов находят следующим образом.
Для рассматривания пример (число испытаний n=50) выбираем количество классов m=8
Мmax=5.93
Mmin=5.73
Определяем разность между R между наибольшими и наименьшими значениями:
R=Мmax-Mmin=5.93-5.73=0.2 (41)
Делим ее на количество классов:
К= =
=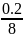 =0.025
(42)
=0.025
(42)
Вычисленную величину округляют в большую или меньшую сторону и принимают за классовый промежуток К.
Таблица 22. Обработка результатов испытаний способом произведений
Граница классов |
Отметка числа случаев |
Число случаев (частота y) |
Условное отклонение α |
yα |
yα2 |
1 |
2 |
3 |
4 |
5 |
6 |
5,72-5,74 5,75-5,77 5,78-5,80 5,81-5,83 5,84-5,86 5,87-5,89 5,90-5,92 5,93-5,95 |
|
2 2 3 7 10 9 9 6
|
-4 -3 -2 -1 0 1 2 3 |
-8 -6 -6 -6 0 9 18 18 S1=55 |
32 36 12 6 0 7 32 27 S2=152 |
S1=∑ yα=55
S2=∑ yα=152
Условное среднее значение определяют как полусумму значений нижних границ класса, которому соответствует нулевое условное отклонение и смежного класса, расположенного в порядке возрастания числовых значений:




 %
%
Таблица 23. Классический способ обработки результатов испытаний (Разрывная нагрузка)
Первичные результаты испытаний, % М |
Отклонение
первичных результатов от среднего
∑(М- |
Квадраты отклонений первичных результатов от среднего ∑(М- )2 |
1 |
2 |
3 |
700 695 770 770 750 710 705 670 717 800 685 700 645 730 800 650 745 695 745 780 630 750 700 790 795 775 660 710 675 670 615 680 625 650 690 640 630 675 710 655 730 680 770 700 650 715 655 705 685 640 |
-2 -7 50 50 30 -10 -15 -50 -3 80 -35 -20 -75 10 80 -70 25 -25 25 60 -90 30 -20 70 75 55 -60 -10 -45 -50 -105 -40 -95 -70 -30 -80 -90 -45 -10 -65 10 -40 50 -20 -70 -5 -65 -15 -35 -80
|
-4 -49 2500 2500 900 -100 -225 -2500 -9 6400 -1225 -400 -5625 100 6400 4900 625 -625 625 3600 -8100 900 -400 4900 5625 3025 -3600 -100 -2025 -2500 -11025 -1600 -9025 -4900 -900 -6400 -8100 -2025 -100 -4225 100 -1600 2500 -400 -4900 -25 -4225 -225 -1225 -6400
|
Mmax = 800
Mmin = 615
Определяем разность R между наибольшим и наименьшим значением:

Делим ее на количество классов m:

Таблица 22. Обработка результатов испытаний способом произведений (Разрывная нагрузка)
Граница классов |
Отметка числа случаев |
Число случаев (частота y) |
Условное отклонение α |
yα |
yα2 |
1 |
2 |
3 |
4 |
5 |
6 |
615-639 640-664 665-689 690-714 715-739 740-764 765-786 790-814 815-839 |
|
3 7 8 12 4 4 6 3 0
|
-3 -2 -1 0 1 2 3 4 5
|
-9 -14 -8 0 4 8 18 12 0 S1=29 |
27 28 8 0 4 16 54 19 0 S2=146 |
Таблица 24. Классический способ обработки результатов испытаний (Крутка)
Первичные результаты испытаний, % М |
Отклонение первичных результатов от среднего ∑(М- ) |
Квадраты отклонений первичных результатов от среднего ∑(М- )2 |
1 |
2 |
3 |
89 94 94 98 98 97 100 106 99 80 100 99 97 98 100 102 99 106 109 98 103 90 89 89 103 93 93 99 101 100
|
-8 -3 -3 1 1 0 3 9 2 -17 3 2 0 1 3 5 2 9 12 1 6 -7 -8 -8 6 -4 -4 2 4 3
|
64 9 9 1 1 0 9 81 4 289 9 4 0 1 9 25 4 81 144 1 36 49 64 64 36 16 16 4 16 9 |



 2=0,2688
2=0,2688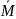 )
)