2.1.12 Потенциальные векторные поля. Критерии потенциального векторного поля

Потенциальные векторные поля

Пусть дана область в пространстве , и – векторное поле.

Определение. Векторное поле называется потенциальным в области , если существует функция такая, что

, , ,

при этом называют потенциалом векторного поля .

Теорема (характеризация потенциальных полей). Рассмотрим векторное поле в некоторой области . Следующие три условия эквивалентны:

1. Поле 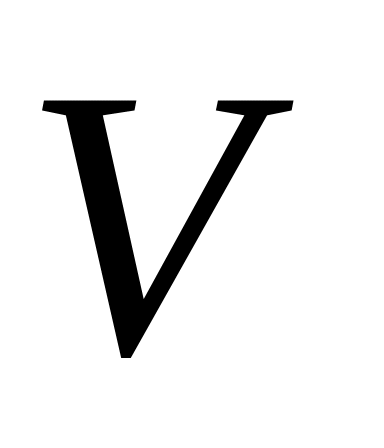потенциально.

2. Интеграл от поля вдоль ориентированной кривой не зависит от начальной и конечной точек этой кривой.

3. Интеграл от векторного поля по любой замкнутой кривой равен нулю.

Пример 2.1.12.1. Показать, что поле является потенциальным, и найти потенциал этого поля.

Решение.

Данное векторное поле определено на всей плоскости , являющейся односвязной областью. Покажем, что , т.е. что поле безвихревое, а следовательно, и потенциальное. Действительно, так как

, , , то

.

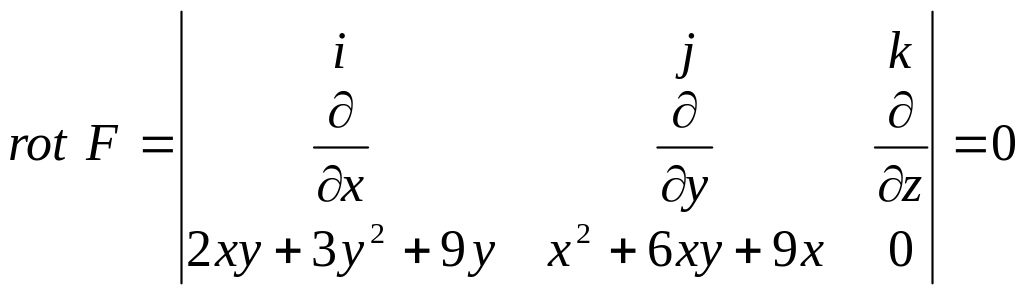Потенциал вычислим по формуле

,

т.е. .

Здесь в качестве начальной точки взята точка .

2.1.13 Формула Грина

Теорема (формула Грина). Пусть в области задано гладкое векторное поле , также задано множество в с кусочно-гладкой границей, которая правильно ориентирована, тогда справедлива следующая формула:

,

где , – координаты векторного поля.

Пример 2.1.13.1. Применяя формулу Грина, вычислить

, если – контур треугольника с вершинами , , , пробегаемый против хода часовой стрелки. Проверить результат непосредственным интегрированием.

Решение.

, . Находим . Таким образом,

, где область – треугольник . Уравнение прямой , уравнение . Вычислим двойной интеграл по данной области:

.

Вычислим теперь непосредственно криволинейный интеграл по контуру , состоящему из звеньев , , :

.

Уравнение ; следовательно , .

Уравнение ; следовательно , .

Уравнение ; значит , .

Таким образом,

.

Пример 2.1.13.2. Применяя формулу Грина, вычислить , где – окружность , пробегая против хода часовой стрелки.

Решение.

Здесь , . Тогда . Следовательно,

.

2.1.14 Формула Гаусса–Остроградского

Поверхностные интегралы

Р ассмотрим открытое множество , точки которого будем обозначать . Пусть – дифференцируемая функция, .

О браз отображения представляет собой при некоторых дополнительных предположениях двухмерную поверхность в .

Рассмотрим векторы

;

.

Они будут касательными к поверхности в текущей точке.

Потребуем, чтобы матрица, состоящая из векторов и , имела ранг 2. Тогда – элемент площади поверхности, – единичные нормали в текущей точке поверхности.

Определение. Поверхность ориентируема, если в каждой точке поверхности можно определить нормаль так, чтобы нормали непрерывно изменялись от точки к точке. Такую поверхность также называют двухсторонней.

Формула Гаусса–Остроградского

П усть в пространстве дана гладкая двусторонняя поверхность без края, ограничивающая область ,

Выберем в каждой точке нормаль , которая смотрит во внешность относительно . Таким образом, на задается ориентация.

Пусть задано векторное поле , которое определено в окрестности замыкания .

Определение. Дивергенцией гладкого векторного поля называется следующая функция:

.

Теорема (Формула Гаусса–Остроградского). В условиях, приведенных выше, справедлива следующая формула:

.

П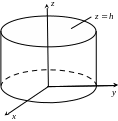 ример 2.1.14.1. По формуле Гаусса–Остроградского вычислить поверхностный интеграл , где – полная поверхность цилиндра , .

Решение.

Определяем , , . Затем находим производные , , . По формуле Гаусса–Остроградского вместо исходного поверхностного интеграла по замкнутой поверхности получим тройной интеграл по области , ограниченной этой поверхностью:

.

Переходя к цилиндрическим координатам, найдем

.