2.2.16 Методы решения нелинейных уравнений

Пусть дано нелинейное уравнение где – нелинейная функция, определена и непрерывна на некотором промежутке . Требуется найти корни уравнения.

Решение осуществляется в два этапа:

I. Отделение корней, нахождение отрезков , внутри которых содержится один простой или кратный корень.

Если функция определена, непрерывна на отрезке , и имеет конечную производную, причем на концах отрезка значения функции имеют разные знаки ( ), и ее первая производная сохраняет знак внутри отрезка , тогда на находится только один корень на , удовлетворяющий уравнению .

Графический способ отделения корней – построение графика функции применяется наиболее часто, но не обладает большой точностью. Часто бывает удобно заменить уравнение на равносильное , с формированием простых функций и и дальнейшим построением графиков этих функций. Корнями уравнения являются абсциссы точек пересечения графиков и .

Пример 2.2.16.1. Задано уравнение , отделить корень уравнения.

Решение.

Представим данное уравнение в виде и построим графики функций и . Абсцисса точки пересечения этих графиков находится в промежутке (рис. 16.1), поэтому начальное значение принадлежит этому отрезку.

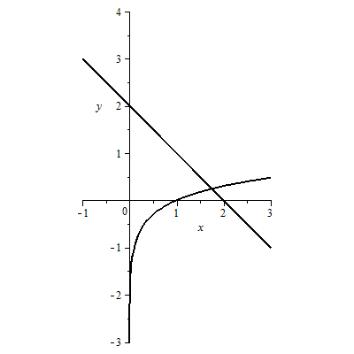
Рис. 16.1

Пример 2.2.16.2. Задано уравнение , отделить корень уравнения.

Решение.

Графический способ:

,

.

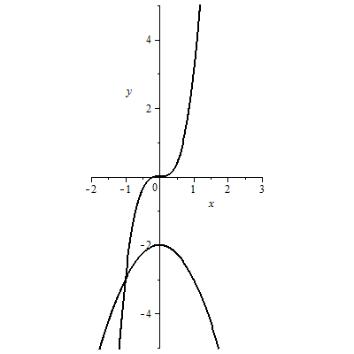
Ответ: .

Аналитический способ – построение графика функции на основе исследования функции выделить интервал, на котором лежит один корень.

II. Уточняется начальное значение корня уравнения, выбранного из , до заданной точности одним из численных методов, в котором реализуются последовательные приближения.

Пример 2.2.16.3. Задано уравнение , отделить корень уравнения.

Решение.

Аналитический способ решения:

,

,

.

,

.

,

.

						0
	+	0	–		–	0	+
	–		–	0	+		+
				т.перегиба

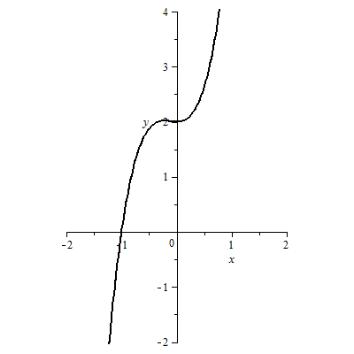
Ответ: .

Метод половинного деления

Пусть дано нелинейное уравнение и отделен простой корень на отрезке , выполняется условие и , и сохраняет знак. Требуется уточнить местоположение корня уравнения с заданной точностью .

Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция принимает различные знаки.

Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.

Метод имеет линейную, но безусловную сходимость, его погрешность за каждую итерацию уменьшается в 2 раза:

.