
- •1 Программа государственных экзаменов 5
- •2 Методические указания по вопросам программы 7
- •Введение
- •1 Программа государственных экзаменов Математический анализ
- •Математическое моделирование, математическое программирование, теория игр, численные методы
- •2 Методические указания по вопросам программы
- •2.1 Математический анализ
- •2.1.1 Теоремы Вейерштрасса
- •2.1.2 Теоремы Роля, Лагранжа
- •2.1.3 Теоремы Коши, Ферма
- •2.1.4 Формула Тейлора
- •2.1.5 Длина гладкой кривой
- •2.1.6 Объем тела вращения
- •2.1.7 Площадь поверхности тела вращения
- •2.1.8 Понятие компакта
- •2.1.9 Необходимые и достаточные условия локальных экстремумов
- •2.1.10 Задачи на относительный экстремум. Правило множителей Лагранжа
- •2.1.11 Теорема о замене переменных в кратных интегралах. Полярные, цилиндрические и сферические системы координат. Геометрический смысл Якобиана
- •2.1.12 Потенциальные векторные поля. Критерии потенциального векторного поля
- •2.1.13 Формула Грина
- •2.1.14 Формула Гаусса–Остроградского
- •2.1.15 Формула Стокса
- •2.2 Математическое моделирование, математическое программирование, теория игр, численные методы
- •2.2.1 Регрессионная модель. Однофакторная модель (построение модели, определение дисперсии, проверка адекватности)
- •2.2.2 Двойственная задача линейного программирования
- •2.2.3 Производственная функция Кобба-Дугласа. Коэффициенты эластичности
- •2.2.4 Модели расчета годовой производственной программы. Критерии в моделях
- •2.2.5 Модель оптимальной загрузки оборудования для выпуска комплектной продукции. Виды комплектов
- •2.2.6 Математическая обработка результатов опытов в планировании эксперимента. Полный факторный эксперимент. Свойства матрицы планирования
- •2.2.7 Управление запасами материалов. Типы моделей. Простейшая модель Уилсона
- •2.2.8 Сетевые графики. Критический путь. Оптимизация графика по времени в зависимости от вложенных средств
- •2.2.9 Сетевые графики. Вероятностная сеть. Оценка времени выполнения работ
- •2.2.10 Динамическое программирование. Распределение ресурсов между предприятиями головной фирмы
- •2.2.11 Задачи раскроя материалов и составления смеси. Область применения
- •2.2.12 Транспортная задача. Закрытая транспортная задача
- •2.2.13 Открытая транспортная задача
- •2.2.14 Матричные игры. Игры и
- •2.2.15 Матричные игры и линейное программирование
- •2.2.16 Методы решения нелинейных уравнений
- •Методика решения нелинейного уравнения методом половинного деления
- •Методика решения нелинейных уравнений методом Ньютона
- •Методика решения нелинейных уравнений методом простой итерации
- •2.2.17 Методы решения систем линейных уравнений
- •Методика решения систем линейных уравнений методом простой итерации
- •2.2.18 Нахождение наибольшего по модулю собственного числа матрицы
- •Методика решения задачи нахождения наибольшего собственного значения матрицы
- •2.2.19 Полиномиальное интерполирование
- •2.2.20 Метод наименьших квадратов
- •Применение степенных функций в методе наименьших квадратов
- •Методика решения задачи сглаживания
- •2.2.21 Численное интегрирование
- •Список литературы
1 Программа государственных экзаменов Математический анализ
Теоремы Вейерштрасса.
Теоремы Роля, Лагранжа.
Теоремы Коши, Ферма.
Формула Тейлора.
Длина гладкой кривой.
Объем тела вращения.
Площадь поверхности тела вращения.
Понятие компакта.
Необходимые и достаточные условия локальных экстремумов.
Задачи на относительный экстремум. правило множителей Лагранжа.
Теорема о замене переменных в кратных интегралах. Полярные, цилиндрические и сферические системы координат. Геометрический смысл Якобиана.
Потенциальные векторные поля. Критерии потенциального векторного поля.
Формула Грина.
Формула Гаусса–Остроградского.
Формула Стокса.
Математическое моделирование, математическое программирование, теория игр, численные методы
Регрессионная модель. Однофакторная модель (построение модели, определение дисперсии, проверка адекватности).
Двойственная задача линейного программирования.
Производственная функция Кобба-Дугласа. Коэффициенты эластичности.
Модели расчета годовой производственной программы. Критерии в моделях.
Модель оптимальной загрузки оборудования для выпуска комплектной продукции. Виды комплектов.
Математическая обработка результатов опытов в планировании эксперимента. Полный факторный эксперимент. Свойства матрицы планирования.
Управление запасами материалов. Типы моделей. Простейшая модель Уилсона.
Сетевые графики. Критический путь. Оптимизация графика по времени в зависимости от вложенных средств.
Сетевые графики. Вероятностная сеть. Оценка времени выполнения работ.
Динамическое программирование. Распределение ресурсов между предприятиями головной фирмы.
Задачи раскроя материалов и составления смеси. Область применения.
Транспортная задача. Закрытая транспортная задача.
Открытая транспортная задача.
Матричные игры. Игры
 и
и
 .
.Матричные игры
 и линейное программирование.
и линейное программирование.Методы решения нелинейных уравнений.
Методы решения систем линейных уравнений.
Нахождение наибольшего по модулю собственного числа матрицы.
Полиномиальное интерполирование.
Метод наименьших квадратов.
Численное интегрирование.
2 Методические указания по вопросам программы
2.1 Математический анализ
2.1.1 Теоремы Вейерштрасса
Функции, непрерывные на отрезке
Рассмотрим
числовую функцию
![]() ,
заданную на отрезке
,
заданную на отрезке
![]() .
Будем говорить, что она непрерывна
на этом отрезке, если она непрерывна в
каждой точке из области определения
(на концах отрезка требуется односторонняя
непрерывность).
.
Будем говорить, что она непрерывна
на этом отрезке, если она непрерывна в
каждой точке из области определения
(на концах отрезка требуется односторонняя
непрерывность).
Отметим некоторые специфические свойства непрерывных функций на отрезке.
Теорема
(первая теорема Вейерштрасса). Если
функция
непрерывна на отрезке
![]() ,
то она ограничена на нем.
,
то она ограничена на нем.
Теорема
(вторая теорема Вейерштрасса). Если
функция
непрерывна на отрезке
,
то она достигает своих наибольшего и
наименьшего значений на нем, т.е.
существуют точки
![]() и
и
![]() на отрезке
такие, что для любого
на отрезке
такие, что для любого
![]() справедливо неравенство
справедливо неравенство
![]() .
.
П
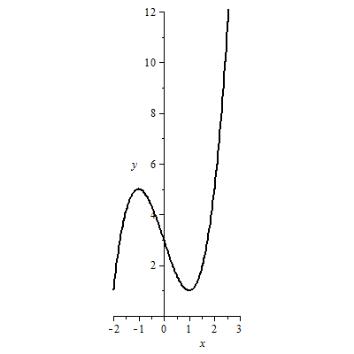 ример
2.1.1.1.
Найти
наибольшее и наименьшее значения функции
ример
2.1.1.1.
Найти
наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке
![]() .
.
Решение.
Так
как
![]() ,
то критическими точками функции являются
,
то критическими точками функции являются
![]() и
и
![]() .
Сравниваем значения функции в этих
точках и значения функции на концах
заданного отрезка:
.
Сравниваем значения функции в этих
точках и значения функции на концах
заданного отрезка:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отсюда
наименьшее значение функции
![]() достигается в точке
достигается в точке
![]() (в точке минимума), а наибольшее
(в точке минимума), а наибольшее
![]() достигается в точке
достигается в точке
![]() (на правом конце отрезка).
(на правом конце отрезка).
